B-деревья: добавление ключей

Операция добавления ключей в В-дерево начинается с выполнения операции поиска, когда аргумент поиска равен значению нового ключа. Если ключ действительно новый, то поиск завершится неудачно обнаружением некоторой вершины-листа. При этом возможны 4 случая:

1. В вершине-листе есть место для нового ключевого значения. Новый ключ помещается в соответствующее место этой вершины.

2. Вершина-лист содержит 2k ключей. В этом случае ее необходимо разделить на две вершины, каждая из которых содержит k ключей. После добавления нового ключа всего ключей станет 2k+1, но один из них должен быть включен в вершину-предшественник разделяемой вершины, которая является неполной.

3. Вершина-предшественник также является полной. В этом случае она также делится на две и этот процесс деления вершин может распространяться на все вершины вплоть до корня, при этом высота дерева увеличивается на единицу.

4. Вместо разделения заполненной вершины с целью добавления нового ключа можно проанализировать правую подобную ей вершину на наличие в ней свободного места. Если свободное место имеется, то последний ключ из заполненной вершины (после добавления в нее нового ключа) вытесняется в вершину-предшественник, а ключ из вершины-предшественника в свою очередь вытесняется на первую позицию правой подобной вершины со сдвигом ее содержимого вправо. При этом сохраняется и упорядоченность вершин, и приблизительно одинаковая степень их полезного использования.

Примеры добавления ключей для случаев 1-3 приведены на рис. 2.11, а для случая 4 – на рис. 2.12.

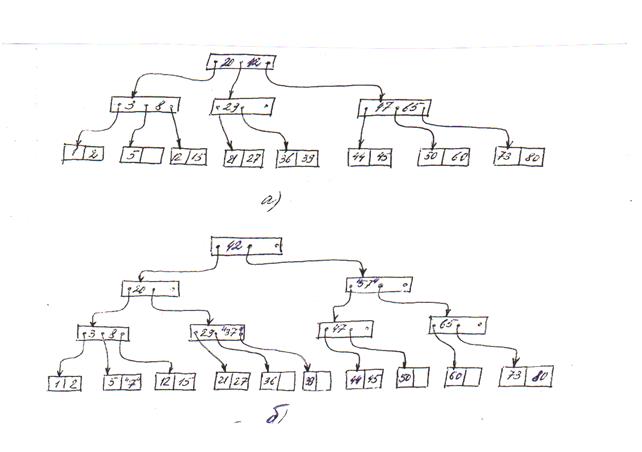
Рис.2.11

а) до добавления ключей 7, 37, 57;

б) после добавления.

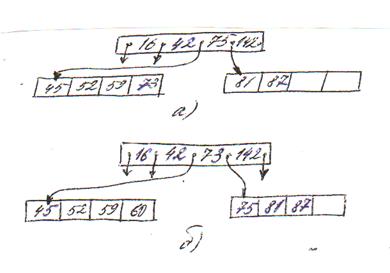
Рис. 2.12

а) до добавления ключа 60;

б) после добавления.