Поиск по бинарному дереву

При рассмотрении двоичного поиска бинарное дерево было использовано для пояснения работы алгоритма. Поиск можно организовать на основе явного использования бинарного дерева. Такой метод имеет два важных преимущества:

позволяет достичь минимума среднего числа сравнений в условиях неравновероятных запросов;

позволяет легко осуществлять поиск в часто изменяющихся (динамических) таблицах или файлах, не производя сортировку после каждого добавления записей.

Для реализации бинарного дерева в явном виде в каждой записи таблицы помимо поля ключа предусматривается два поля указателей U_R и U_L, в которых записываются адреса правого и левого преемников вершины дерева, соответствующей данной записи. Для свободных вершин, не имеющих преемников, в указателях помещается специальный символ «T» (тупик). Чтобы иметь возможность начать поиск, требуется адрес записи, соответствующей корню дерева: будем хранить его в специальной ячейке V. Пример явного задания бинарного дерева приведен на рис. 2.6.

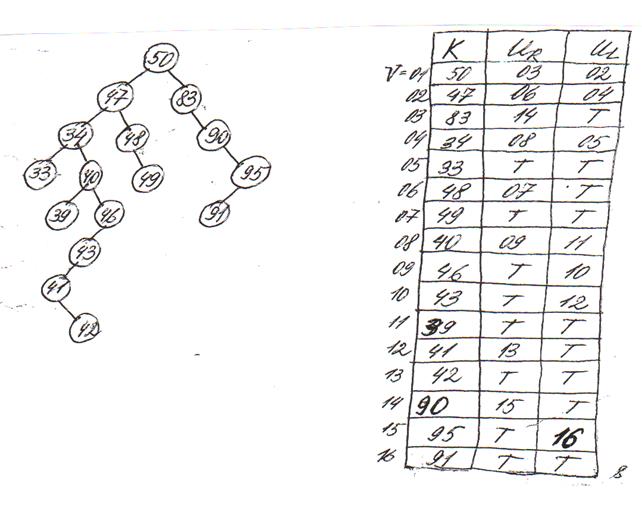
Рис.2.6

Явное задание бинарного дерева поиска

На каждом i-м шаге алгоритма поиска по бинарному дереву производится чтение из таблицы некоторой записи с ключом K_i и указателями Uⁱ_R и Uⁱ_L . При этом первый шаг всегда начинается с корня дерева, адрес которого содержится в указателе V.

На каждом шаге ключ K_i сравнивается с аргументом поиска A и по результатам сравнения выполняются следующие действия:

а) A= K_i – запись найдена, поиск заканчивается удачно;

б) A> K_i, Uⁱ_R =T или A< K_i, Uⁱ_L =T – тупик, запись в таблице отсутствует, поиск заканчивается неудачно;

в) A> K_i, Uⁱ_R ≠T – поиск продолжается, считывается очередная запись (K_i+1, Uⁱ⁺¹_R, Uⁱ⁺¹_L) по указателю Uⁱ_R;

г) A< K_i, Uⁱ_L ≠T – поиск продолжается, считывается очередная запись (K_i+1, Uⁱ⁺¹_R, Uⁱ⁺¹_L) по указателю Uⁱ_L.

При продолжении поиска (случаи в и г) аналогичным образом выполняется (i+1)-й шаг для записи K_i+1, полученной на i-м шаге.

Конкретный вид бинарного дерева для заданного множества записей определяется порядком, в котором записи заносятся в таблицу. Например, оно может выродиться в цепочку (линейный список) или принять сбалансированный вид, когда свободные вершины находятся на примерно одинаковом расстоянии от корня (см. рис. 2.7).

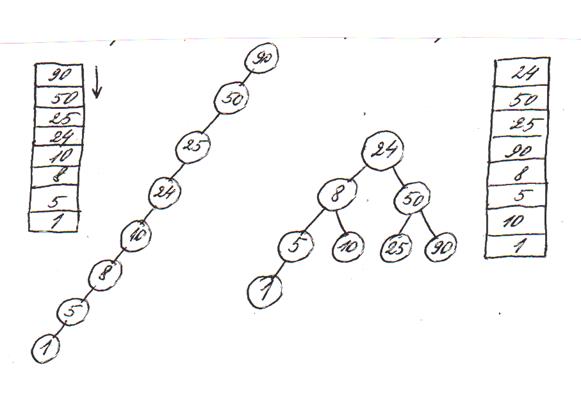
Рис.2.7

Возможные варианты бинарного дерева

В первом случае на рис. 2.7 поиск по бинарному дереву соответствует последовательному поиску, во втором – двоичному. Следовательно, необходимое число сравнений определяется видом бинарного дерева. Например, при равновероятных запросах и удачном поиске среднее число сравнений меняется примерно от log₂N-1 (двоичный поиск) и до N/2 (последовательный поиск). Если записи добавляются в таблицу в случайном порядке с одинаковыми вероятностями (что часто встречается на практике), то получаются бинарные деревья, для которых среднее число сравнений приблизительно равно 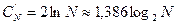. Это несколько больше, чем для двоичного поиска, но существенно меньше (особенно при больших N), чем для последовательного поиска.

Как уже отмечалось, метод бинарного дерева широко применяется для организации поиска в динамических таблицах, поскольку при его использовании не требуется сортировка записей таблицы. При добавлении новой записи ее просто помещают в конец таблицы и корректируют указатели некоторой старой записи, чтобы присоединить к бинарному дереву новую вершину. При этом, чтобы найти вершину для присоединения новой записи, достаточно проследить в дереве путь неудачного поиска для аргумента, равного ключу добавляемой записи. В связи с этим, большинство практических алгоритмов совмещают в себе операции поиска с операциями добавления новой записи в случае неудачного поиска. Несколько сложнее, но также вполне реализуема процедура удаления какой-либо записи из таблицы.

Недостатком поиска по бинарному дереву является дополнительный расход памяти в каждой записи на хранение указателей правого и левого преемников.