Чистый бинарный поиск

Поиск данного вида представляет собой обобщение двоичного поиска. Сформулируем задачу чистого бинарного поиска следующим образом.

Имеется таблица из N записей и задан некоторый аргумент поиска, причем заранее известно, что в таблице существует запись с ключом, равным аргументу поиска. Каждая запись таблицы имеет известную вероятность выбора p_i и выполняется условие нормировки 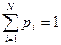. Поиск осуществляется следующим образом. На каждом шаге выбирается некоторое подмножество записей и выясняется, принадлежит или нет искомая запись выделенному подмножеству. Необходимо построить алгоритм, состоящий из подобных шагов и решающий любую задачу поиска при минимуме среднего числа сравнений. Каждое сравнение при этом делит текущее подмножество непроверенных записей на два других подмножества, одно из которых будет проверяться на данном шаге, а другое – нет.

Для построения такого алгоритма предположим, что записи упорядочены по возрастанию значений p_i и разобьем каждое из множеств непроверенных записей посередине (если число записей в множестве нечетно, то для определенности будем относить серединную запись к подмножеству с меньшими значениями p_i). Пример такого разбиения приведен на рис. 2.8.

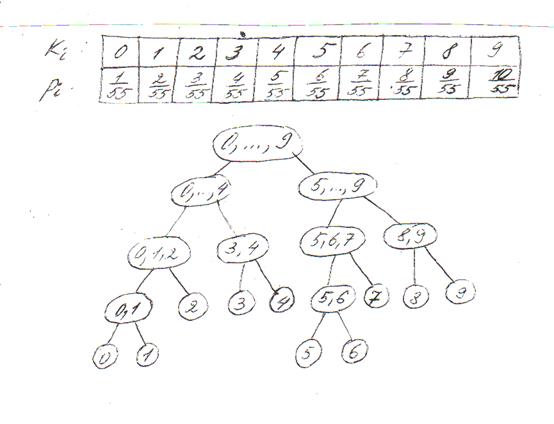
Рис.2.8. Пример чистого бинарного поиска

Для приведенного примера на первом шаге алгоритма выясняется, «равен ли аргумент поиска пяти или больше», т.е. производится первое сравнение. Пусть ответом на поставленный вопрос будет «нет», тогда следующим вопросом (второе сравнение) будет: «тройка или четверка?» и т.д.

Прямой подсчет среднего числа сравнений для рассмотренного примера дает: C₁₀’=4∙(1/55 + 2/55) + 3∙(3/55 + 4/55 + 5/55) + 4∙(6/55 + 7/55) + 3∙(8/55 + 9/55 + 10/55) = 3,291.

Рассмотренная задача соответствует удачному поиску. Однако, если сравнить этот алгоритм с алгоритмом двоичного поиска, то легко заметить, что его поведение в точности соответствует случаю неудачного двоичного поиска.

Сравнивая задачу чистого бинарного поиска с рассмотренной в разделе 1 задачей экономного кодирования, легко убедиться, что они идентичны. Дерево поиска соответствует при этом бинарному кодовому дереву. Следовательно, для улучшения алгоритма чистого бинарного поиска можно воспользоваться процедурами экономного кодирования (Шеннона-Фано или Хафмана). Так, применение этих процедур к рассматриваемому примеру обеспечивает среднее число сравнений, равное 3,145. При этом, ввиду оптимальности процедуры Хафмана, это число не может быть меньше.