Последовательный поиск

Этот вид поиска является единственно возможным для последовательных ЗУ, однако ввиду своей простоты и универсальности он часто применяется и для адресных ЗУ.

Алгоритм последовательного поиска заключается в следующем: на каждом шаге считывается очередная запись и ее ключ сравнивается с аргументом поиска. Шаги повторяются, начиная с первой записи таблицы, до тех пор, пока либо ключ очередной записи не совпадет с аргументом поиска, либо не будут считаны все записи таблицы. В первом случае поиск заканчивается удачно, во втором – неудачно.

В случае удачного поиска возможное число сравнений лежит в пределах [1,N], где N – число записей в таблице. Для случая неудачного поиска всегда требуется N сравнений.

Пусть значения аргумента случайны, т.е. в текущем запросе с некоторой вероятностью Q аргумент не совпадает ни с одним ключом таблицы, а с вероятностью 1-Q совпадает хотя бы с одним ключом (Q – вероятность неудачного поиска). Кроме того, в случае удачного поиска существуют вероятности p_i того, что аргумент совпадает с ключом i-й записи таблицы ( 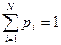). Тогда среднее число сравнений в случае удачного поиска составляет

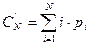
Для равновероятных запросов ,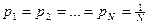

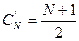
Среднее число сравнений с учетом как удачного, так и неудачного поиска составляет

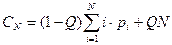
Для равновероятных запросов аргумента последняя формула принимает вид:

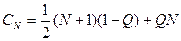
Пусть записи в файле или таблице упорядочены по возрастанию ключей, т.е. K₁<K₂<…<K_N. Во многих случаях упорядочивание файла легко производится с помощью разнообразных алгоритмов сортировки. Для удачного поиска предварительное упорядочивание файла никак не влияет на необходимое среднее число сравнений, однако в случае неудачного поиска это часто позволяет завершить поиск раньше, чем будет просмотрен весь файл. Действительно, лишь только ключ очередной записи превзойдет аргумент поиска, можно будет утверждать, что требуемая запись в таблице отсутствует. Таким образом, необходимое число сравнений в этом случае лежит в пределах [1,N].

Пусть известны вероятности q_i того, что в случае неудачного поиска аргумент принимает значения A< K₁ при i=1, K_i-1<A< K_i при i=2,3,…,N и A> K_N при i=N+1. Тогда среднее число сравнений при неудачном поиске составляет…

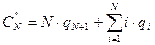
Для равновероятного случая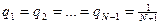

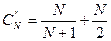
Среднее число сравнений при поиске в упорядоченном файле с учетом как удачного, так и неудачного поиска составляет

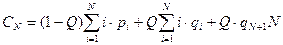
Для равновероятного случая эта формула принимает вид

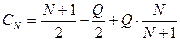
Поскольку упорядочивание файла по ключам не влияет на сложность удачного поиска, то, если заранее известно, что поиск в большинстве случаев удачный, файл можно упорядочить по убыванию вероятностей p_i. При этом удается уменьшить среднее число сравнений: ведь чем ближе часто запрашиваемая запись к началу файла, тем меньше сравнений требуется совершить при ее поиске.

Блочный поиск

Пусть файл или таблица упорядочены по возрастанию ключей и пусть на каждом шаге поиска имеется возможность выбирать любую по счету запись для сравнения ее ключа с аргументом поиска. Как организовать последовательность сравнений в этом случае, чтобы уменьшить сложность поиска?

Можно просматривать не каждую, а, например, сотые записи таблицы. Как только будет обнаружена запись с ключом, превышающим аргумент поиска, просматриваются (методом последовательного поиска) последние пропущенные 99 записей. Этот алгоритм называется поиском с пропусками или блочным поиском: записи группируются в блоки и сначала ищется нужный блок, а затем в нем ищется нужная запись.

Оптимальное число записей в блоке при равновероятных запросах равно квадратному корню из числа записей в файле. Среднее число записей, которые должны быть просмотрены при удачном поиске, в этом случае также равно 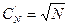. Примем это без доказательства.

Двоичный поиск

Пусть, как и в предыдущем случае, таблица поиска упорядочена по возрастанию ключей. Если теперь выбрать для проверки запись из середины таблицы, то, если эта запись не окажется искомой, множество возможных претендентов сократится приблизительно в два раза: искомая запись находится в одной из половин таблицы. На этой идее последовательного деления множества записей пополам основан двоичный или дихотомический поиск.

На каждом i-м шаге двоичного поиска считывается и сравнивается с аргументом запись 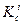, находящаяся примерно в середине некоторого множества 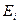последовательно расположенных записей таблицы

,

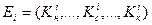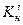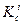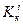где , и соответствуют начальной, серединной и конечной записям множества 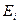на i-м шаге поиска. Взяв в качестве исходного множества 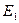всю таблицу 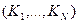, шаги повторяются до тех пор, пока либо аргумент поиска не совпадет с ключом сравниваемой записи 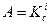, либо множество 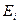не станет пустым. В первом случае поиск оканчивается удачно, во втором - неудачно. В качестве множества 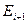для следующего шага берется правое или левое подмножество 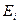текущего шага, причем

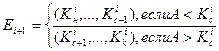
Рис. 2.4 поясняет алгоритм двоичного поиска на примере таблицы из 16 записей и значения аргумента 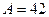. В этом методе особенно удивительно то, что уже после двух сравнений три четверти таблицы будут вне области поиска.

Рис.2.4.

Пример двоичного поиска записи в таблице

Двоичный поиск удобно представить в виде двоичного дерева (см. рис.2.5). Вершинами дерева двоичного поиска являются ключи, сравниваемые с аргументом поиска. При этом корнем является ключ записи, сравниваемой на первом шаге. Поиск можно интерпретировать как прохождение дерева от корня до искомой записи. Если достигнута конечная вершина, а заданный ключ не найден, то искомая запись в файле отсутствует. Число вершин на единственном пути от корня к искомой записи равно числу сравнений, выполняемых алгоритмом двоичного поиска при попытке отыскания нужной записи.

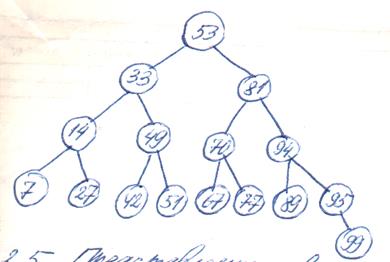
Рис.2.5.

Представление двоичного поиска в виде бинарного дерева

Среднее число сравнений в случае равновероятных запросов равно

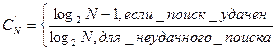
Ни один метод, основанный на сравнении ключей, не может дать лучших результатов при равновероятных запросах.

Рассмотрим случай неравновероятных запросов. Пусть, например, некоторая запись файла запрашивается с вероятностью, намного превосходящей суммарную вероятность запросов остальных записей. В этом случае, очевидно, что, прежде всего, целесообразно проверить эту запись, а только затем - остальные. Приведенные рассуждения показывают, что в случае неравновероятных запросов двоичный поиск, вообще говоря, не является оптимальным.

Даже в случае равновероятных запросов преимущества двоичного поиска не всегда бесспорны. Это, прежде всего, относится к ситуациям, когда время считывания записей непостоянно. В последнем случае доступ к серединным записям может быть сопряжен с большими затратами времени, чем доступ к записям в начале таблицы и алгоритм двоичного поиска оказывается менее эффективным.