Метод искусственного базиса

Часто, после приведения ОЗЛП к каноническому виду расширенная матрица системы линейных уравнений (СЛУ) не является К-матрицей (нет начального опорного плана), и, следовательно, решать такую КЗЛП симплекс-методом нельзя. Суть метода искусственного базиса состоит в следующем: строится такая вспомогательная КЗЛП (ВКЗЛП) с заранее известным опорным планом, по решению которой либо определяется начальный опорный план исходной задачи, либо устанавливается, что ее множество планов пусто.

Дано:

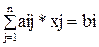, i = 1, ..., m, rang (A) = m < n, bi 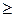0, i = 1, ..., m.

Найти: К-матрицу (начальный опорный план).

Построим следующую ВКЗЛП:

,

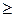, i = 1, ..., m, xj 0, j = 1, ..., n, yi 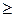0, i = 1, ..., m, yi – искусственные переменные.

Очевидно, начальный опорный план ВКЗЛП имеет вид:

,

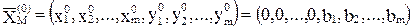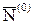= (n+1, n+2, ..., n+m).

Применяя симплекс-метод, находят

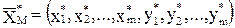– решение ВКЗЛП.

Замечание: ВКЗЛП всегда разрешима, так как множество ее планов не пусто, а целевая функция ограничена.

Теорема: Если , то 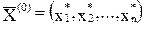– начальный опорный план исходной КЗЛП. Если 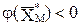, то множество планов исходной КЗЛП пусто и, следовательно, она неразрешима.

Пример: F(X) = 5×x1 + 3×x2 + 4×x3 - x4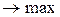

x1 + 3×x2 + 2×x3 + 2×x4 = 3

2×x1 + 2×x2 + x3 + x4 = 3

.

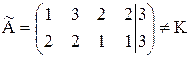x1 + 3×x2 + 2×x3 + 2×x4 + y1 = 3

x1 + 3×x2 + 2×x3 + 2×x4 + y2 = 3

x_j 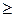0, j = 1, ..., 4, y₁,₂ 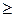0.

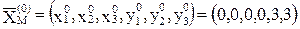
= (5,6), 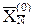= (3,3), 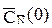= (-1,-1).

Таблица 1

								=
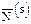
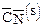
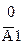
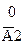
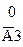
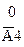
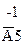
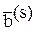
	-1 -1
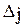
		-3	-5	-3	-3			F(x)=-6
	-1	1/3 4/3		2/3 -1/3	2/3 -1/3
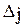
		-4/3		1/3	1/3			-1
				3/4 -1/4	3/4 -1/4			3/4 3/4
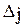
								F(x)=0

Замечание:

По мере выхода искусственных переменных из базиса, вычисления в соответствующих клетках симплекс-таблицы не проводятся.

Получили оптимальный опорный план ВКЗЛП.

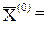(3/4,3/4,0,0,0,0), , (3/4,3/4,0,0).

Теперь решаем симплекс-методом исходную задачу:

F(X)= 5×x1 + 3×x2 + 4×x3 - x4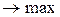

x2 + 3/4×x3 + 3/4×x4 = 3/4

x1 - 1/4×x3 - 1/4×x4 = 3/4

x_j 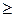0, j = 1, ..., 4.

Таблица 2

						=
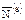
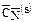
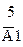
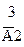
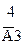
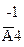
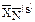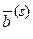
				3/4 -1/4	3/4 -1/4	3/4 3/4
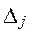
				-3		F(x) = 6
			4/3 1/3
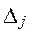
						F(x) = 9

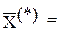(1, 0, 1, 0), 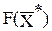= 9.