Альтернативные оптимальные решения

Когда гиперплоскость, представляющая целевую функцию, параллельна гиперплоскости, соответствующей связывающему ограничению ( которое в точке оптимума выполняется как точное равенство), целевая функция принимает одно и то же оптимальное значение в некоторой совокупности точек пространства решений. Такие решения называются альтернативными оптимальными решениями.

Приводимый ниже пример рассматриваемой ситуации показывает, что при этом обычно существует бесконечное множество альтернативных решений.

Пример:

F( 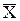)= 2×x1 + 4×x2 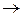max

при ограничениях

x1 + 2×x2 £ 5 (ресурс 1)

x1 + x2 £ 4 (ресурс 2)

x1 ³ 0, x2 ³ 0.

Рис.2 иллюстрирует условия данной задачи ЛП, особенность которой состоит в том, что прямая, представляющая целевую функцию, параллельна прямой, соответствующей одному из связывающих ограничений.

Рис. 2. Геометрическая интерпретация альтернативных базисных решений

Это обусловливает наличие альтернативных оптимальных решений. Любая точка отрезка ВС представляет собой альтернативный оптимум, причем в каждой из этих точек целевая функция имеет одно и то же оптимальное значение. Приведем решение задачи в симплекс-таблице.

Таблица 2

						=
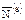
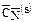
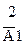
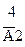
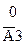
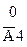
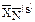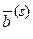
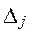
		-2	-4			F(x) = 0
		1/2 1/2		1/2 -1/2		5/2 3/2
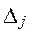
						F(x) = 10
				-1	-1
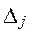
						F(x) = 10

Каким образом по результатам итерации можно узнать о наличии альтернативных решений?

Нулевое значение симплексной разности у небазисной переменной свидетельствует о том, что ее включение в базис не изменит значения целевой функции, но приведет к изменению других переменных.

Любое решение, соответствующее точке ( 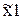, 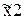) принадлежащей отрезку ВС, можно определить как положительно-взвешенное среднее двух полученных оптимальных базисных решений, соответствующих точкам В и С. Поэтому, используя координаты точек В и С

В: х1 = 0; х2 = 5/2;

С: х1 = 3; х2 = 1;

и полагая 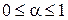, можно выразить координаты любой точки отрезка ВС следующим образом:

,

.

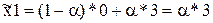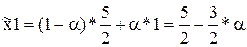Информация о наличии альтернативных оптимумов дает возможность выбора альтернативного варианта в наибольшей степени отвечающего сложившейся производственной ситуации.