Распределения случайных величин
Уравнение кривой нормального распределения (закон Гаусса) имеет вид
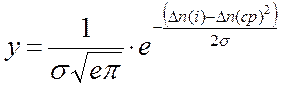 , (7)
, (7)
где σ – среднее квадратическое отклонение, определяемое по формуле
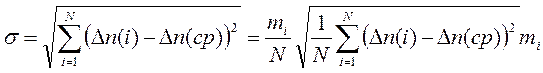 , (8)
, (8)
где ∆П (i)_ – текущее значение погрешности позиционирования;
∆П (ср) – среднее взвешенное арифметическое значение этой погрешности, которое, в свою очередь, можно определить по формуле
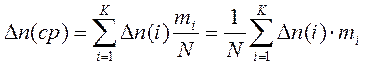 (9)
(9)
где mi – частота попадания значений ∆П в каждый интервал, на которые разбиты оси эллипса рассеяния;
N – количество рабочих циклов позиционирования, когда производилось определение погрешности позиционирования;
mi/N – частость достижения случайной величиной значений, попадающих в данный интервал;
k – количество интервалов (следует выбрать k = 7…8).
Пример расчета ∆П (ср) (рис. 8):
∆П (ср) = 1/100 (0,01 x 5 + 0,03 x 8 + 0,05 x 19 + 0,07 x 28 + 0,09 x 22 + 0,11 х x 13 + + 0,13 x 5) = 1/100 (0,05+0,24+0,95+1,96+1,98+1,43+0,65) = 1/100 х 7,26 = = 0,0726 ≈ 0,073 мм .
Как известно, координата центра группирования совпадает со значением среднего взвешенного арифметического случайной величины, в данном случае – погрешности ∆П, и является математическим ожиданием величины этой погрешности.
Если теоретическая кривая нормального распределения имеет симметричный вид (рис. 9 а), то практически под влиянием различных причин систематического и случайного характера вершина кривой распределения может быть смещена относительно середины эллипса рассеяния.
Одной из причин может служить влияние жестких упоров, по которым осуществляется позиционирование руки робота (рис. 9 б). Кривая может носить также усеченный вид.
Для построения теоретической кривой нормального распределения рассчитывают координаты опорных точек:
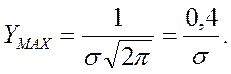 (10)
(10)

Рис. 8. Пример построения гистограммы и полигона практического
распределения погрешности позиционирования (N =100 циклов)
Ординаты точек перегиба с абсциссами, равными σ:
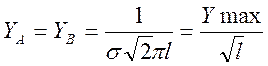 . (11)
. (11)
Или приближенно: Y A = Y B ≈ 0,6 YMAX ≈ 0,24/ σ. (12)
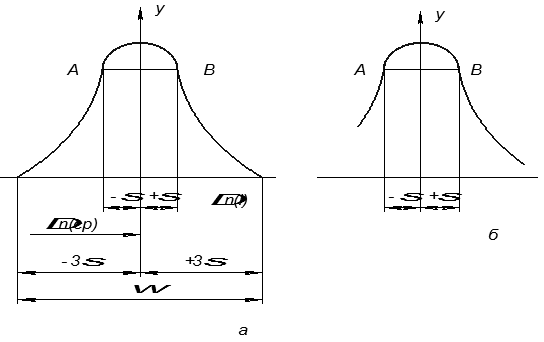
Рис. 9. Теоретическая кривая: а – нормального закона распределения;
б – усеченного нормального закона
Этих значений достаточно для построения теоретической кривой нормального распределения, которую необходимо совместить с уже построенным полигоном практического распределения ∆П. Следует учесть, что ветви кривой асимптотически приближаются к оси абсцисс на расстоянии
3σ от положения ее вершины. При этом 99,73% значений исследуемой погрешности попадает в этот интервал, равный 6σ.
Следует провести проверку сходимости практического и теоретического распределений погрешности позиционирования. Для этого используют, например, критерий согласия Пирсона (Х-квадрат). Все поле изменения погрешности ∆ n разбивают на К интервалов (рекомендуемое К = 7 – 8).
Определяют опытное значение критерия X2 :
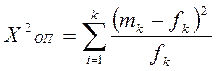 , (13)
, (13)
где К – количество интервалов или сравниваемых частот;
mК – практическое значение частоты, т.е. количества значений ∆П в данном интервале ( оно определяется с использованием гистограммы);
f – теоретическая частота, определяемая как количество значений ∆П , снятое с кривой нормального распределения.
Затем вычисляют число степеней свободы по формуле
n = k – p – 1, (14)
где р – число параметров распределения (р = 2). По таблице находят критическое значение x2кр. Если соблюдается соотношение Х2оп < x2кр, то практическое распределение ∆П соответствует нормальному закону с определенной степенью вероятности. Необходимым условием применения критерия X2 является наличие 5 – 10 значений погрешности в каждом интервале.
Табл. 3. Значения критерия Пирсона
| Число степеней свободы, n | Вероятность | |||
| 0,99 | 0,95 | 0,80 | 0,50 | |
| 0,020 0,115 0,300 0,550 0,870 1,240 | 0,103 0,352 0,710 1,140 1,630 2,170 | 0,446 1,005 1,650 2,340 3,070 3,320 | 1,386 2,366 3,360 4,350 5,350 6,340 |
Далее надо сделать обобщения о величине погрешности позиционирования c учетом ее характеристик как случайной величины, а также сопоставить полученные значения с паспортными данными промышленного робота.
Для этого в том же масштабе на гистограмму нанести (рис. 8) значение погрешности позиционирования робота данной модели (табл. 1). Устанавливают процент показаний, выходящих за указанные границы, и делают заключение о реальной точности робота.
Далее следует сделать выводы о влиянии погрешности ∆П (∆ПП) на безотказность выполнения технологических операций, требующих различной точности робота, и уточнить порядок выбора нужной модели промышленного робота.
Дата добавления: 2017-10-09; просмотров: 568;
