Расчет координатных составляющих погрешности

Для этого можно, в зависимости от заданного метода, использовать

следующие соотношения.

Метод I (рис. 2).

По оси ОХ: ∆Х_В (1) = А_ХВ (1) – А_ХВ (min); (1)

∆Х_В (2) = А_ХВ (2) – А_ХВ (min);

∆Х_В (3) = А_ХВ (3) – А_ХВ (min);

…

∆Х_В (i) = А_ХВ (i) – А_ХВ (min);

по оси OY: ∆Y_В (1) = А _YВ(1) – А_YВ (min); (2)

∆Y_В (2) = А _YВ(2) – А_YВ (min);

∆Y_В (3) = А _YВ(3) – А_YВ (min);

…

∆Y_В (i) = А _YВ(i) – А_YВ (min),

где А_ХВ (min) и А_ХВ (min) – наименьшие значения координат всех
i точек, измеренных вдоль осей ОX и ОY соответственно, иначе говоря, это те показания индикаторов, которые установлены в верхнем уровне.

Удобно перед началом измерений установить все индикаторы верхнего и нижнего уровней на «нуль», тогда их показания можно принять за приращения по соответствующим координатам OX и OY.

Метод II (рис. 3).

По оси ОХ: ± ∆Х_В (1) = А_ХВ (1) – А_ХВ (0); (3)

± ∆Х_В (2) = А_ХВ (2) – А_ХВ (0);

± ∆Х_В (3) = А_ХВ (3) – А_ХВ (0);

…

± ∆Х_В (i) = А_ХВ (i) – А_ХВ (0);

по оси OY: ± ∆Y_В (1) = А_YВ (1) – А_YВ (0); (4)

± ∆Y_В (2) = А_YВ (2) – А_YВ (0);

± ∆Y_В (3) = А_YВ (3) – А_YВ (0);

…

± ∆Y_В (i) = А_YВ (i) – А_YВ (0),

где А_ХВ (0) и А_YВ (0) – координаты "нулевой" точки позиционирования, т.е. точки, соответствующей настройке датчиков на "нуль" по контрольной оправке до начала рабочих циклов ПР.

2.5. Графическая иллюстрация топографии распределения случайных величин координатных составляющих (∆Х_В и ∆Y_В )

Это построение лучше сделать в увеличенном масштабе. Надо нанести полученные значения на лист бумаги, используя лишь данные по измерениям погрешности в верхнем уровне. Очертить эллипс рассеяния по крайним точкам и нанести оси координат ОХ и OY для отсчета ∆_П в соответствии с заданным методом расчета (см. методы I и II, изложенные выше).

2.6. Определение фактических значений погрешности ∆_П

Определяя значения погрешности позиционирования ∆_П (или ∆_ПП), ее считают геометрической суммой указанных составляющих погрешностей:

∆_П = 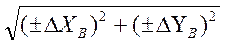, (5)

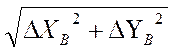∆_ПП = . (6)

Используя полученные данные, построить гистограммы и полигоны практического распределения случайных величин-составляющих ∆ХВ и ∆YВ, а также искомой погрешности ∆П. На полигон распределения погрешности ∆П надо нанести ее паспортные значения изучаемой погрешности для данной модели промышленного робота, произвести ее сравнение с полученными данными.