Макет таблицы, представляющий результат дискретной группировки
| Номер группы i | Значения группировочного признака, xi | Число единиц совокупности в группе, fi | Доля единиц в _рупппе = fi/N |
| Х1 | |||
| Х2 | |||
| … | |||
| К | Хк | ||
| Итого: | - | N |
Пример. Группа из 15 человек представляет собой статистическую совокупность. Каждый студент характеризуется признаком х – оценкой по дисциплине «Статистика» (пятибалльная система). Построить дискретную группировку по признаку х.
| Номер студента | |||||||||||||||
| Оценка |
Число вариантов значений признака равно 4 – 2,3,4,5.
| Номер группы i | Оценка по статистике | Число студентов | Доля студентов |
| 0,067 | |||
| 0,33 | |||
| 0,47 | |||
| 0,133 | |||
| Итого: | - | 1,0 |
Интервальные группировки рекомендуются, если группировочный признак имеет большое число вариантов значений.
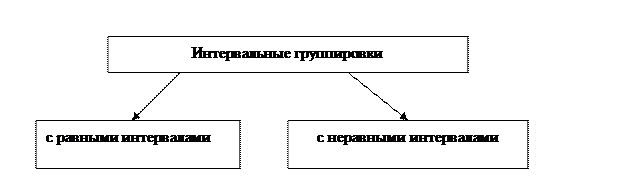
Алгоритм построения группировки с равными интервалами:
1) Определяется количество групп. Для совокупностей объемом свыше 30 единиц используют формулу Стерджесса:
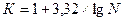
2) Определяется длина интервала:
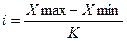
3) Определяются границы каждого интервала
4) Результаты заносят в таблицу.
Пример. Группа из 15 человек представляет собой статистическую совокупность. Каждый студент характеризуется признаком х – суммой баллов, набранной при изучении дисциплины «Статистика» в соответствии с балльно-рейтинговой системой (максим. сумма 100). Построить равноинтервальную группировку по признаку х.
| Номер студента | |||||||||||||||
| Баллы |
Возьмем число групп 3. Величина интервала =23
| Номер группы I | Баллы по статистике | Число студентов | Доля студентов |
| 30-53 | 0,267 | ||
| 53-76 | 0,267 | ||
| 76-99 | 0,467 | ||
| Итого: | 1,0 |
Алгоритм построения аналитической группировки:
1) Выделяют признак-фактор х и признак-результат у.
2) Производится группировка единиц совокупности по х.
3) По каждой полученной группе отбираются соответствующие значения признака у, и на их основе рассчитывается обобщающий показатель (чаще всего среднее значение)
4) Анализируются результаты группировки и делается вывод о наличии или отсутствии взаимосвязи.
5. Ряды распределения
Упорядоченное расположение единиц совокупности по изучаемому признаку представляет собой ряд распределения.
Любой ряд распределения позволяет получить информацию:
- о возможных вариантах значения признака, которые встречаются в данной статистической совокупности
- как часто встречаются отдельные значения данного признака.
В зависимости от признака различают:
-вариационные ряды распределения
-атрибутивные ряды распределения.
Элементы ряда распределения:
§ Значение признака (варианта) -хi
§ Частота fi – число единиц совокупности с данным значением признака.
Сумма всех частот определяет численность всей совокупности.
§ Частостью называются частоты, выраженные в долях единицы или в %.
§ Накопленная частота – частота нарастающим итогом.
§ Накопленная частость – частость нарастающим итогом.
Если варианты расположены по возрастанию или убыванию, то ряды называются ранжированными.
В зависимости от характера вариации признака различают:
- дискретные вариационные ряды распределения
- интервальные ряды распределения.
Ряды распределения удобнее всего анализировать при помощи их графического изображения. Наглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма.
Полигон используется при изображении дискретных вариационных рядов. По оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака, а по оси ординат – величины частот. Точки, полученные на пересечении абсцисс и ординат, соединяются прямыми линиями, в результате получают ломаную линию, называемую полигоном частот.
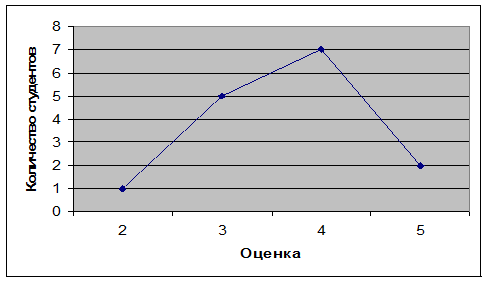
Рис.3. Полигон распределения студентов по полученной оценке.
Для изображения интервального вариационного ряда применяется гистограмма. По оси абсцисс – длина интервала, по оси ординат – частоты. Гистограмма может быть преобразована в полигон распределения, если соединить прямыми линиями середины сторон прямоугольников.
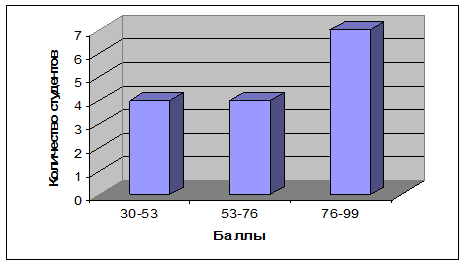
Рис. 4. Гистограмма распределения студентов по заработанным баллам
При построении гистограммы распределения ряда с неравными интервалами по оси ординат наносят плотность распределения признака в соответствующих интервалах.
Для графического изображения вариационных рядов может использоваться кумулята – ряд накопленных частот. При построении кумуляты интервального ряда распределения по оси абсцисс откладываются варианты ряда, по оси ординат – накопленные частоты, которые наносят на поле графиков перпендикуляров к оси абсцисс в верхних границах интервалов. Затем перпендикуляры соединяют ломаной.
Дата добавления: 2017-09-19; просмотров: 827;
