Тема. Средние величины. Структурные средние
Вопросы:
1. Средняя арифметическая величина. Основные свойства средней арифметической.
2. Средняя геометрическая, средняя гармоническая, средняя квадратическая.
3.Структурные средние: мода, медиана.
4. Квартили и децили распределения.
1. Средняя арифметическая величина. Основные свойства средней арифметической
Средняя величина - обобщающая характеристика однотипных явлений по одному из варьирующих признаков.
Определить среднюю можно через исходное соотношение средней или ее логическую формулу:
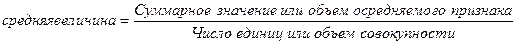 .
.
Для изучения и анализа социально-экономических явлений применяются различные средние величины: средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая, кубическая, а также структурные средние – мода, медиана, квартили, децили.
Средние могут рассчитываться в двух вариантах: взвешенные и невзвешенные.
При расчете взвешенных средних величин веса, могут быть представлены как абсолютными величинами, так и относительными (в % или долях единицы).
Средней арифметической величиной называется такое значение признака в расчете на единицу совокупности, при вычислении которого общий объем признака в совокупности сохраняется неизменным.
Исходя из определения, формула средней арифметической величины имеет вид:
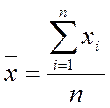 . (1)
. (1)
По данной формуле вычисляются средние величины первичных (объемных) признаков, если известны индивидуальные значения признака. Если изучаемая совокупность велика, исходная информация чаще представляет собой ряд распределения, или группировку, то расчет проводят по средней арифметической взвешенной
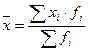 . (2)
. (2)
В качестве весов здесь выступают численность единиц совокупности в группе.
Пример. Имеются данные о средней заработной плате сотрудников двух предприятий за январь.
Таблица 1
| № предприятия | Январь | |
| Средняя заработная плата, руб. | Численность работников, человек | |
Вычислить среднюю заработную плату сотрудников по двум предприятиям.
Решение.
Определим исходные соотношения средней (ИСС) для показателя «средняя заработная плата».
ИСС = 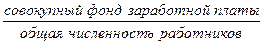 .
.
Фонд заработной платы можно получить умножением средней заработной платы на численность работников. Поэтому общая средняя может быть рассчитана по формуле средней арифметической взвешенной:
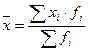 =
= 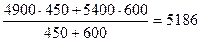 руб.,
руб.,
где xi - i –тый вариант осредняемого признака;
fi - вес i –ого варианта.
Если при группировке значения осредняемого признака заданы интервалами, то при расчете средней арифметической величины в качестве значения признака в группах принимают середины этих интервалов, т.е. исходят из гипотезы о равномерном распределении единиц совокупности по интервалу значений признака. Для открытых интервалов в первой и последней группе, если таковые есть, значения признака надо определить экспертным путем исходя из сущности, свойств знака и совокупности.
Таблица. 5.2
| Группы рабочих по возрасту, лет | Число рабочих, 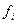
| Середина интервала,
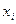
| 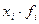
|
| А | |||
| До 20 20—30 30-40 40-50 Старше 50 | 18,5 57,5 | ||
| Итого | 34,56 |
Можно минимальный возраст рабочих считать 17 лет. В таком случае первый интервал будет от 17 до 20 лет, а максимальный возраст — 65 лет, тогда последний интервал — 50—65 лет.
Средний возраст рабочих, рассчитанный по формуле (2) с заменой точных значений признака в группах серединами интервалов, составил: 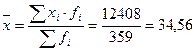 лет.
лет.
Расчет средних вторичных (относительных) признаков. Сумма таких показателей сама по себе реальной величиной какого-либо признака в совокупности не является.
Пример. Рассчитать среднюю долю потребительских товаров в общем выпуске промышленной продукции по совокупности предприятий (табл. 5.3). В этом случае весом должен являться общий объем всей продукции предприятия.
Таблица 3
Объем и структура промышленной продукции
| Номер предприятия | Объем всей продукции, млн руб. 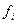
| Доля товаров, %, 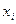
| Объем выпуска товаров млн. руб., 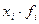
|
| 103,5 247,0 124,8 140,2 | |||
| Итого | 615,5 |
Тогда средняя доля товаров в продукции четырех предприятий равна:
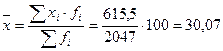
Дата добавления: 2017-09-19; просмотров: 528;
