Тема. Выборочное наблюдение

Вопросы:

1. Выборочное наблюдение, его задачи
2. Виды выборочного наблюдения
3. Ошибки выборочной совокупности

4. Задачи, решаемые при применении выборочного наблюдения

1. Выборочное наблюдение, его задачи

Статистическое наблюдение можно организовать сплошное и несплошное. Сплошное наблюдение предусматривает обследование всех единиц совокупности и связано с большими трудовыми и материальными затратами. Изучение не всех единиц совокупности, а лишь некоторой ее части, по которой следует судить о свойствах всей совокупности в целом, можно осуществить несплошным наблюдением. Самым распространенным является выборочное наблюдение.

Выборочное наблюдение – это такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, отобранная часть изучается, а результаты распространяются на всю исходную совокупность.

Совокупность, из которой производится отбор, называется генеральной. Совокупность отобранных единиц называют выборочной совокупностью. Числовые характеристики генеральнойсовокупности (средняя, дисперсия и др.) называют параметрами генеральной совокупности. Числовые характеристики, полученные на основе выборки, называются оценками параметров.

При применении выборочного метода используют две основные характеристики:

- среднюю величину количественного признака

- относительную величину альтернативного признака, характеризующая долю единиц в статистической совокупности, которые отличаются от единиц этой совокупности только наличием изучаемого признака. (например, доля нестандартных изделий во всей партии товара)

Таблица 1

Точечные оценки статистических характеристик

Оценка	Формула расчета
Средний размер признака
Доля
Дисперсия

Выборочное наблюдение должно быть организовано и проведено в строгом соответствии с научными принципами теории выборочного метода. Такими принципами являются:

- обеспечение случайности отбора единиц;

- достаточное число отобранных единиц.

Соблюдение этих принципов позволяет получить объективную гарантию репрезентативности полученной выборочной совокупности.

Основная задача выборочного наблюдения – на основе характеристик выборочной совокупности получить достоверные суждения о генеральной совокупности.

Выборочный метод наблюдения согласно рекомендациям Методологических положений по статистике включает следующие этапы:

- определение генеральной совокупности и единиц наблюдения, обладающих первичной информацией, необходимой для решения задач обследования;

- создание основы выборки (списка элементов совокупности);

- формирование выборочной совокупности путем отбора элементов основы;

- распространение данных по выборке на генеральную совокупность.

Последний этап зависит от примененного способа отбора элементов в выборку и формулы оценивания характеристик генеральной совокупности по данным выборки.

Широкое применение выборочного метода в статистической практике вызвано рядом преимуществ по сравнению со сплошным наблюдением.

1. Быстрота получения результатов.

2. Значительное снижение стоимости наблюдения.

3. Возможность лучшей организации проведения обследования.

4. Возможность расширения программы наблюдения

5. Возможность использования в тех случаях, когда проведение сплошного наблюдения методологически невозможно.

2. Виды выборочного наблюдения

Выборочная совокупность должна наиболее полно и адекватно отображать свойства генеральной совокупности, чтобы было возможно получить достоверные выводы о свойствах последней. Репрезентативность выборки обеспечивается только при объективности отбора данных. Отбором называется процесс формирования выборочной совокупности из элементов генеральной. По способу организации различают следующие основные виды выборки:

1. Собственно-случайная (простая). Самый наиболее распространенный способ отбора. Его суть состоит в том, что включение в выборку того или иного элемента является случайным. Различают:

• Повторный отбор – единица, попавшая в выборку возвращается снова в генеральную совокупность. Данная выборка в социально-экономической жизни встречается редко.

• Бесповторный отбор– позволяет получить более точные оценки при прочих равных условиях, чем повторный.

2. Механическая – это бесповторный отбор элементов через равные интервалы. Например, отбор каждой 20 детали для проверки качества. Механический отбор обычно применяют для постепенно формирующейся выборки с заранее неизвестным объемом.

3. Серийная – предполагает случайный отбор из генеральной совокупности не отдельных единиц, а их равновеликих групп (гнезд, серий), с тем, чтобы в таких группах подвергать наблюдению все без исключения единицы совокупности. Применяют, когда исследуемый признак колеблется внутри серий незначительно.

4. Расслоенная – используется для отбора единиц из неоднородной совокупности. Генеральную совокупность разбивают на несколько качественно однородных групп, затем из каждой группы собственно случайным или механическим способом производится индивидуальный отбор единиц в выборочную совокупность. Если пропорции между группами в выборке совпадают с пропорциями между группами в генеральной совокупности, то имеет типический отбор.

5. Многоступенчатая – отбор, при котором из генеральной совокупности сначала (на 1-ступени) извлекаются укрупненные единицы (группы), затем более мелкие и т.д. до тех пор, пока на последней ступени не будут отобраны единицы, которые подвергаются наблюдению.

6. Многофазная – отбор, при котором единица отбора сохраняется на каждом этапе (фазе) отбора.

По числу единиц в выборочной совокупности выборки делят на:

а) большие (n>30)

б) малые (n<30).

3. Ошибки выборочной совокупности

Статистическая оценка, полученная по данным выборки, отличается от генеральной характеристики на величину ошибки наблюдения (регистрации) и величину ошибки репрезентативности (выборки). Понятие репрезентативности (представительства) отобранной совокупности следует понимать как ее представительство по наиболее существенным признакам, т.е. признакам, которые оказывают наиболее значимое влияние на изучаемые характеристики.

Ошибкой репрезентативности называют расхождение между значениями показателей, полученных по выборке, и соответствующими параметрами генеральной совокупности. Различают случайные и систематические ошибки выборки (рис.1).

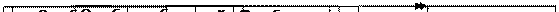
Рис.1. Ошибки выборочной совокупности

Систематические ошибки могут быть связаны с нарушением правил отбора или условий реализации выборки.

Случайные ошибки репрезентативности называются ошибкой выборки – отклонения, возникающие от недостаточно равномерного представления в выборочной совокупности различных единиц генеральной совокупности.

Различают:

1. Среднюю ошибку выборки – характеризует меру отклонений выборочных показателей от аналогичных показателей генеральной совокупности. Формулы расчета средней ошибку выборки зависят от способа формирования выборочной совокупности. Для простой случайной выборки формулы представлены на рис.2.

2. Предельную ошибку выборки – это максимально возможная при данной вероятности ошибка выборки. Определяется предельная ошибка выборки по формуле:

, (1)

где - средняя ошибка выборки;

- коэффициент доверия, определяемый по таблице в зависимости от уровня надежности (вероятности).

Коэффициент доверия t 1,0 2,0 3,0

Вероятность Ф(t) 0,683 0,954 0,997

Простая случайная

Выборка

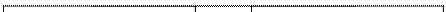
Средняя ошибка Средняя ошибка

для средней для средней

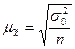
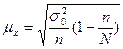
для доли для доли

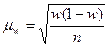
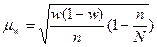
Рис.2. Формулы расчета средней ошибки для простой случайной выборки

s₀² - дисперсия признака х в выборочной совокупности

w - доля единиц, обладающих исследуемым признаком

n - объем выборочной совокупности

N - объем генеральной совокупности

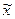- выборочная средняя

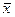-генеральная средняя.

4. Задачи, решаемые при применении выборочного метода

При применении выборочного метода возникают три основные задачи:

1. Определение объема выборки, необходимого для получения требуемой точности результатов с заданной вероятностью.

При проектировании выборочного наблюдения возникает вопрос о необходимой численности выборки. Эта численность может быть определена на основе допустимой ошибки при выборочном наблюдении исходя из вероятности и на основе способа отбора. Для определения объема случайной выборки используют следующие формулы:

при повторном отборе (2)

при бесповторном (3)

2. Определение пределов генеральных характеристик гарантированных с заданной вероятностью по результатам выборки.