Тема. Статистическое изучение динамики социально-экономических процессов
Вопросы:
1. Описательные характеристики динамики.
2. Выявление основной тенденции развития и формирование моделей для анализа и прогнозирования.
3. Прогнозирование на основе анализа временных рядов.
1. Описательные характеристики динамики
Статистическое изучение динамики показателей таможенной статистики основывается на обработке рядов динамики, включая анализ изменения их уровней ряда, выявление основной тенденции и закономерностей развития.
Временной ряд представляет собой последовательность измерений в последовательные периоды времени. Анализ временных рядов основывается на предположении, что последовательные значения в наборе данных наблюдаются через равные промежутки времени.
В зависимости от способа выражений уровней (в виде абсолютных, относительных и средних величин) ряды динамики подразделяются на ряды абсолютных, относительных и средних величин.
В зависимости от того, выражают уровни ряда состояние явлений на определенные моменты времени (на начало месяца, года) или его величину за определенные интервалы времени (за месяц, квартал) различают соответственно моментные и интервальные ряды.
Примером моментного временного ряда является ряд динамики, показывающий число принятых грузовых таможенных деклараций на 1 июня каждого года за несколько лет.
Примером интервального ряда динамики может быть ряд, содержащий ежемесячные (ежедневные, ежеквартальные, ежегодные) данные об экспорте (импорте) Российской Федерации.
Изучение социально-экономических процессов на основе анализа временных рядов включает следующие этапы:
1) постановка задачи и подбор исходной информации;
2) предварительный анализ исходных временных рядов и формирование модели (моделей) анализа и прогнозирования;
3) оценка параметров и качества модели (моделей);
4) построение прогноза, комментарий полученного прогноза.
На первом этапе формулируется цель исследования, осуществляется содержательный (логический и экономический) анализ исследуемого процесса; задается период упреждения прогноза (на сколько шагов вперед делается прогноз).
На этапе предварительного анализа временных рядов проверяется их соответствие требованиям объективности, сопоставимости, полноты, однородности и устойчивости; строится график динамики и рассчитываются основные динамические характеристики (приросты, темпы роста, темпы прироста). Исходя из целей исследования и качества имеющейся информации выбираются модели для описания развития.
При оценке параметров моделей могут использоваться различные процедуры, в зависимости от типа модели, но всегда следует стремиться к максимальному приближению модели к исходным данным. Этот же принцип используется при исследовании качества моделей и выборе лучшей из них: чем ближе модель к исходным данным, тем лучше она описывает процесс с формальной точки зрения.
Далее прогноз должен быть подвергнут критическому рассмотрению с целью выявления возможных противоречий известным фактам и сложившимся к настоящему моменту представлениям о характере развития в периоде упреждения прогноза.
На основании имеющихся абсолютных значений основных показателей рассчитываются характеристики динамических рядов. Характеристики динамических рядов – это показатели, которые характеризуют изменения явления во времени.
К статистическим характеристикам динамического ряда относятся:
1. Приросты (базисные, цепные, средний).
2. Темпы роста (базисные, цепные, средний).
3. Темпы прироста (базисные, цепные, средний).
Абсолютный прирост (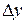 ) – это разность между последующим и предыдущим уровнями ряда (цепные) или начальным уровнем ряда (базисные). Цепной абсолютный прирост характеризует последовательное изменение уровней ряда, а базисный абсолютный прирост – изменение нарастающим итогом. Абсолютный прирост показывает, на сколько абсолютных единиц изменился данный уровень по сравнению с предыдущим уровнем при цепном способе и с начальным уровнем при базисном способе.
) – это разность между последующим и предыдущим уровнями ряда (цепные) или начальным уровнем ряда (базисные). Цепной абсолютный прирост характеризует последовательное изменение уровней ряда, а базисный абсолютный прирост – изменение нарастающим итогом. Абсолютный прирост показывает, на сколько абсолютных единиц изменился данный уровень по сравнению с предыдущим уровнем при цепном способе и с начальным уровнем при базисном способе.
Для первого случая справедливо выражение
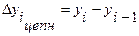 ,(1)
,(1)
где 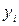 – i-ый уровень ряда;
– i-ый уровень ряда;
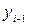 – i-1-ый уровень ряда.
– i-1-ый уровень ряда.
Для второго случая используется формула
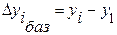 ,(2)
,(2)
где 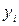 – i-ый уровень ряда;
– i-ый уровень ряда;
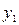 – начальный, базисный уровень ряда.
– начальный, базисный уровень ряда.
Между цепным и базисным абсолютным приростом существует взаимосвязь – сумма цепных дает соответствующий базисный абсолютный прирост.
За весь период, описываемый рядом, абсолютный прирост выразится как разность между последним и первым уровнем ряда

Абсолютный прирост может быть как положительным, так и отрицательным и обязательно имеет единицы измерения и размерность.
Коэффициент (темп) роста (Тр, Кр) – это соотношение последующего уровня ряда к предыдущему (цепной) или постоянному, принятому за базу сравнения (базисный):
1) цепные коэффициенты (темпы) роста рассчитываются по формуле:
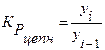
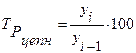 , (3)
, (3)
где 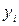 – i-ый уровень ряда;
– i-ый уровень ряда;
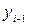 – i-1-ый уровень ряда.
– i-1-ый уровень ряда.
2) базисные коэффициенты (темпы) роста рассчитываются по формуле:
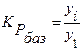
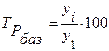 , (4)
, (4)
где 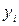 – i-ый уровень ряда;
– i-ый уровень ряда;
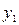 – начальный, базисный уровень ряда.
– начальный, базисный уровень ряда.
Цепной способ характеризует последовательное изменение, а базисный способ – изменение нарастающим итогом.
Между цепными и базисными коэффициентами роста существует взаимосвязь – произведение цепных коэффициентов роста дает соответствующий базисный коэффициент роста.
Темп прироста показывает, на сколько процентов изменяется данный уровень по сравнению с предыдущим уровнем ряда при цепном способе и с начальным уровнем ряда при базисном способе.
Для первого случая справедливо выражение
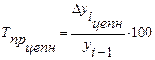 , (5)
, (5)
где 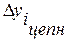 – цепной абсолютный прирост i-го уровня ряда;
– цепной абсолютный прирост i-го уровня ряда;
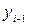 – i-1-ый уровень ряда.
– i-1-ый уровень ряда.
Во втором случае используется формула
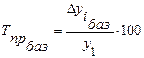 , (6)
, (6)
где 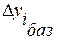 – базисный абсолютный прирост i-го уровня ряда;
– базисный абсолютный прирост i-го уровня ряда;
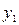 – начальный, базисный уровень ряда.
– начальный, базисный уровень ряда.
Темп прироста обычно выражается в процентах и показывает, на сколько процентов увеличился или уменьшился текущий уровень по сравнению с предыдущим (базисным).
Темп и коэффициент прироста также можно определить исходя из темпа и коэффициента роста:
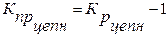 , (7)
, (7)
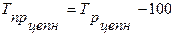 , (8)
, (8)
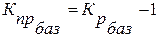 ,(9)
,(9)
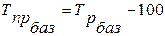 .(10)
.(10)
Так как показатели в течение рассматриваемого периода времени изменяются, изменяются и характеристики ряда. Поэтому, чтобы получить общее представление об изменении данных показателей, следует найти обобщающие характеристики, то есть средние величины.
Средний абсолютный прирост (  ) – это средняя из абсолютных приростов за равные промежутки времени:
) – это средняя из абсолютных приростов за равные промежутки времени:
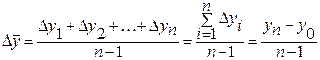 , (11)
, (11)
где 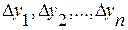 - соответствующий абсолютный прирост;
- соответствующий абсолютный прирост;
n-1 – количество изменений за данный период;
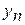 - последний уровень ряда;
- последний уровень ряда;
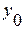 - начальный, базисный уровень ряда.
- начальный, базисный уровень ряда.
Средний темп роста ( 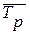 ) - это средняя из темпов роста за данный период, которая показывает, во сколько раз в среднем (за год, месяц) изменяется явление.
) - это средняя из темпов роста за данный период, которая показывает, во сколько раз в среднем (за год, месяц) изменяется явление.
Средний темп роста определяется всегда по средней геометрической. Средний темп роста можно определить исходя из цепных коэффициентов (темпов) роста:
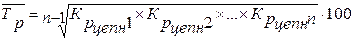 , (12)
, (12)
или абсолютных уровней ряда (базисного темпа роста):
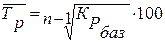 , (13)
, (13)
где 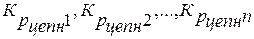 - соответствующие цепные кэффициенты роста (yi / yi-1);
- соответствующие цепные кэффициенты роста (yi / yi-1);
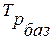 - базисный темп роста за весь период (yn / y0);
- базисный темп роста за весь период (yn / y0);
n-1 – количество изменений за данный период.
Средний темп роста обычно выражается в коэффициентах, но может быть и в процентах.
Средний темп прироста ( 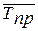 ) – характеризует темп прироста в среднем за период и определяется на основе среднего темпа роста:
) – характеризует темп прироста в среднем за период и определяется на основе среднего темпа роста:
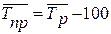 , (14)
, (14)
где 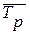 - средний темп роста.
- средний темп роста.
Средний темп прироста показывает, на сколько процентов изменился уровень ряда в среднем за данный период.
Средний темп прироста выражается в коэффициентах (коэффициент прироста) или в процентах.
Вычисление данных показателей является первым этапом анализа динамических рядов и позволяет выявить скорость и интенсивность развития явления, представленного данным рядом. В таблице 6.1 приведены результаты расчета описательных характеристик динамики на примере ежемесячной динамики экспорта Российской Федерации в 2009 году.
Таблица 1
Описательные характеристики динамики экспорта
Российской Федерации
| Месяц | Экспорт товаров, млн. долл. США | Абсолютный прирост, млн. долл. США | Темп роста, % | Темп прироста, % | |||
| Цепной | Базисный | Цепной | Базисный | Цепной | Базисный | ||
| январь | - | - | - | - | - | - | |
| февраль | 103,3 | 103,3 | 3,3 | 3,3 | |||
| март | 112,6 | 116,3 | 12,6 | 16,3 | |||
| апрель | 101,1 | 117,6 | 1,1 | 17,6 | |||
| май | 107,7 | 126,6 | 7,7 | 26,6 | |||
| июнь | 108,3 | 137,2 | 8,3 | 37,2 | |||
| июль | 107,4 | 147,4 | 7,4 | 47,4 | |||
| август | 103,3 | 152,2 | 3,3 | 52,2 | |||
| сентябрь | 105,8 | 160,9 | 5,8 | 60,9 | |||
| октябрь | 106,2 | 170,9 | 6,2 | 70,9 | |||
| ноябрь | 101,1 | 172,8 | 1,1 | 72,8 | |||
| декабрь | 111,0 | 191,8 | 11,0 | 91,8 | |||
| Средние показатели | 1483,73 |
2. Выявление основной тенденции развития и формирование моделей для анализа и прогнозирования.
При изучении и прогнозировании рядов динамики важной задачей является определение основной тенденции развития, для определения которой используются различные приемы и методы.
Одним из приемов выявления тенденции является метод скользящей средней. Суть метода состоит в замене абсолютных данных средними арифметическими за отдельные периоды. Расчет средних ведется способом скольжения, то есть постепенным исключением из принятого периода скольжения первого уровня и включением следующего.
В таблице 6.2 приведены результаты сглаживания временного ряда методом трехчленной и четырехчленной скользящей средней (на основе данных об экспорте товаров).
Таблица 2
Динамика экспорта Российской Федерации в 2009 г.
и расчет скользящих средних
| Месяц | Экспорт товаров, млн. долл. США | Трехчленные скользящие суммы | Трехчленные скользящие средние | Четырехчленные скользящие средние | Четырехчленные скользящие средние (нецентрированные) | Четырехчленные скользящие средние (центрированные) |
| - | - | - | - | - | ||
| - | 18946,3 | - | 19438,3 | |||
| 19989,0 | 20622,5 | 20030,4 | ||||
| 21372,3 | 22128,3 | 21375,4 | ||||
| 22611,0 | 23510,8 | 22819,5 | ||||
| 24376,3 | 25047,8 | 24279,3 | ||||
| 25889,3 | 26571,8 | 25809,8 | ||||
| 27297,0 | 28071,0 | 27321,4 | ||||
| 28691,3 | 29203,0 | 28637,0 | ||||
| 29916,7 | 30964,3 | 30083,6 | ||||
| 31746,0 | - | - | - | |||
| - | - | - | - |
Взяв данные за три месяца, исчисляем трехчленные суммы, затем среднюю:
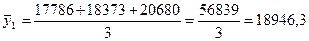 ;
;
 и т.д.
и т.д.
Интервал скольжения можно брать четный (четыре, шесть и т.д.). Нахождение скользящей средней по четному числу членов осложняется тем, что средняя может быть отнесена только к середине между двумя датами. Чтобы ликвидировать этот сдвиг, применяется центрирование, то есть нахождение средней из средних за два периода для отнесения полученного уровня к определенной дате. При центрировании также необходимо находить скользящие суммы.
Наиболее эффективным способом выявления основной тенденции развития является аналитическое выравнивание.
При этом уровни ряда динамики выражаются в виде функции времени:
 .
.
При таком подходе изменение исследуемого показателя связывают лишь с течением времени; считается, что влияние других факторов несущественно или косвенно сказывается через фактор времени.
Правильно выбранная модель кривой роста должна соответствовать характеру изменения тенденции исследуемого явления. Кривая роста позволяет получить выровненные или теоретические значения уровней динамического ряда. Это те уровни, которые наблюдались бы в случае полного совпадения динамики явления с кривой.
Прогнозирование на основе модели кривой роста базируется на экстраполяции, т. е. на продлении в будущее тенденции, наблюдавшейся в прошлом. При этом предполагается, что во временном ряду присутствует тренд, характер развития показателя обладает свойством инерционности, сложившаяся тенденция не должна претерпевать существенных изменений в течение периода упреждения.
В настоящее время в литературе описано несколько десятков кривых роста, многие из которых широко применяются для выравнивания экономических временных рядов: линейная модель, полиномиальная модель второй, третьей степени, логарифмическая, экспоненциальная модели и др.
Существует несколько практических подходов, облегчающих процесс выбора формы кривой роста.
Наиболее простой путь — визуальный анализ, опирающийся на изучение графического изображения временного ряда. Подбирают такую кривую роста, форма которой соответствует фактическому развитию процесса. Если на графике исходного ряда тенденция развития недостаточно четко просматривается, то можно провести некоторые стандартные преобразования ряда (например, сглаживание), а потом подобрать функцию, отвечающую графику преобразованного ряда. В современных пакетах статистической обработки имеется богатый арсенал стандартных преобразований данных и широкие возможности для графического изображения, в том числе в различных масштабах. Все это позволяет существенно упростить для исследователя проведение данного этапа.
В табличном процессоре Microsoft Excel выбор кривой можно осуществить на основании сравнения величины достоверности аппроксимации выбранных моделей: для анализа и прогнозирования необходимо выбрать такую модель, где данная величина будет наибольшей.
Рассмотрим применение метода аналитического выравнивания по прямой ля выражения основной тенденции на следующем примере.
А таблице 2 приведены уже известные данные об экспорте Российской Федерации в 2009 году. Для выравнивания ряда динамики по прямой воспользуемся уравнением 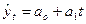 .
.
Способ наименьших квадратов дает систему нормальных уравнений для нахождения параметров 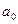 и
и 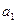 :
:

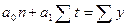 ;
;
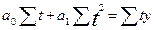 ,
,
где 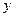 - исходный уровень ряда динамики;
- исходный уровень ряда динамики;
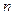 - число членов ряда;
- число членов ряда;
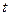 - показатель времени, который обозначается порядковым номером, начиная от низшего (1, 2, 3 и т.д.).
- показатель времени, который обозначается порядковым номером, начиная от низшего (1, 2, 3 и т.д.).
Решение системы позволяет получить выражение для параметров 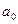 и
и 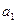 :
:
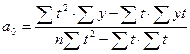 ; (15)
; (15)
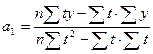 . (16)
. (16)
Расчет необходимых значений приведен в таблице 6.2. По итоговым данным определяем параметры уравнения: 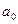 =15 769,
=15 769, 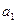 =1 443,2.
=1 443,2.
В результате получаем следующее уравнение основной тенденции экспорта России в 2009 году: 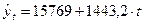
Таблица 3
Исходные и расчетные данные для определения параметров уравнения
| Месяц | Порядковый номер, t | Экспорт, млн. долл. США, y | 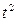
| 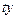
| 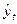
| 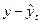
|
| Январь | 17212,2 | 573,8 | ||||
| Февраль | 18655,4 | -282,4 | ||||
| Март | 20098,6 | 581,4 | ||||
| Апрель | 21541,8 | -627,8 | ||||
| Май | -462 | |||||
| Июнь | 24428,2 | -32,2 | ||||
| Июль | 25871,4 | 338,6 | ||||
| Август | 27314,6 | -252,6 | ||||
| Сентябрь | 28757,8 | -138,8 | ||||
| Октябрь | ||||||
| Ноябрь | 31644,2 | -906,2 | ||||
| Декабрь | 33087,4 | 1019,6 | ||||
| Итого | 301 801 | 2 168 088 |
По окончании расчета целесообразно построить график с изображением исходных данных и теоретических значений ряда (рис. 1).
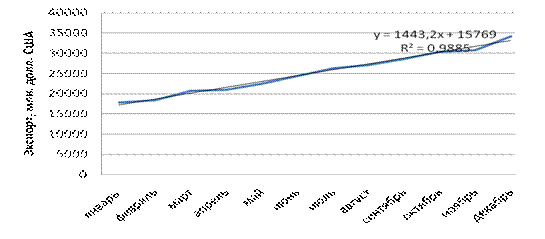
Рис. 1. Графическое изображение исходных данных и теоретических значений по линейной модели
Основная тенденция (тренд) показывает, как воздействуют систематические факторы на уровень ряда динамики, а колеблемость уровней около тренда служит мерой воздействия остаточных факторов.
Оценка качества модели сводится к оценке ее точности и адекватности.
Проверка адекватности выбранных моделей реальному процессу (в частности, адекватности полученной кривой роста) строится на анализе остаточной компоненты. Остаточная компонента получается после выделения из исследуемого ряда систематической составляющей (тренда и периодической составляющей, если она присутствует во временном ряду). В нашем случае исходный временной ряд описывает процесс, не подверженный сезонным колебаниям. Ряд остатков получается как отклонение фактических значений временного ряда от теоретических, полученных по модели (табл. 3):
 . (17)
. (17)
Теоретические значения за каждый период рассчитываются путем подстановки в полученную функцию последовательных значений t.
Принято считать, что модель адекватна описываемому процессу, если остаточная последовательность (ряд остатков) представляет собой случайную компоненту ряда.
Поэтому при оценке «качества» модели проверяют, удовлетворяет ли остаточная последовательность следующим свойствам:
1) случайности колебаний уровней ряда;
2) соответствию распределения остаточной компоненты нормальному закону с нулевым математическим ожиданием;
3) независимости значений уровней ряда остатков между собой.
При проверке первого свойства исследователю полезно провести графический анализ остаточной последовательности.
В современных эконометрических пакетах имеется набор графических средств, позволяющих судить о том, насколько распределение остатков согласуется с нормальным распределением. Например, полезным может оказаться график гистограммы остатков с наложенной нормальной плотностью, позволяющей исследователю оценить симметричность распределения остатков и близость к нормальному закону.
Кроме графических средств, в современных пакетах прикладных программ представлены и статистические критерии, позволяющие проводить проверку гипотезы о нормальности распределения остатков, например, критерий Пирсона и др. Однако на практике использование этих средств зачастую затруднено из-за небольшой длины временных рядов экономических показателей (n < 50). Поэтому проверка на нормальность может быть произведена приближенно, например, на основе подхода, опирающегося на рассмотрение показателей асимметрии и эксцесса.
Как известно, при нормальном распределении показатели асимметрии и эксцесса равны нулю. Так как мы предполагаем, что отклонения от тренда представляют собой выборку из некоторой генеральной совокупности, то можно определить выборочные характеристики асимметрии (А) и эксцесса (Э), а также оценить их среднеквадратические ошибки, зависящие от длины ряда n:
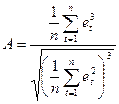 ,
, 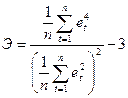 . (18)
. (18)
Если одновременно выполняются следующие неравенства:
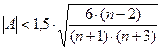 , (19)
, (19)
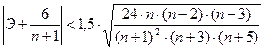 , (20)
, (20)
то гипотеза о нормальном характере распределения случайной компоненты не отвергается.
Если выполняется хотя бы одно из неравенств:
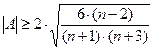 , (21)
, (21)
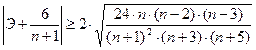 , (22)
, (22)
то гипотеза о нормальном характере распределения отвергается.
Другие случаи требуют дополнительной проверки с помощью более мощных критериев.
Рассмотрим подробнее последнее свойство. Если вид функции, описывающей систематическую составляющую, выбран неудачно, то последовательные значения ряда остатков могут не обладать свойствами независимости, т.к. они могут коррелировать между собой. В этом случае говорят, что имеет место автокорреляция остатков.
Существует несколько приемов обнаружения автокорреляции. Наиболее распространенным является подход, опирающийся на критерий Дарбина-Уотсона. Тест Дарбина-Уотсона связан с проверкой гипотезы об отсутствии автокорреляции первого порядка, т.е. автокорреляции между соседними остаточными членами ряда. При этом критическая статистика определяется по формуле:
 . (23)
. (23)
Можно показать, что величина d приближенно равна:
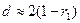 , (24)
, (24)
где 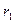 — коэффициент автокорреляции первого порядка (то есть парный коэффициент корреляции между двумя последовательностями остатков
— коэффициент автокорреляции первого порядка (то есть парный коэффициент корреляции между двумя последовательностями остатков 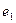 ,
, 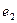 ,…,
,…,  и
и 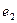 ,
, 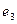 , …,
, …, 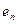 . Близость значения статистики d к нулю означает наличие высокой положительной автокорреляции (коэффициент
. Близость значения статистики d к нулю означает наличие высокой положительной автокорреляции (коэффициент 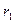 близок к единице); близость значения статистики d к четырем означает наличие высокой отрицательной автокорреляции (коэффициент
близок к единице); близость значения статистики d к четырем означает наличие высокой отрицательной автокорреляции (коэффициент 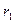 близок к минус единице). Естественно, в случае отсутствия автокорреляции значение статистики d будет близким к двум (коэффициент
близок к минус единице). Естественно, в случае отсутствия автокорреляции значение статистики d будет близким к двум (коэффициент 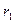 не сильно отличается от нуля).
не сильно отличается от нуля).
Применение на практике критерия Дарбина-Уотсона основано на сравнении расчетного значения статистики d с пороговыми, граничными значениями 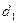 и
и 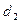 .
.
Граничные значения 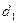 и
и 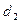 , зависящие от числа наблюдений n, количества объясняющих переменных в модели, уровня значимости α, находятся по таблицам (авторами критерия составлены таблицы для α = 0,05, α = 0,025 и α = 0,01). Фрагмент таблицы Дарбина-Уотсона с критическими значениями
, зависящие от числа наблюдений n, количества объясняющих переменных в модели, уровня значимости α, находятся по таблицам (авторами критерия составлены таблицы для α = 0,05, α = 0,025 и α = 0,01). Фрагмент таблицы Дарбина-Уотсона с критическими значениями 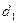 и
и 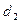 при 5% уровне значимости представлен ниже (см. табл. 3).
при 5% уровне значимости представлен ниже (см. табл. 3).
Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий. Выдвигается гипотеза 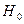 об отсутствии автокорреляции остатков. Пусть альтернативная гипотеза состоит в наличии в остатках положительной автокорреляции первого порядка.
об отсутствии автокорреляции остатков. Пусть альтернативная гипотеза состоит в наличии в остатках положительной автокорреляции первого порядка.
Тогда при сравнении расчетного значения статистики d ( d < 2) с 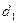 и
и 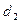 возможны следующие варианты.
возможны следующие варианты.
1) если d < 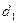 , то гипотеза
, то гипотеза 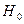 об отсутствии автокорреляции отвергается (с вероятностью ошибки, равной α ) в пользу гипотезы о положительной автокорреляции;
об отсутствии автокорреляции отвергается (с вероятностью ошибки, равной α ) в пользу гипотезы о положительной автокорреляции;
2) если d > 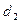 , то гипотеза
, то гипотеза 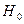 не отвергается;
не отвергается;
3) если 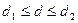 , то нельзя сделать определенный вывод по имеющимся исходным данным (значение d попало в область неопределенности).
, то нельзя сделать определенный вывод по имеющимся исходным данным (значение d попало в область неопределенности).
Если альтернативной является гипотеза о наличии в остатках отрицательной автокорреляции первого порядка, то с пороговыми, граничными значениями 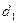 и
и 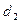 сравнивается величина 4 − d (при d >2).
сравнивается величина 4 − d (при d >2).
При этом возможны следующие варианты.
1) если 4 − d < 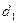 , то гипотеза
, то гипотеза 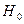 об отсутствии автокорреляции отвергается (с вероятностью ошибки, равной α) в пользу гипотезы об отрицательной автокорреляции;
об отсутствии автокорреляции отвергается (с вероятностью ошибки, равной α) в пользу гипотезы об отрицательной автокорреляции;
2) если 4 − d > 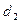 , то гипотеза
, то гипотеза 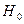 не отвергается;
не отвергается;
3) если 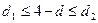 , то нельзя сделать определенный вывод по имеющимся исходным данным.
, то нельзя сделать определенный вывод по имеющимся исходным данным.
Таблица 3
Значения 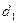 и
и 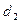 критерия Дарбина-Уотсона при 5% уровне значимости ( n – длина временного ряда, К – число объясняющих переменных в модели)
критерия Дарбина-Уотсона при 5% уровне значимости ( n – длина временного ряда, К – число объясняющих переменных в модели)
| n | К=1 | К=2 | К=3 | |||
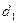
| 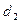
| 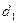
| 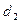
| 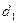
| 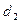
| |
| 1,08 | 1,36 | 0,95 | 1,54 | 0,82 | 1,75 | |
| 1,1 | 1,37 | 0,98 | 1,54 | 0,86 | 1,73 | |
| 1,13 | 1,38 | 1,02 | 1,54 | 0,9 | 1,71 | |
| 1,16 | 1,39 | 1,05 | 1,53 | 0,93 | 1,69 | |
| 1,18 | 1,4 | 1,08 | 1,53 | 0,97 | 1,68 | |
| 1,2 | 1,41 | 1,1 | 1,54 | 1,68 | ||
| 1,22 | 1,42 | 1,13 | 1,54 | 1,03 | 1,67 | |
| 1,”4 | 1,43 | 1,15 | 1,54 | 1,05 | 1,66 | |
| 1,26 | 1,44 | 1,17 | 1,54 | 1,08 | 1,66 | |
| 1,27 | 1,45 | 1,19 | 1,55 | 1,1 | 1,66 | |
| 1,29 | 1,45 | 1,21 | 1,55 | 1,12 | 1,66 | |
| 1,3 | 1,46 | 1,22 | 1,55 | 1,14 | 1,65 | |
| 1,32 | 1,47 | 1,24 | 1,56 | 1,16 | 1,65 | |
| 1,33 | 1,48 | 1,26 | 1,56 | 1,18 | 1,65 | |
| 1,34 | 1,48 | 1,27 | 1,56 | 1,2 | 1,65 | |
| 1,35 | 1,49 | 1,28 | 1,57 | 1,21 | 1,65 | |
| 1,36 | 1,5 | 1,3 | 1,57 | 1,23 | 1,65 | |
| 1,37 | 1,5 | 1,31 | 1,57 | 1,24 | 1,65 | |
| 1,38 | 1,51 | 1,32 | 1,58 | 1,26 | 1,65 | |
| 1,49 | 1,51 | 1,33 | 1,58 | 1,27 | 1,65 | |
| 1,4 | 1,52 | 1,34 | 1,58 | 1,28 | 1,65 | |
| 1,41 | 1,52 | 1,35 | 1,59 | 1,29 | 1,65 |
Таким образом, можно считать, что в случае отсутствия автокорреляции в остатках расчетное значение статистики «не слишком отличается» от 2.
Важнейшими характеристиками качества модели, выбранной для прогнозирования, являются показатели ее точности. Они описывают величины случайных ошибок, полученных при использовании модели. Таким образом, чтобы судить о качестве выбранной модели, необходимо проанализировать систему показателей, характеризующих как адекватность модели, так и ее точность.
О точности прогноза можно судить по величине ошибки (погрешности) прогноза. Ошибка прогноза — величина, характеризующая расхождение между фактическим и прогнозным значением показателя.
Абсолютная ошибка прогноза определяется по формуле:
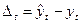 , (25)
, (25)
где 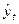 - прогнозное значение показателя,
- прогнозное значение показателя,
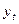 - фактическое значение.
- фактическое значение.
Эта характеристика имеет ту же размерность, что и прогнозируемый показатель, и зависит от масштаба измерения уровней временного ряда.
На практике широко используется относительная ошибка прогноза, выраженная в процентах относительно фактического значения показателя:
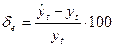 (26)
(26)
При проведении сравнительной оценки моделей могут использоваться такие характеристики качества как дисперсия (S2) или среднеквадратическая ошибка (S):
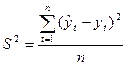 ;
; 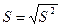 . (27)
. (27)
Чем меньше значения этих характеристик, тем выше точность модели.
В указанном выше примере коэффициенты асимметрии и эксцесса равны соответственно 0,0047 и (-0,77), гипотеза о нормальном характере распределения случайной компоненты не отвергается.
Проверив остатки на автокорреляцию, получаем критерий Дарбина – Уотсона 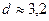 ; d >
; d > 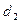 , гипотеза
, гипотеза 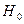 об отсутствии автокорреляции не отвергается, можно сделать вывод о независимости значений уровней ряда остатков между собой. Следовательно, выбранная модель адекватна по рассмотренным критериям.
об отсутствии автокорреляции не отвергается, можно сделать вывод о независимости значений уровней ряда остатков между собой. Следовательно, выбранная модель адекватна по рассмотренным критериям.
Среднеквадратическая ошибка прогноза составляет 536 млн. долл. США или 3 % от среднего значения экспорта Российской Федерации. Модель является достаточно точной и может быть использована для описания основной тенденции и прогнозирования.
В случае если исследователь рассматривает в качестве альтернативы другие модели, для экстраполяции тенденции на будущие периоды необходимо выбрать адекватную модель с наименьшими значениями ошибок.
3. Прогнозирование на основе анализа временных рядов.
Заключительным этапом применения кривых роста является экстраполяция тенденции на базе выбранного уравнения. Прогнозные значения исследуемого показателя вычисляют путем подстановки в уравнение кривой значений времени t, соответствующих периоду упреждения. Полученный таким образом прогноз называют точечным ( 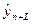 ), так как для каждого момента времени определяется только одно значение прогнозируемого показателя.
), так как для каждого момента времени определяется только одно значение прогнозируемого показателя.
На практике в дополнении к точечному прогнозу желательно определить границы возможного изменения прогнозируемого показателя, задать «вилку» возможных значений прогнозируемого показателя, т.е. вычислить прогноз интервальный. Интервал, в котором будет находиться точечный прогноз, называется доверительным.
 , (28)
, (28)
где 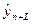 - точечный прогноз на момент n+L;
- точечный прогноз на момент n+L;
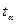 – значение t-статистики Стьюдента;
– значение t-статистики Стьюдента;
n – длина временного ряда;
L – период упреждения прогноза;
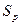 – среднеквадратическая ошибка прогноза.
– среднеквадратическая ошибка прогноза.
Так как оценки параметров определяются по выборочной совокупности, представленной временным рядом, то они содержат погрешность. Погрешность параметров приводит к вертикальному сдвигу прямой и изменению угла наклона прямой относительно оси абсцисс. С учетом разброса конкретных реализаций относительно линий тренда, доверительный интервал можно представить в виде:
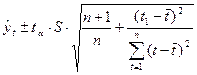 , (29)
, (29)
S - среднеквадратическое отклонение фактических значений от расчетных;
n – длина временного ряда;
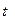 - порядковый номер уровней ряда;
- порядковый номер уровней ряда;
 - время упреждения, для которого делается экстраполяция,
- время упреждения, для которого делается экстраполяция,  ;
;
 - порядковый номер уровня ряда, стоящего в середине ряда,
- порядковый номер уровня ряда, стоящего в середине ряда,  .
.
Существуют табличные значения для выражения 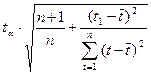 (см. табл. 6.4).
(см. табл. 6.4).
Точечный прогноз экспорта России на февраль (период упреждения – 2, t=14) 2010 по данной модели составит:
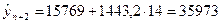 млн. долл. США.
млн. долл. США.
Интервальный прогноз стоимостного объема экспорта Российской Федерации на основе линейного тренда при доверительной вероятности 0,9 в феврале 2010 составит:
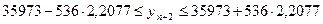 ,
,
 .
.
Без статистической оценки невозможно объективно сделать анализ и прогнозирование социально-экономического явления, в том числе в таможенной сфере. В то же время нельзя допустить, чтобы на первый план выходили статистические методы без подкрепления содержательной базой, описывающей исследуемое социально-экономическое явление во внешней торговле.
Таблица 4
Табличные значения для оценки доверительных интервалов прогноза на основе линейного тренда при доверительной вероятности 0,9
| Длина временного ряда, n | Длина упреждения прогноза | ||
| 2,6380 | 2,8748 | 3,1399 | |
| 2,4631 | 2,6391 | 2,8361 | |
| 2,3422 | 2,4786 | 2,6310 | |
| 2,2524 | 2,3614 | 2,4827 | |
| 2,1827 | 2,2718 | 2,3706 | |
| 2,1274 | 2,2017 | 2,2836 | |
| 2,0837 | 2,1463 | 2,2155 | |
| 2,0462 | 2,1000 | 2,1590 | |
| 2,0153 | 2,0621 | 2,1131 | |
| 1,9883 | 2,0292 | 2,0735 | |
| 1,9654 | 2,0015 | 2,0406 | |
| 1,9455 | 1,9776 | 2,0124 | |
| 1,9280 | 1,9568 | 1,9877 | |
| 1,9117 | 1,9375 | 1,9654 | |
| 1,8975 | 1,9210 | 1,9461 | |
| 1,8854 | 1,9066 | 1,9294 | |
| 1,8738 | 1,8932 | 1,9140 | |
| 1,8631 | 1,8808 | 1,8998 | |
| 1,8538 | 1,8701 | 1,8876 |
Всегда в оценке результатов и прогнозировании необходимо опираться на социально-экономическую интерпретацию исследуемого явления. Так, при прогнозировании объемов экспорта Российской Федерации следует учитывать сложное состояние экономики в условиях финансово-экономического кризиса, затронувшего всю мировую экономику. В подобных условиях прогнозное значение может оказаться ниже предполагаемого по линейной модели, представленной в данной главе.
Дата добавления: 2017-09-19; просмотров: 1961;
