Тема. Показатели и анализ вариации
Вопросы:
1. Понятие вариации. Абсолютные показатели вариации.
2. Относительные показатели вариации.
3. Дисперсия. Виды дисперсии
4. Эмпирическое корреляционное отношение.
5. Показатели формы распределения.
1. Понятие вариации. Абсолютные показатели вариации
Вариация — это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.
Например, работники фирмы различаются по доходам, затратам времени на работу, уровню образования, уровню квалификации и т.д. Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае.
Показатели вариации являются числовой мерой уровня колеблемости признака. Чем больше варианты отдельных единиц совокупности различаются между собой, тем больше они отличаются от своей средней, и наоборот, — чем меньше варианты отличаются друг от друга, тем меньше они отличаются от средней, которая в таком случае будет более реально представлять всю совокупность. Вот почему ограничиваться вычислением одной средней в ряде случаев нельзя. Нужны и другие показатели, характеризующие отклонения отдельных значений от средней.
В статистике применяют ряд обобщающих показателей вариации. .
К абсолютным показателям вариации относятся: размах вариации, среднее линейное отклонение,дисперсия и среднее квадратическое отклонение, квартильное отклонение. Для оценки интенсивности вариации и для сравнения ее в разных совокупностях используют относительные показатели вариации: коэффициент осцилляции, относительное линейное отклонение, коэффициент вариации.
Самым элементарным показателем вариации признака является размах вариации, представляющий собой разность между максимальным и минимальным значениями признака:
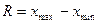 . (1)
. (1)
Величина размаха характеризует лишь максимальное различие значений признака.
Показателем вариации выступает среднее линейное отклонение. Этот показатель рассчитывается по формуле для несгруппированных данных
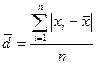 , (2)
, (2)
для сгруппированных данных
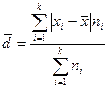 . (3)
. (3)
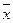 - среднее значение признака,
- среднее значение признака,
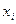 - i значение признака (варианта),
- i значение признака (варианта),
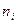 - частот i варианты,
- частот i варианты,
п – объем совокупности.
Среднее линейное отклонение нельзя поставить в соответствие, с каким- либо вероятностным законом, в том числе и с нормальным распределением, параметром которого является среднее квадратическое отклонение.
Расчет среднего квадратического отклонения проводится по формулам: для несгруппированных данных
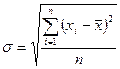 , (4)
, (4)
для сгруппированных данных
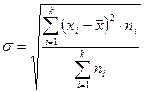 . (5)
. (5)
Среднее квадратическое отклонение по величине в реальных совокупностях всегда больше среднего линейного отклонения. Соотношение 
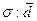 зависит от наличия в совокупности резких, выделяющихся отклонений и может служить индикатором «засоренности» совокупности неоднородными элементами: чем это соотношение больше, тем сильнее подобная «засоренность». Для нормального закона распределения
зависит от наличия в совокупности резких, выделяющихся отклонений и может служить индикатором «засоренности» совокупности неоднородными элементами: чем это соотношение больше, тем сильнее подобная «засоренность». Для нормального закона распределения 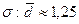 .
. 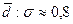 Среднее квадратическое отклонение — это обобщающая характеристика размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения; является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому экономически хорошо интерпретируется.
Среднее квадратическое отклонение — это обобщающая характеристика размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения; является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому экономически хорошо интерпретируется.
Квадрат среднего квадратического отклонения дает величину дисперсии s2. Формула дисперсии:
Для сгруппированных данных 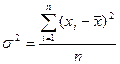 . (6)
. (6)
Для не сгруппированных данных 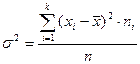 . (7)
. (7)
Простыми преобразованиями могут быть получены формулы расчета дисперсии методом моментов 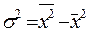 .Расчет по этой формуле дает равенство результатов с (7) при точном значении средней арифметической величины. Если средняя округлена, то приведет к погрешности результатов.
.Расчет по этой формуле дает равенство результатов с (7) при точном значении средней арифметической величины. Если средняя округлена, то приведет к погрешности результатов.
Еще одним показателем силы вариации, характеризующим ее не по всей совокупности, а лишь в центральной части, служит среднее квартальное расстояние, т.е. средняя величинаразности между квартилями, обозначаемое далее как q:
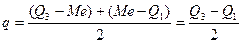 . (8)
. (8)
Сила вариации в центральной части совокупности, как правило, меньше, чем в целом по всей совокупности. Соотношение между средним линейным отклонением и средним квартильным отклонением также служит для изучения структуры вариации: большое значение такого соотношения говорит о наличии слабо варьирующего «ядра» и сильно рассеянного вокруг этого ядра окружения. Например, d:q=1,23, что говорит о небольшом различии силы вариации в центральной части совокупности и на ее периферии.
Под альтернативным понимается такой статистический показатель, который принимает одно из двух возможных значений (пол – женский или мужской, изделие годное или негодное, план по выпуску продукции - выполнен или не выполнен). Конкретное содержание альтернативного признака устанавливается самим исследователем. Обозначим: 1 — наличие интересующего нас признака; 0 — его отсутствие; р — доля единиц, обладающих данным признаком; q — доля единиц, не обладающих данным признаком; р + q=1. Расчет среднего значения альтернативного признака и среднее квадратическое отклонение альтернативного признака проводят по формулам:
среднее значение альтернативного признака
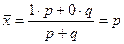 , (9)
, (9)
среднее квадратическое отклонение альтернативного признака
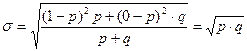 . (10)
. (10)
2. Относительные показатели вариации
Для оценки интенсивности вариации и для сравнения ее в разных совокупностях и тем более для разных признаков необходимыотносительные показатели вариации.Они вычисляютсякак отношения абсолютных показателей силы вариации, рассмотренных ранее, к средней арифметической величине признака. Рассчитываются следующие показатели:
1) относительный размах вариации VR (коэффициент осцилляции):
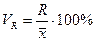 (11)
(11)
2) линейный коэффициент вариации:
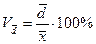 (12)
(12)
3) коэффициент вариации
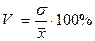 (13)
(13)
4) относительное квартальное расстояние:
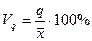 (14)
(14)
Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. Совокупность считается количественно однородной и средняя является типичной характеристикой для данной совокупности, если коэффициент вариации не превышает 33 %.
Пример.
Имеются следующие исходные данные по отдельным коммерческим банкам РФ за отчетный год:
Таблица 1
Данные о собственном капитале банков региона
| Номер банка | Собственный капитал, млн. руб. |
| 335,2 | |
| 377,2 | |
| 355,1 | |
| 404,7 | |
| 406,2 | |
| 406,2 | |
| 442,3 | |
| 507,3 | |
| 534,7 | |
| 544,4 | |
| 642,7 | |
| 665,2 | |
| 769,7 | |
| 796,9 | |
| 834,6 | |
| 870,2 |
На основании представленных данных рассчитать показатели вариации.
Абсолютные показатели:
1) размах вариации: (R)
R=Xmax-Xmin,
где Xmax и Xmin – максимальное и минимальное значения признака соответственно. Так как данные проранжированы в порядке возрастания, то имеем:
R = 870,2 – 335,2 = 535,0 (млн. руб.)
2) среднее линейное отклонение ( 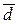 ):
):
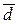 =
= 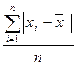 ,
,
где xi – индивидуальные значения признака;
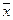 средняя арифметическая величина.
средняя арифметическая величина.
Значение 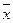 рассчитывается по следующей формуле:
рассчитывается по следующей формуле: 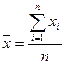 , где n – число банков.
, где n – число банков.
Расчет показателей представим в таблице 6.2.:
Таблица 2
Исходные данные для расчета показателей вариации
| N п/п | Xi | |хi – 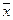 | |
| Xi2 |
| 335,2 | 230,69 | 112359,04 | |
| 377,2 | 228,69 | 113703,84 | |
| 355,1 | 210,79 | 126096,01 | |
| 404,7 | 161,19 | 163782,09 | |
| 406,2 | 159,69 | 164998,44 | |
| 442,3 | 123,59 | 195629,29 | |
| 507,3 | 58,59 | 257353,29 | |
| 534,7 | 31,19 | 285904,09 | |
| 544,4 | 21,49 | 296371,36 | |
| 642,7 | 76,81 | 413063,29 | |
| 665,7 | 99,81 | 443156,49 | |
| 665,7 | 99,81 | 443156,49 | |
| 769,7 | 203,81 | 592438,09 | |
| 796,9 | 230,81 | 634730,89 | |
| 834,6 | 268,71 | 696557,16 | |
| 870,2 | 304,31 | 757248,04 | |
| Итого | 8488,4 | 2410,17 | 5253391,41 |
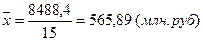
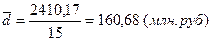
3) Дисперсия (s2):
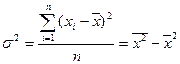
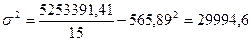
4) Среднее квадратическое отклонение (s):
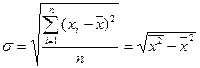
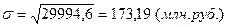
Относительные показатели:
1) Коэффициент осцилляции (VR):
VR = 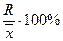
VR = 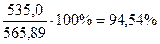
2) Линейный коэффициент вариации 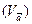 :
:
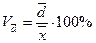
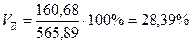
3) Коэффициент вариации (V):
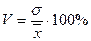
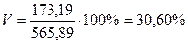
На основании проведенных расчетов можно сделать следующие основные выводы:
- в среднем индивидуальные значения признака отклоняются от средней арифметической на 160,68 млн. руб. по среднему линейному отклонению и на 173,19 млн. руб. по среднему квадратическому отклонению;
- данные по собственному капиталу банков являются достаточно однородными (коэффициент вариации не превышает 33%) и, следовательно, средняя арифметическая будет типичной, надежной оценкой по исследуемому признаку.
3. Дисперсия. Виды дисперсии
Вариация признака обусловлена различными факторами, некоторые из этих факторов можно выделить, если статистическую совокупность разбить на группы по какому-либо признаку, то есть построить аналитическую группировку. Тогда, наряду с изучением вариации признака по всей совокупности в целом, становится возможным изучить вариацию для каждой из составляющих ее группы, а также и между этими группами.
Дисперсия результативного признака внутри группы при относительном постоянстве признака-фактора возникает за счет других факторов (не связанных с изучаемым). Такая дисперсия называется остаточной (та колеблемость, которая осталась при закреплении изучаемого фактора ).
Межгрупповая дисперсия относится на счет изучаемого фактора (и факторов, связанных с ним), поэтому называется факторной.
В простейшем случае, когда совокупность расчленена на группы по одному фактору, изучение вариации достигается посредством исчисления и анализа трех видов дисперсий: общей, межгрупповой и внутри групповой.
Общая дисперсия s2 измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений признака Х- от общей средней 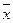 и может быть вычислена как простая дисперсия или взвешенная дисперсия по формуле (6) или (7).
и может быть вычислена как простая дисперсия или взвешенная дисперсия по формуле (6) или (7).
Межгрупповая дисперсия d2 характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних 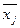 , от общей средней
, от общей средней 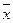 . Межгрупповая дисперсия вычисляется по формуле:
. Межгрупповая дисперсия вычисляется по формуле:
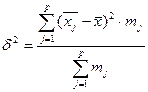 (15)
(15)
где mj - численность единиц в группе,
j – номер группы,
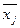 - среднее значение признака в j группе,
- среднее значение признака в j группе,
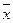 - общая средняя.
- общая средняя.
Внутригрупповая (частная) дисперсия 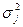 , отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы
, отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы 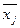 (групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно:
(групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно:
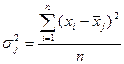 ,
, 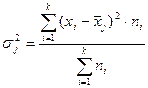 , (16)
, (16)
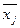 - среднее значение признака в j группе,
- среднее значение признака в j группе,
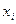 - i значение признака (варианта),
- i значение признака (варианта),
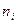 - частот i варианты,
- частот i варианты,
п – объем совокупности.
На основании внутри групповой дисперсии по каждой группе, т.е. на основании 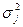 можно определить общую среднюю из внутригрупповых дисперсий
можно определить общую среднюю из внутригрупповых дисперсий 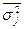 :
:
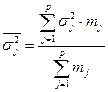 . (17)
. (17)
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:
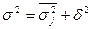 . (18)
. (18)
Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью — неизвестную, а также судить о силе влияния группировочного признака.
Очевидно, чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака на изучаемый признак.
Поэтому в статистическом анализе широко используется эмпирический коэффициент детерминации (h2) — показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:
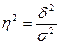 (19)
(19)
Эмпирический коэффициент детерминации показывает долю вариации результативного признака у под влиянием факторного признака х (остальная часть общей вариации у обуславливается вариацией прочих факторов). При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной связи - единице.
Эмпирическое корреляционное отношение — это корень квадратный из эмпирического коэффициента детерминации: 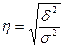
оно показывает тесноту связи между группировочным и результативным признаками.
Эмпирическое корреляционное отношение h, как и h2, может принимать значения от 0 до 1.
Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации.
Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна обшей дисперсии ( 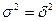 ), т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака.
), т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака.
Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.
Для качественной оценки тесноты связи на основе показателя эмпирического корреляционного отношения можно воспользоваться соотношениями Чэддока:
| hэ | 0,1-0,3 | 0,3-0,5 | 0,5-0,7 | 0,7-0,9 | 0,9-0,99 |
| Сила связи | Слабая | Умеренная | Заметная | Тесная | Весьма тесная |
Пример.
Имеются следующие данные о величине кредитов, выданных частным лицам, российскими и иностранными банками, функционирующими на территории РФ:
Таблица 3
| Банки | Выдано кредитов частным лицам, млн. руб. |
| Российские | 2557,3; 2025,1; 1682,2; 1608,5; 1346,3; 1340,2; 1312,4; 1308,6 |
| Иностранные | 410,1; 273,2; 187,5; 148,1 |
На основании приведенных данных проверить правило сложения дисперсий и определить влияние факторного признака на вариацию величины кредитов, выданных частным лицам.
Решение.
Проанализируем вариацию кредитов частным лицам по всем банкам. Для этого рассчитаем общую дисперсию по следующей формуле:
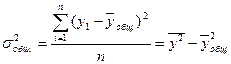 ,
,
где 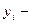 значение признака по каждой единице;
значение признака по каждой единице;
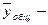 общая средняя, рассчитанная по всем единицам.
общая средняя, рассчитанная по всем единицам.
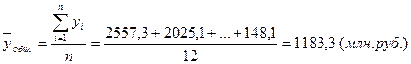
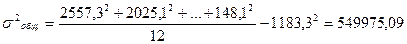
Общая дисперсия характеризует вариацию объема кредитов частным лицам под влиянием всех факторов. Однако из таблицы видно, что вариация объема кредитов частным лицам зависит прежде всего от факторного признака.
Построим групповую таблицу, полученную по результатам аналитической группировки:
Таблица 4
| Банки | Число банков, nj | Средний объем кредитов частным лицам, 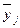
| Дисперсия объема кредитов частным лицам в группе, s2j |
| Российские | 1647,6 | 173186,45 | |
| Иностранные | 254,7 | 10105,44 | |
| Итого |
По каждой группе рассчитывается внутригрупповая дисперсия, характеризующая вариацию объема кредитов частным лицам под влиянием всех прочих случайных факторов (кроме фактора, положенного в основу группировки), по следующей формуле:
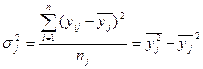 ,
,
где j =1¸k (номер группы)
i = 1¸n (номер единицы)
Таким образом, имеем:
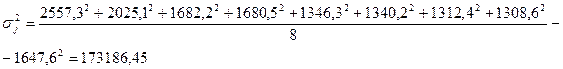
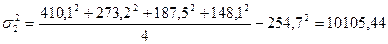
В целом для всех единиц рассчитывается средняя из внутригрупповых дисперсий:
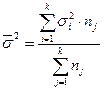
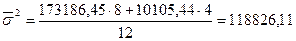
Для оценки вариации объема кредитов частным лицам под влиянием факторного признака рассчитаем межгрупповую дисперсию:
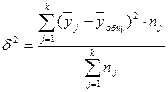
Общую среднюю ( 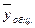 ) определим по следующей формуле:
) определим по следующей формуле:
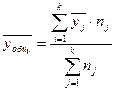
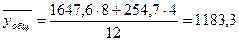 (млн. руб.)
(млн. руб.)
Тогда 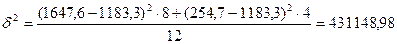
Общая дисперсия представляет собой сумму межгрупповой и средней из внутригрупповых дисперсий:
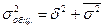
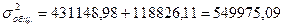 , что соответствует общей дисперсии, рассчитанной выше.
, что соответствует общей дисперсии, рассчитанной выше.
Для оценки влияния факторного признака на вариацию объема кредитов частным лицам рассчитаем долю межгрупповой дисперсии в общей, которая называется коэффициентом детерминации (h2):
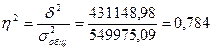 (78,4%)
(78,4%)
Следовательно, на 78,4 % вариация объема кредитов частным лицам зависит от факторного признака и на 21,6 % (100-78,4) – от влияния всех прочих факторов.
Таким образом, в сочетании с методом группировок правило сложения дисперсий позволяет выявить факторы, оказывающие наибольшее влияние на вариацию признака в совокупности и дать количественную оценку степени влияния этих факторов.
5. Показатели формы распределения
Для дальнейшего изучения характера вариации используются средние значения разных степеней отклонений отдельных величин признака от его средней арифметической величины. Эти показатели получили название центральных моментов распределения порядка, соответствующего степени, в которую возводятся отклонения, или начальных моментов.
Согласно свойству средней арифметической центральный момент первого порядка равен нулю, второй центральный момент представляет собой дисперсию. Величина третьего момента зависит, как и его знак, от преобладания положительных отклонений в кубе над отрицательными либо наоборот.
При нормальном и любом другом строго симметричном распределении сумма положительных отклонений в кубе строго равна сумме отрицательных отклонений в кубе. Центральный момент третьего порядка используется при оценке асимметрии. Четвертый момент используется для оценки эксцесса.
Центральные моменты
| Порядок момента | Формула | |
| по не сгруппированным данным | по сгруппированным данным | |
Первый
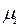
| 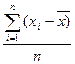
| 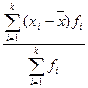
|
Второй
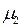
| 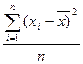
| 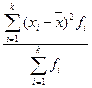
|
Третий
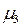
| 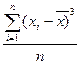
| 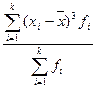
|
Четвертый
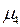
| 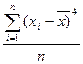
| 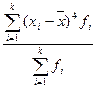
|
Показатели формы распределения:
Асимметрия(As) показатель характеризующий степень асимметричности распределения.
Английский статистик К. Пирсон на основе разности между средней величиной и модой предложил расчет показателя асимметрии.
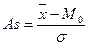
Следовательно, при (левосторонней) отрицательной асимметрии 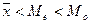 . При (правосторонней) положительной асимметрии
. При (правосторонней) положительной асимметрии 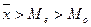 .
.
Графически правосторонняя и левосторонняя асимметрия представлена на рисисунке 6.1.

Рис. 1. Графики асимметричности распределения.
Для расчета асимметрии можно использовать центральные моменты. Тогда:
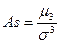 ,
,
где μ3 – центральный момент третьего порядка.
Показатель Пирсона зависит от степени асимметрии в средней части ряда распределения, а показатель асимметрии, основанный на моменте третьего порядка, от крайних значений признака.
- эксцесс (Ек) характеризует крутизну графика функции в сравнении с с нормальным распределением при той же силе вариации:
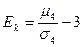 ,
,
где μ4 – центральный момент 4-ого порядка, определяемый по формуле:


Для построения кривой нормального распределения используются два параметра: средняя арифметическая и среднее квадратическое отклонение.
По показателям асимметрии и эксцесса распределения можно судить о близости распределения к нормальному. Распределение можно считать нормальным, если показатели асимметрии и эксцесса не превышают своих двукратных средних квадратических отклонений, рассчитанных по формулам:
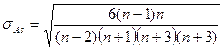
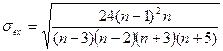
Если отношение 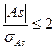 ,
, 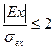 ,то асимметрия является незначительной, распределение можно считать нормальным.
,то асимметрия является незначительной, распределение можно считать нормальным.
Дата добавления: 2017-09-19; просмотров: 1381;
