Частные производные ФНП
Рассмотрим линию 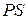 пересечения поверхности
пересечения поверхности 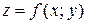 с плоскостью
с плоскостью 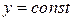 , параллельной плоскости
, параллельной плоскости 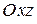 . Так как в этой плоскости
. Так как в этой плоскости 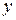 сохраняет постоянное значение, то
сохраняет постоянное значение, то 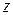 вдоль кривой
вдоль кривой 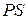 будет меняться только в зависимости от изменения
будет меняться только в зависимости от изменения 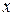 . Дадим независимой переменной
. Дадим независимой переменной 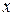 приращение
приращение 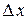 , тогда
, тогда 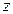 получит приращение, которое называется частным приращением
получит приращение, которое называется частным приращением 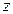 по
по 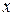 и обозначают через
и обозначают через 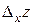 (на рисунке отрезок
(на рисунке отрезок 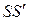 ), так что
), так что
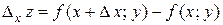 .
.
Аналогично, если 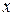 сохраняет постоянное значение, а
сохраняет постоянное значение, а 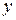 получает приращение
получает приращение
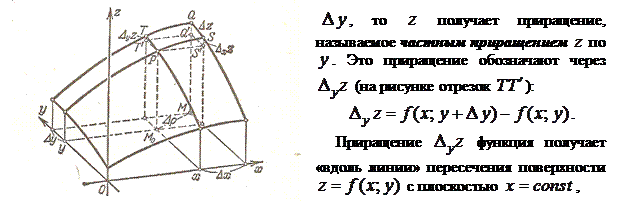
параллельной плоскости 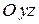 .
.
Наконец, придав аргументу 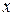 приращение
приращение 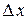 , а аргументу
, а аргументу 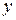 приращение
приращение 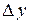 , получим для
, получим для 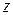 новое приращение
новое приращение 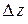 , которое называется полным приращением функции
, которое называется полным приращением функции 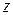 и определяется формулой
и определяется формулой
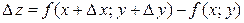 .
.
На рисунке 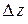 изображено отрезком
изображено отрезком 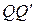 .
.
Надо отметить, что, вообще говоря, полное приращение не равно сумме частных приращений, т.е. 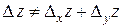 .
.
Определение 2.1. Частной производной по 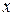 от функции
от функции 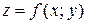 называется предел отношения частного приращения
называется предел отношения частного приращения 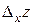 по
по 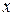 к приращению
к приращению 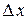 при стремлении
при стремлении 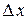 к нулю. Обозначается:
к нулю. Обозначается: 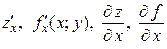 . Тогда
. Тогда
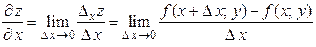 . (2.1)
. (2.1)
Определение 2.2. Частной производной по 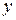 от функции
от функции 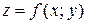 называется предел отношения частного приращения
называется предел отношения частного приращения 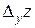 по
по 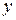 к приращению
к приращению 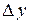 при стремлении
при стремлении 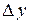 к нулю. Обозначается:
к нулю. Обозначается: 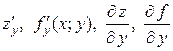 . Тогда
. Тогда
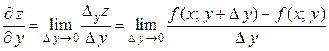 . (2.2)
. (2.2)
Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции 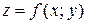 находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно
находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно 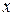 или
или 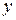 считаются постоянной величиной).
считаются постоянной величиной).
Геометрический смысл частных производных: частная производная 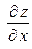 численно равна тангенсу угла наклона a касательной к сечению поверхности
численно равна тангенсу угла наклона a касательной к сечению поверхности 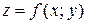 плоскостью
плоскостью 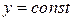 ;
;
частная производная 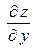 численно равна тангенсу угла наклона b касательной к сечению поверхности
численно равна тангенсу угла наклона b касательной к сечению поверхности 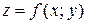 плоскостью
плоскостью 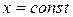 .
.
Пример 2.1. Для данной функции требуется найти частные производные 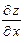 и
и 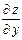 . Найти значения частных производных в точке
. Найти значения частных производных в точке 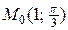 :
:
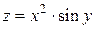 .
.
Решение. Находим частные производные в общем виде:
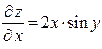 ,
, 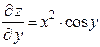 .
.
Находим значения частных производных в точке 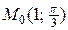 :
:
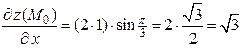 ,
, 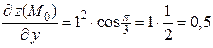 .
.
,
Пример 2.2. Найти частные производные 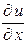 ,
, 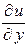 ,
, 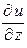 ,
, 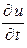 для следующей функции:
для следующей функции:
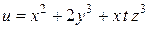 .
.
Решение.
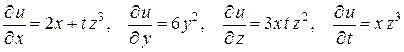 .
.
,
Дата добавления: 2017-09-19; просмотров: 1046;
