Задания для самостоятельного решения
I уровень
1.1. Определите параметры параболы и построить ее:
1) y2 = 2x; 2) y2 = –3x;
3) x2 = 6y; 4) x2 = –y.
1.2. Напишите уравнение параболы с вершиной в начале координат, если известно, что:
1) парабола расположена в левой полуплоскости симметрично относительно оси Ox и p = 4;
2) парабола расположена симметрично относительно оси Oy и проходит через точку M(4; –2).
3) директриса задана уравнением 3y + 4 = 0.
1.3. Составьте уравнение кривой, все точки которой равноудалены от точки (2; 0) и прямой x = –2.
II уровень
2.1. Определить тип и параметры кривой:
1) x2 – 8x + 2y + 18 = 0; 2) x = 2y2 – 12y + 14.
Сделать чертеж.
2.2. Составьте уравнение параболы с вершиной в начале координат, фокус которой находится в точке пересечения прямой 3x – 2y + 5 = 0 с осью ординат.
2.3. Составьте уравнение параболы с вершиной в точке V(3, –2) и фокусом F(3; 0).
2.4. Составьте уравнение параболы с вершиной в точке (–1; 1) и уравнением директрисы y – 1 = 0.
2.5. Составьте уравнение параболы с фокусом 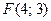 и директрисой
и директрисой 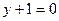 .
.
III уровень
3.1. Составьте уравнение параболы, проходящей через точки (–1; 1), (1; 3) и (31, 9).
3.2. Найдите расстояние от левого фокуса эллипса 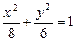 до прямой, проходящей через точки его пересечения с параболой y2 = 12x.
до прямой, проходящей через точки его пересечения с параболой y2 = 12x.
3.3. Составьте полярное уравнение параболы, приняв ее вершину за полюс, а ее ось – за полярную ось.
3.4. Докажите, что множество точек, равноудаленных от точки 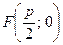 и прямой
и прямой 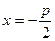 , есть парабола
, есть парабола 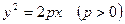 .
.
3.5. Составьте параметрические уравнения параболы 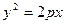 , принимая в качестве параметра ординату
, принимая в качестве параметра ординату 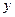 .
.
3.6. Определите уравнение кривой в прямоугольных координатах и постройте ее, если она задана параметрически с помощью уравнений 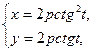
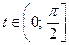 .
.
Дата добавления: 2017-09-19; просмотров: 645;
