Задания для самостоятельного решения
I уровень
1.1. Составьте каноническое уравнение окружности с центром в точке (–4, 7) и радиусом R = 7. Определите, лежат ли на этой окружности точки А(1, –2) и В(–4, 0).
1.2. Найдите центр и радиус окружности:
1) x2 + y2 + 2x = 0; 2) x2 + y2 – 4y = 0.
1.3. Для эллипса 4x2 + 9y2 = 36 найдите:
1) его центр; 2) полуоси; 3) фокусы;
4) эксцентриситет; 5) уравнения директрис.
Сделайте чертеж.
II уровень
2.1. Постройте окружность x2 + y2 – 5y = 0 и прямую 2x – y = 0. Найдите их точки пересечения.
2.2. Дана точка А(4, –2). Составьте уравнение окружности, диаметром которой служит отрезок ОА, и найдите точки пересечения этой окружности с координатными осями.
2.3. Напишите уравнения диаметров окружности x2 + y2 + 6x + + 8y = 0, параллельных координатным осям.
2.4. Составьте уравнение эллипса, зная его фокус F1(2, 0), соответствующую ему директрису x = 8 и ε = 1/2.
2.5. Приведите уравнение к каноническому виду и определите геометрическое множество точек, которое оно задает:
1) x2 + 4y2 – 2x + 16y + 13 = 0;
2) x2 + 4y2 + 2x + 16y + 17 = 0;
3) x2 + 4y2 – 2x + 16y + 21 = 0;
4)
5)
Сделайте чертеж, если это возможно.
2.6. Эллипс касается оси абсцисс в точке А(3, 0) и оси ординат в точке В(0, –2). Составьте уравнение эллипса, если его оси симметрии параллельны координатным осям.
2.7. Эллипс, симметричный относительно координатных осей, проходит через точки M( 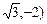 и
и 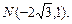 Составьте его уравнение.
Составьте его уравнение.
III уровень
3.1. Докажите, что для эллипса 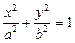
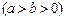 выполняется условие
выполняется условие 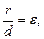 где r – фокальный радиус любой точки эллипса, d – ее расстояние до соответствующей директрисы.
где r – фокальный радиус любой точки эллипса, d – ее расстояние до соответствующей директрисы.
3.2. Эллипс, главные оси которого совпадают с координатными осями, проходит через точки 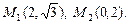 Составьте его уравнение, найдите фокальные радиусы точки М1 и расстояния от этой точки до директрис.
Составьте его уравнение, найдите фокальные радиусы точки М1 и расстояния от этой точки до директрис.
3.3. На эллипсе 9x2 + 25y2 = 225 найдите точку, расстояние от которой до одного из фокусов в 4 раза больше расстояния до второго фокуса.
3.4. Выведите каноническое уравнение эллипса, используя то, что сумма расстояний от любой из его точек до фокусов есть величина постоянная, равная большой оси, то есть 2а (считать, что фокусы расположены на оси абсцисс симметрично относительно начала координат, и междуфокусное расстояние равно 2с, с < а).
Гипербола
Гиперболой называется геометрическое место точек плоскости, координаты которых удовлетворяют уравнению
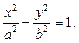 (25)
(25)
где 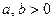 .
.
Параметры гиперболы:
Точки F1(–c, 0), F2(c, 0), где 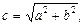 называются фокусами гиперболы, при этом величина 2с (с > a > 0) определяет междуфокусное расстояние. Точки А1(–а, 0), А2(а, 0) называются вершинами гиперболы, при этом А1А2 = 2а образует действительную ось гиперболы, а В1В2 = 2b – мнимую ось (В1(0, –b), B2(0, b)), О – центр гиперболы.
называются фокусами гиперболы, при этом величина 2с (с > a > 0) определяет междуфокусное расстояние. Точки А1(–а, 0), А2(а, 0) называются вершинами гиперболы, при этом А1А2 = 2а образует действительную ось гиперболы, а В1В2 = 2b – мнимую ось (В1(0, –b), B2(0, b)), О – центр гиперболы.
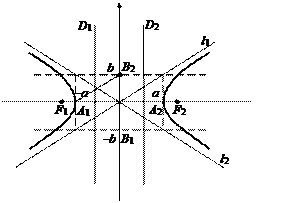 |
Рис. 19
Величина 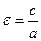 называется эксцентриситетом гиперболы, она характеризует меру «сжатости» гиперболы;
называется эксцентриситетом гиперболы, она характеризует меру «сжатости» гиперболы;
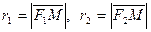 – фокальные радиусы гиперболы (точка М принадлежит гиперболе), причем r1 = a + εx, r2 = –a + εx для точек правой ветви гиперболы, r1 = – (a + εx), r2 = – (–a + εx) – для точек левой ветви;
– фокальные радиусы гиперболы (точка М принадлежит гиперболе), причем r1 = a + εx, r2 = –a + εx для точек правой ветви гиперболы, r1 = – (a + εx), r2 = – (–a + εx) – для точек левой ветви;
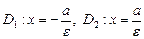 – директрисы гиперболы;
– директрисы гиперболы;
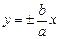 – уравнения асимптот.
– уравнения асимптот.
Для гиперболы справедливо: ε > 1, директрисы не пересекают границу и внутреннюю область гиперболы, а также обладают свойством 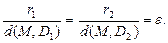
Говорят, что уравнение
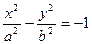 (26)
(26)
задает уравнение гиперболы, сопряженной данной (рис. 20). Его можно записать также в виде
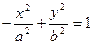 .
.
В таком случае ось 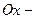 мнимая, фокусы лежат на оси
мнимая, фокусы лежат на оси 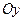 . Все остальные параметры определяются аналогично как для гиперболы (25).
. Все остальные параметры определяются аналогично как для гиперболы (25).
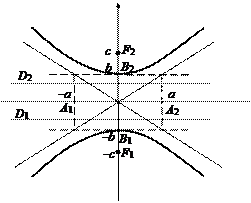 |
Рис. 20
Точки гиперболы обладают важным характеристическим свойством: абсолютное значение разности расстояний от каждой из них до фокусов есть величина постоянная, равная 2a (рис. 19).
Для параметрического задания гиперболы в качестве параметра t может быть взята величина угла между радиус-вектором точки, лежащей на гиперболе, и положительным направлением оси Ox:
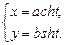
Пример 1. Привести уравнение гиперболы
9x2 – 16y2 = 144
к каноническому виду, найти еепараметры, изобразить гиперболу.
Решение. Разделим левую и правую части заданного уравнения на 144: 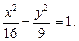 Из последнего уравнения непосредственно следует: a = 4, b = 3, c = 5, O(0, 0) – центр гиперболы. Фокусы находятся в точках F1(–5, 0) и F2(5, 0), эксцентриситет ε = 5/4, директрисы D1 и D2 описываются уравнениями D1: x = –16/5, D2: x = 16/5, асимптоты l1 и l2 имеют уравнения
Из последнего уравнения непосредственно следует: a = 4, b = 3, c = 5, O(0, 0) – центр гиперболы. Фокусы находятся в точках F1(–5, 0) и F2(5, 0), эксцентриситет ε = 5/4, директрисы D1 и D2 описываются уравнениями D1: x = –16/5, D2: x = 16/5, асимптоты l1 и l2 имеют уравнения 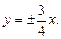
Сделаем чертеж. Для этого по осям Ox и Oy симметрично относительно точки (0, 0) отложим отрезки А1А2 = 2а = 8 и В1В2 = 2b = 6 соответственно. Через полученные точки А1(–4, 0), А2(4, 0), В1(0, –3), В2(0, 3) проведем прямые, параллельные координатным осям. В результате получим прямоугольник (рис. 21), диагонали которого лежат на асимптотах гиперболы. Строим гиперболу
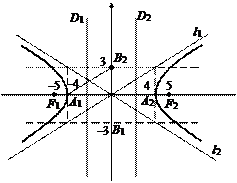 |
Рис. 21
Для нахождения угла φ между асимптотами гиперболы воспользуемся формулой
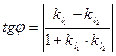 .
.
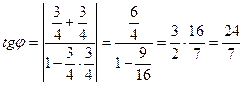 ,
,
откуда получаем 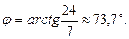
Пример 2. Определить тип, параметры и расположение на плоскости кривой, уравнение которой
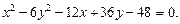
Решение. С помощью метода выделения полных квадратов упростим правую часть данного уравнения:
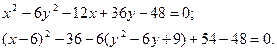
Получаем уравнение
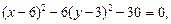
которое делением на 30 приводится к виду
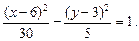
Это уравнение гиперболы, центр которой лежит в точке 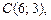 действительная полуось –
действительная полуось – 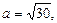 мнимая полуось –
мнимая полуось – 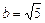 (рис. 22).
(рис. 22).
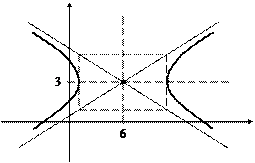 |
Рис. 22
Пример 3. Составить уравнение гиперболы, сопряженной относительно гиперболы 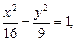 определить ее параметры и сделать чертеж.
определить ее параметры и сделать чертеж.
Решение.Уравнение гиперболы, сопряженной данной, –
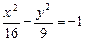 или
или 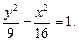
Действительная полуось b = 3, мнимая – а = 4, половина междуфокусного расстояния 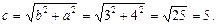 Вершинами гиперболы служат точки B1(0, –3) и В2(0, 3); ее фокусы находятся в точках F1(0, –5) и F2(0, 5); эксцентриситет ε = с/b = 5/3; директрисы D1 и D2 задаются уравнениями D1: y = –9/5, D2: y = 9/5; уравнения
Вершинами гиперболы служат точки B1(0, –3) и В2(0, 3); ее фокусы находятся в точках F1(0, –5) и F2(0, 5); эксцентриситет ε = с/b = 5/3; директрисы D1 и D2 задаются уравнениями D1: y = –9/5, D2: y = 9/5; уравнения 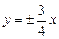 являются уравнениями асимптот (рис. 23).
являются уравнениями асимптот (рис. 23).
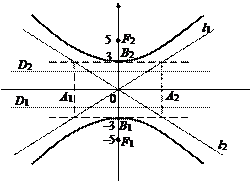 |
Рис. 23
Заметим, что для сопряженных гипербол общими элементами являются вспомогательный «прямоугольник» и асимптоты.
Пример 4. Написать уравнение гиперболы с полуосями a и b (a > 0, b > 0), если известно, что ее главные оси параллельны координатным осям. Определить основные параметры гиперболы.
Решение. Искомое уравнение можно рассматривать как уравнение гиперболы 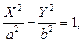 которое получается в результате параллельного переноса старой системы координат на вектор
которое получается в результате параллельного переноса старой системы координат на вектор 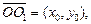 где (x0, y0) – центр гиперболы в «старой» системе координат. Тогда, используя соотношения между координатами произвольной точки М плоскости в заданной и преобразованной системах
где (x0, y0) – центр гиперболы в «старой» системе координат. Тогда, используя соотношения между координатами произвольной точки М плоскости в заданной и преобразованной системах
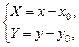
получим уравнение гиперболы
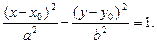
Определим параметры. Центр гиперболы определяет точка O¢(x0; y0), а значит, действительная ось задается уравнением x = x0,а мнимая – уравнением y = y0. Ее вершинами являются точки 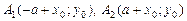 , а асимптотами являются прямые
, а асимптотами являются прямые 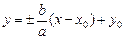 . Половина междуфокусного расстояния
. Половина междуфокусного расстояния 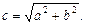 Тогда фокусы гиперболы находятся в точках
Тогда фокусы гиперболы находятся в точках 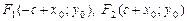 , эксцентриситет
, эксцентриситет
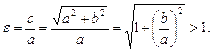
Директрисы D1 и D2 задаются уравнениями
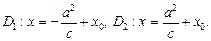
Пример 5.Написать уравнение гиперболы, имеющей вершины в фокусах эллипса 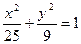 , а фокусы – в вершинах этого эллипса.
, а фокусы – в вершинах этого эллипса.
Решение.Уравнение 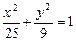 означает, что фокусами эллипса являются точки
означает, что фокусами эллипса являются точки 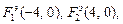 а вершины, лежащие на главной оси, находятся в точках
а вершины, лежащие на главной оси, находятся в точках 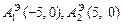 (так как
(так как 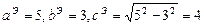 ).
).
Тогда для искомой гиперболы известно, что
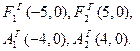
Значит, основные параметры гиперболы есть:
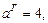
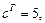
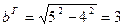 .
.
Используя данную информацию, приходим к уравнению гиперболы
Дата добавления: 2017-09-19; просмотров: 996;
