Задания для самостоятельного решения

I уровень

1.1. Найдите полярные координаты точек A(1, 1), B 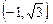C(–2, 2), D(0, 1), E(–3, 0), F(2, 0), G(0, –1), H(1, )

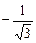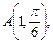
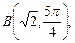
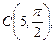
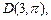
1.2. Зная полярные координаты точек 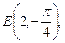найдите их прямоугольные координаты.

1.3. Уравнение линии на плоскости задано в прямоугольных координатах. Найдите их соответствующее уравнение в полярных координатах (полюс совпадает с началом прямоугольной системы координат, полярная ось – с осью абсцисс):

1) ρ = 2; 2) 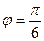; 3) ρ = 2sinφ.

1.4. Найдите уравнение линии в прямоугольной системе координат, если известны параметрические уравнения (исключить параметр):

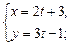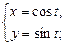1) 2) 3)

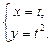
II уровень

2.1. Найдите полярные координаты точек, симметричных им относительно полярной оси

.

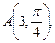
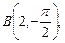
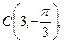
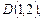
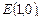
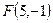2.2. Даны полярные координаты точек 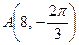и 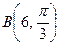. Вычислите полярные координаты середины отрезка АВ.

2.3. Определите, какую кривую на плоскости образуют точки, для которых расстояние от точки А(4, 0) вдвое больше расстояния от точки В(1, 0).

2.4. Найдите полярные уравнения фигур, если известны их уравнения в прямоугольной системе координат xOy:

1) 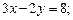2)

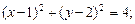
3)

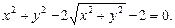
III уровень

3.1. Найдите уравнение кривой, состоящей из тех точек плоскости, разность расстояний от которых до точек F₁(–2, –2) и F₂(2, 2) равна 4.

3.2. Составьте параметрические уравнения окружности x² + y² – 2x = 0, приняв за параметр угол между осью Ox и прямой, проходящей через центр окружности.

3.3. Опишите с помощью уравнения в полярных координатах множество точек, лежащих на прямой, перпендикулярной полярной оси и проходящей через точку А(5, 0).

3.4. Уравнения кривых заданы в полярных координатах. Найдите их уравнения в соответствующих прямоугольных координатах:

1) ρ² = sinφ; 2) ρ = cosφ + sinφ;

3) ρ²cosφ sinφ = 1; 4) ρ² – 2 ρcosφ – 3 = 0.