Задания для самостоятельного решения
I уровень
1.1. Даны векторы 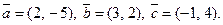
Найдите координаты вектора:
1) 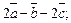 2)
2) 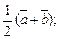
3) 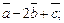 4)
4) 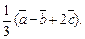
1.2. Даны векторы 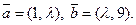 Определите, при каком значении
Определите, при каком значении 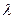 векторы
векторы 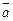 и
и 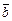 коллинеарны.
коллинеарны.
1.3. Вектор 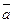 образует с ортом
образует с ортом 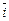 угол α. Вычислите координаты вектора
угол α. Вычислите координаты вектора 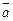 на плоскости, если:
на плоскости, если:
1) 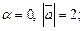 2)
2) 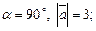
3) 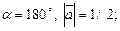 4)
4) 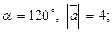
5) 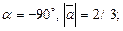 6)
6) 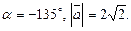
1.4. Заданы векторы 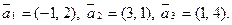 Вычислите:
Вычислите:
1) 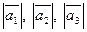 ;
;
2) орты векторов 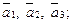
3) 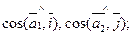
4) координаты вектора 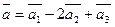 .
.
1.5. Вычислите скалярное произведение векторов, заданных своими координатами:
1) 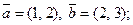 2)
2) 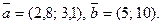
1.6. Найдите угол между векторами:
1) 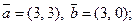 2)
2) 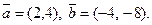
1.7. Вычислите работу, производимую силой 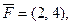 при перемещении ее точки приложения из начала в конец вектора
при перемещении ее точки приложения из начала в конец вектора 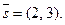
II уровень
2.1. Известно, что A(2, –7), B(4, 1). Найдите:
1) координаты вектора 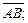 2)
2) 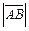 ;
;
3) орт вектора 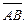
2.2. Даны векторы 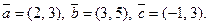 Определите, при каком значении коэффициента k векторы коллинеарны:
Определите, при каком значении коэффициента k векторы коллинеарны:
1) 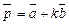 и
и 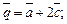
2) 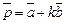 и
и 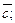
3) 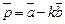 и
и 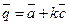 .
.
2.3. Известно, что вектор 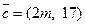 является суммой векторов
является суммой векторов 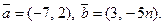 Найдите m и n.
Найдите m и n.
2.4. Отрезок с концами в точках А(3, –2) и В(6, 4) разделен на три равные части. Найдите координаты точек деления.
2.5. Вычислите скалярное произведение векторов 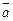 и
и 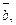 если:
если:
1) 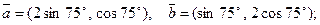
2) 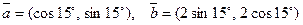 .
.
III уровень
3.1. Сила 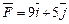 разложена по двум перпендикулярным направлениям, одно из которых задано вектором
разложена по двум перпендикулярным направлениям, одно из которых задано вектором 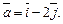 Найдите направляющую силы в направлении этого вектора.
Найдите направляющую силы в направлении этого вектора.
3.2. Подберите ненулевые числа α, β, γ так, чтобы 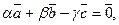 где
где 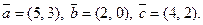
3.3. Даны три вершины А(3, –4), В(–5, 3) и С(1, 2) параллелограмма ABCD. Найдите его четвертую вершину D.
3.4. Даны вершины треугольника А(3, –1), В(4, 2) и С(–4, 0). Найдите длину медианы, проведенной из вершины А.
3.5. Даны вершины А(1, –1), В(2, 1), С(–5, 2) треугольника АВС. Вычислите длину биссектрисы его внутреннего угла при вершине А.
3.6. Треугольник АВС задан координатами своих вершин: А(3, –2), В(3, 1), С(4, 0). Вычислите расстояние от начала координат до точки пересечения медиан этого треугольника.
3.7. В вершинах треугольника А(1, –1), В(0, 4) и С(2, –1) сосредоточены массы соответственно 1, 2, 3. Найдите координаты центра масс этой системы. (Указание: для пары масс m1 и m2, сосредоточенных в точках А и В, центр находится в точке, делящей отрезок АВ в отношении 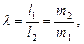 где l1 и l2 – расстояния от точек с соответствующими массами до их центра).
где l1 и l2 – расстояния от точек с соответствующими массами до их центра).
3.8. Даны векторы 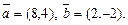 Найдите вектор
Найдите вектор 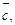 лежащий с векторами
лежащий с векторами 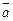 и
и 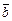 в одной плоскости, перпендикулярный вектору
в одной плоскости, перпендикулярный вектору 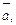 равный ему по длине и образующий с вектором
равный ему по длине и образующий с вектором 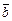 тупой угол.
тупой угол.
3.9. Представьте ненулевой вектор 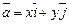 в виде линейной комбинации векторов
в виде линейной комбинации векторов 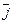 и
и 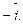
Дата добавления: 2017-09-19; просмотров: 444;
