Задания для самостоятельного решения

I уровень

1.1. В шаре на расстоянии 9см от центра проведено сечение, площадь которого 144p см². Найдите радиус шара.

1.2. Два равных шара с радиусом R = 17 см, взаимно пересекаясь, образуют двояковыпуклую линзу. Найдите ее диаметр, если расстояние между центрами шаров равно R.

1.3. Найдите высоту шарового сегмента, если радиус его основания 15см, а радиус шара 25 см.

1.4. Шар, радиус которого 15 см, пересечен плоскостью на расстоянии 9 см от центра. Найдите площадь сферической части шарового сегмента.

1.5. Найдите площадь сферы, диаметр которой равен диагонали куба с ребром равным 2 см.

1.6. Определите, во сколько раз объем Земли больше объема Луны. (Диаметр Земли следует принять за 13тыс. км, диаметр Луны – 3,5тыс. км.)

1.7. Объем стенок полого шара равен 876p см³, а толщина стенок – 3 см. Найдите радиусы наружной и внутренней поверхностей шара.

1.8. Найдите объем шарового сектора, если радиус шара 10 см, а радиус основания соответствующего шарового сегмента 6 см.

1.9. Объем одного шара в 8 раз больше объема другого шара. Определите, во сколько раз площадь поверхности первого шара больше площади поверхности второго.

II уровень

2.1. Стороны треугольника, равные 5 см, 5 см и 6 см, касаются шара, радиус которого 2,5 см. Найдите расстояние от центра шара до плоскости треугольника.

2.2. На поверхности шара даны три точки. Расстояния между ними 7 см. Радиус шара равен 7 см. Найдите расстояние от центра шара до плоскости, проходящей через данные три точки.

2.3. Радиусы оснований шарового слоя равны 63 см и 39 см, его высота36 см. Найдите радиус шара.

2.4. Дан шар радиуса 12 см. Через одну точку его поверхности проведены две плоскости: первая – касательна к шару, вторая – под углом 60° к радиусу, проведенному в точку касания. Найдите площадь сечения.

2.5. Определите, какую площадь имеет часть поверхности шара, которая видна наблюдателю, находящемуся на расстоянии 10 м от него, если радиус воздушного шара равен 15 м.

2.6. Шар пересечен двумя плоскостями, проходящими через оду точку поверхности шара и образующими угол 60°. Радиус шара равен 4 см. Найдите площади поверхностей отсекаемых сегментов, если окружности их оснований имеют равные радиусы.

2.7. Шар касается граней двугранного угла в 120°. Расстояние от центра шара до ребра угла равно 10 см. Найдите площадь поверхности шара.

2.8. Из шара вырезали шаровой слой, толщина которого 9 см, площади оснований 400p см² и 49p см². Найдите объемы оставшихся шаровых сегментов.

2.9. Диаметр шара разделен на четыре равные части и через точки деления проведены секущие плоскости перпендикулярные диаметру. Найдите объемы полученных частей шара, если его радиус равен R.

2.10. В шаре радиуса R просверлено цилиндрическое отверстие. Ось цилиндра проходит через центр шара, диаметр отверстия равен радиусу шара. Найдите объем оставшейся части шара.

III уровень

3.1. Плоскости двух сечений шара взаимно перпендикулярны. Одна из этих плоскостей проходит через центр, другая удалена от него на 12. Общая хорда сечений равна 18. Найдите сумму площадей этих сечений.

3.2. Радиус шара 15 м. Вне шара дана точка А на расстоянии 10м от его поверхности. Найдите радиус такой окружности на поверхности шара, все точки которой отстоят от А на 20 м.

3.3. Из точки, взятой на поверхности шара, проведены три равные хорды, угол между каждой парой которых равен a. Найдите длину хорды, если радиус шара R.

3.4. Два шара внутренне касаются в точке А, АВ – диаметр большего из шаров, ВС – касательная к меньшему из них. Найдите радиусы шаров, если ВС = 20 см, а разность площадей поверхностей шаров равна 700p см².

3.5. Вычислите объем шара, радиус которого равняется ребру октаэдра, имеющего поверхность площадью 10 .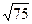

3.6. Круговой сектор с углом 60° и радиусом R вращается около одного из боковых радиусов. Найдите объем полученного тела вращения.