Задания для самостоятельного решения
I уровень
1.1. Боковое ребро правильной четырехугольной пирамиды равно диагонали основания, длина которой 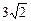 см. Найдите высоту пирамиды и сторону ее основания.
см. Найдите высоту пирамиды и сторону ее основания.
1.2. Основанием пирамиды является треугольник со сторонами 6 см, 8 см и 10 см. Боковые грани наклонены к плоскости основания под углом 60º. Найдите высоту пирамиды.
1.3. Найдите площадь полной поверхности правильной шестиугольной пирамиды, зная, что апофема равна 10 см, а радиус окружности, описанной около основания, равен 6см.
1.4. Найдите высоту правильной четырехугольной пирамиды, сторона которой 6 см, если ее объем равен объему куба со стороной 4 см.
1.5. Боковые ребра треугольной пирамиды взаимно перпендикулярны и равны b. Найдите объем пирамиды.
1.6. Стороны оснований правильной усеченной четырехугольной пирамиды 8 см и 4 см. Боковое ребро 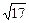 см. Найдите высоту пирамиды.
см. Найдите высоту пирамиды.
1.7. Боковые ребра правильной усеченной шестиугольной пирамиды наклонены к плоскости нижнего основания под углом 45º. Стороны оснований равны 10 см и 5 см. Найдите длину бокового ребра и высоту пирамиды.
1.8. Боковая грань правильной семиугольной усеченной пирамиды – равнобедренная трапеция, средняя линия которой 13 см, а высота 8 см. Вычислите площадь боковой поверхности пирамиды.
1.9. Площадь полной поверхности правильной треугольной усеченной пирамиды равна 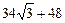 см2. Стороны оснований 10 см и 6 см. Найдите тангенс угла между боковым ребром и стороной нижнего основания.
см2. Стороны оснований 10 см и 6 см. Найдите тангенс угла между боковым ребром и стороной нижнего основания.
1.10. В правильной усеченной четырехугольной пирамиде стороны оснований равны 5 см и 17 см, боковые грани наклонены к плоскости основания под углом 45º. Вычислите объем пирамиды.
II уровень
2.1. По стороне основания, равной 5 см, и высоте, равной 12 см, Найдите апофему и боковое ребро правильной шестиугольной пирамиды.
2.2. Найдите расстояние между центрами окружностей вписанных в смежные боковые грани тетраэдра. Радиус окружности равен 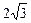 дм.
дм.
2.3. Основание пирамиды – ромб со стороной 6см и углом 45º, все двугранные углы при сторонах основания пирамиды равны 30º. Вычислите площадь полной поверхности пирамиды.
2.4. В правильной треугольной пирамиде боковое ребро равно 8 см, а плоский угол при вершине – 30º. Найдите площадь полной поверхности пирамиды.
2.5. Одно из самых грандиозных сооружений древности – пирамида Хеопса – имеет форму правильной четырехугольной пирамиды с высотой » 150 м и боковым ребром » 220 м. Найдите объем этой пирамиды.
2.6. Определите объем правильной треугольной пирамиды, если боковая грань наклонена к плоскости основания под углом 60º и удалена от противоположной вершины на расстояние, равное 3 см.
2.7. В правильной четырехугольной усеченной пирамиде стороны оснований равны 15 дм и 5 дм. Площадь диагонального сечения равна 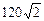 дм2. Найдите площадь полной поверхности пирамиды.
дм2. Найдите площадь полной поверхности пирамиды.
2.8. Основания усеченной пирамиды – равнобедренные треугольники, их равные стороны – 8 см и 4 см, углы при вершинах треугольников равны по 120º. Ребро, проходящее через вершины данных углов, перпендикулярно плоскости оснований и равно 3 см. Вычислите площадь боковой поверхности пирамиды.
2.9. Правильная четырехугольная пирамида, сторона основания которой 1500 см и высота 2000 см, пересечена плоскостью параллельной основанию. Найдите объем усеченной пирамиды, если ее высота 1400 см.
2.10. В правильной усеченной треугольной пирамиде стороны оснований равны 7 см и 3 см, а апофема – 5 см. Найдите объем пирамиды.
III уровень
3.1. Основанием пирамиды является равносторонний треугольник. Одна из боковых граней пирамиды перпендикулярна плоскости основания, две другие образуют с плоскостью основания угол a. Найдите косинус угла между этими гранями.
3.2. Все диагональные сечения правильной шестиугольной пирамиды SABCDEF равновелики. Найдите угол между плоскостью основания и плоскостью сечения SAC.
3.3. Точка М – середина ребра SB пирамиды SABC, основанием которой является правильный треугольник ABC, а боковое ребро SC перпендикулярно плоскости ABC и SC = 2AB. Найдите расстояние от точки М до прямой AC, если АВ = а.
3.4. Основанием пирамиды служит ромб со стороной а и острым углом a. Две боковые грани перпендикулярны основанию, а две другие наклонены к нему под углом j. Найдите площадь боковой поверхности пирамиды.
3.5. Основанием пирамиды является равнобокая трапеция, острый угол которой a, а площадь Q. Каждая боковая грань образует с основанием угол b. Найдите объем пирамиды.
3.16. Основание усеченной пирамиды – прямоугольник со сторонами 6 см и 8 см. Одно из боковых ребер перпендикулярно плоскости основания и равно 7 см. Вершина верхнего основания проектируется в точку пересечения диагоналей нижнего основания. Найдите длины остальных боковых ребер и угол наклона большего бокового ребра к плоскости основания.
3.7. Основания усеченной пирамиды – квадраты со сторонами 8 см и 4 см. Одна из боковых граней перпендикулярна плоскости основания и является равнобедренной трапецией. Противолежащая ей грань образует с плоскостью основания угол 60º. Найдите площади боковых граней пирамиды.
3.8. Стороны оснований и высота правильной четырехугольной усеченной пирамиды относятся, как 7 : 4 : 2, площадь боковой поверхности равна 110 дм2. Вычислите площадь полной поверхности пирамиды.
3.9. Найдите объем правильной треугольной усеченной пирамиды, у которой стороны оснований равны 3 м и 2 м, а площадь боковой поверхности равна сумме площадей оснований.
3.10. Стороны оснований правильной четырехугольной усеченной пирамиды равны 2 см и 1 см, высота – 3 см. Через точку пересечения диагоналей пирамиды, параллельно основаниям пирамиды, приведена плоскость, делящая пирамиду на две части. Найдите объем каждой из полученных частей.
Цилиндр
Цилиндрической поверхностью называется поверхность, образованная всеми прямыми, проходящими через каждую точку данной кривой параллельно данной прямой (рис. 25).
Данная кривая называется направляющей, а прямые – образующими цилиндрической поверхности.
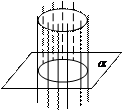
Прямой круговой цилиндрической поверхностью называется поверхность, образованная всеми прямыми, проходящими через каждую точку данной окружности перпендикулярно плоскости этой окружности. В дальнейшем эту поверхность будем кратко называть цилиндрической (рис. 26).
Цилиндром (прямым круговым цилиндром) называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые перпендикулярны образующим поверхности (рис. 27).
Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг оси, содержащей одну из сторон прямоугольника.
Два круга, ограничивающие цилиндр, называются его основаниями. Прямая, проходящая через центры данных кругов, называется осью цилиндра. Отрезки, образующие цилиндрическую поверхность, называются образующими цилиндра. Высотой цилиндра называется расстояние между его основаниями. Осевым сечением называется сечение, проходящее через ось цилиндра. Разверткой боковой поверхности цилиндра называется прямоугольник со сторонами равными длине окружности основания и длине образующей цилиндра.
 | |||||||
 | |||||||
 | |||||||
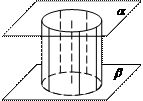 | |||||||
Рис. 25 Рис. 26 Рис. 27
Для цилиндра верны формулы:
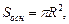
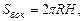
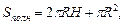 (5)
(5)
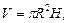 (6)
(6)
где R – радиус основания;
H – высота;
Sосн – площадь основания;
Sбок – площадь боковой поверхности;
Sполн – площадь полной поверхности;
V – объем цилиндра.
Пример 1. Найти радиус основания цилиндра, если его высота равна 8 см, а диагональ осевого сечения составляет угол в 45º с плоскостью основания.
Решение. Сделаем рисунок (рис. 28).
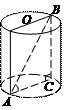 |
Рис. 28
Осевое сечение цилиндра – это прямоугольник, одна сторона которого образующая (высота) цилиндра, вторая сторона – диаметр основания цилиндра. Рассмотрим треугольник АВС, у которого катетами являются диаметр основания АС и высота ВС, а гипотенузой – диагональ сечения АВ. Так как 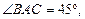 то
то 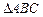 – равнобедренный и АС = ВС = 8 см. АС – диаметр, значит, радиус
– равнобедренный и АС = ВС = 8 см. АС – диаметр, значит, радиус 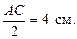
Ответ: 4 см.
Пример 2. Цилиндр пересечен плоскостью параллельной оси. Найти площадь сечения, если радиус основания и высота цилиндра соответственно 5 см и 10 см, а расстояние от оси цилиндра до плоскости сечения 3 см.
Решение. Сделаем рисунок (рис. 29).
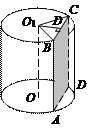
Рис. 29
Сечением цилиндра является прямоугольник, одна из сторон которого – хорда окружности основания (ВС), вторая – образующая цилиндра (ВА). Образующая равна высоте, значит ВА = 10 см. Необходимо найти хорду ВС. Расстояние от оси ОО1 до плоскости сечения – это перпендикуляр опущенный из точки О1 на хорду ВС. Проведя радиусы О1С и О1В, получим равнобедренный треугольник 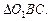 Высота O1D является его медианой, значит BD = DC. Из
Высота O1D является его медианой, значит BD = DC. Из 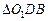 найдем BD:
найдем BD:
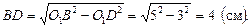
Тогда BC = 2BD = 8 см. Площадь сечения:
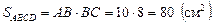
Ответ: 80 см2.
Пример 3. Диагональ сечения цилиндра, параллельного его оси, равна d и образует угол a с образующей цилиндра. Найти площадь полной поверхности цилиндра, если секущая плоскость отсекает от окружности основания 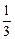 часть ее.
часть ее.
Решение. Сделаем рисунок (рис. 30).
 | |||
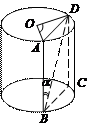 | |||
Рис. 30
Площадь полной поверхности цилиндра вычисляется по формуле (5).
Чтобы найти высоту Н (образующую), рассмотрим 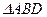 . В нем
. В нем 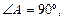
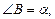
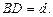 Тогда
Тогда
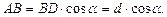
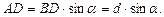
Для нахождения радиуса рассмотрим равнобедренный 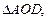 в котором OA = OD = R. Так как по условию сечение отсекает от окружности основания
в котором OA = OD = R. Так как по условию сечение отсекает от окружности основания 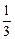 часть, значит
часть, значит 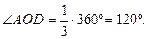 По теореме косинусов найдем радиус:
По теореме косинусов найдем радиус:
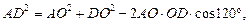
т.е. 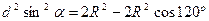 .
.
Тогда 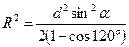 , откуда получаем
, откуда получаем
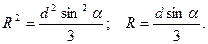
Вычисляем
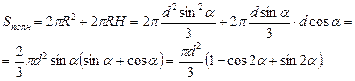
Ответ: 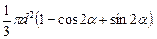
Пример 4.Диагонали развертки боковой поверхности цилиндра образуют острый угол равный a. Высота цилиндра равна h. Найти объем цилиндра.
Решение. Сделаем рисунок (рис. 31).
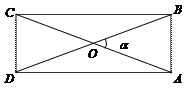
Рис. 31
Чтобы найти объем, необходимо знать радиус основания цилиндра. Рассмотрим развертку боковой поверхности цилиндра – прямоугольник ABCD: AD = h, BC = 2pR,где R – неизвестный радиус основания. Точка О – середина диагоналей. Из точки О опустим перпендикуляр OD,
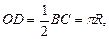 с другой стороны
с другой стороны
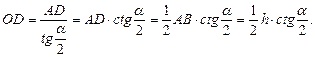
Приравнивая выражения для нахождения OD, находим R:
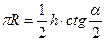 , т.е.
, т.е. 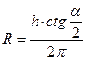 .
.
Вычисляем объем цилиндра по формуле (6):
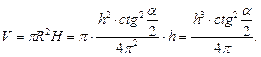
Ответ: 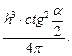
Дата добавления: 2017-09-19; просмотров: 2473;
