Законы распределения случайных величин
Экономические показатели, как правило, являются случайными величинами.
Случайной величиной называется величина, которая в результате опыта (испытания) может принять одно и только одно возможное значение, заранее неизвестное и зависящее от случайных причин.
Случайные величины бывают дискретными и непрерывными.
Дискретной называют случайную величину, принимающую отдельные, изолированные друг от друга возможные значения, которые можно пронумеровать. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Например, количество реализованных акций за некоторый период времени есть дискретная случайная величина. Ее возможные значения: 0,1,2,...
Непрерывной называют случайную величину, которая может принимать все возможные значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.
Примером непрерывной случайной величина может служить прибыль фирмы за год.
Будем обозначать случайные величины заглавными буквами Х, У, а их возможные значения - строчными буквами х, у.
Случайная величина полностью описывается своим законом распределения.
Законом распределения случайной величины называется соотношение, устанавливающее связь между ее возможными значениями и соответствующими им вероятностями. Закон распределения может быть задан таблично (рядом распределения для дискретной величины), графически и аналитически (функцией распределения или функцией плотности распределения для непрерывной величины).
Рядом распределения дискретной случайной величины X называется таблица, где в первой строке перечислены возможные значения этой величины х1, х2, …, хп, а вторая строка содержит соответствующие им вероятности Р1, P2, ...,Рn.
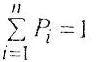При этом
Графическое изображение ряда распределения называют многоугольником (полигоном) распределения.
Случайную величину любого типа (дискретную и непрерывную) можно задать функцией распределения вероятностей.
Функцией распределения случайной величины Х называют функцию F(x), определяющую вероятность того, что величина Х результате опыта примет значение, меньшее х:
F(x) = P(X<x).
Функцию распределения F(x) называют еще интегральной функцией распределения или интегральным законом распределения.
Свойства функции распределений:
1) 0<F(x)<1.
2) Функция F(x) есть неубывающая функция своего аргумента, то есть из соотношения х2 ≥ х1 следует соотношение F(х2) ≥ F(х1).
3) Вероятность попадания случайной величины на заданный участок выражается через функцию распределения F(x) следующим образом:
Р (α<Х <β) = F(β)-F(α).
Таким образом, вероятность попадания случайной величины на заданный участок равна приращению функции распределения на этом участке.
Если величина X непрерывна, то Р(Х=α) = 0.
Тогда Р(α<Х <β)= Р(α≤Х <β) = Р(α<Х ≤β) = Р(α≤Х ≤β)= F(β) - F (α).
4) Для непрерывной случайной величины F(-∞) = 0; F(+∞)= 1.
5) Для дискретной случайной величины F(x) есть разрывная ступенчатая функция, непрерывная слева.
Если функция распределения F(x) всюду непрерывна и имеет производную, то случайная величина называется непрерывной в узком смысле слова (или просто непрерывной).
Если функция F(x) нанекоторых участках непрерывна, а в отдельных точках имеет разрывы, случайная величина называется смешанной.
Пример. Статистика последних 3 лет свидетельствует о том, что месячная прибыль фирмы (тыс. долл.) является случайной величиной, которая описывается функцией распределения, изображенной на рисунке 1.
По виду графика оценить:
1) вероятность того, что прибыль произвольно взятого месяца будет заключена в пределах от 15 до 25 тыс. долл.;
2) вероятность того, что прибыль произвольно взятого месяца будет не менее 20 тыс. долл.;
3) вероятность того, что в произвольно взятом месяце будут убытки.
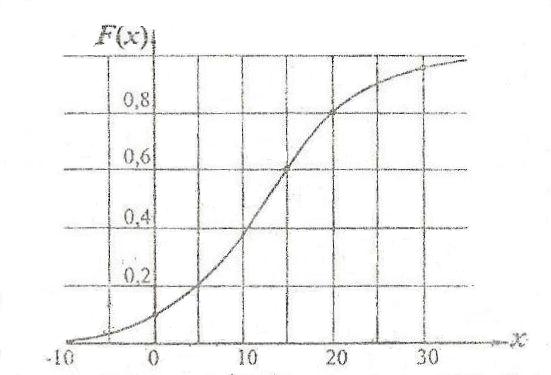
Рис.1 Случайная величина, которая описывается функцией распределения
Решение.
Из графика видно, чтоF(0)=0,1; F(15)=0,6; F(20)=0,8; F(25)=0,9.
Следовательно
1) вероятность того, что прибыль произвольно взятого месяца будет заключена в пределах от 15 до 25 тыс. долл., равна F(25) - F(15)= 0,9 – 0,6 = 0,3
2) вероятность того, чтоприбыль произвольно взятого месяца будет не менее 20 тыс. долл., равна 1- F(20)=1-0,8 = 0,2
3) вероятность того, что в произвольно взятом месяце будут убытки, равна F(0)=0,1
Функцией плотности распределения случайной величины Х называют f(x), являющуюся первой производной функции распределения F(x): f(x) = F’(x)
Плотность распределения существует только для непрерывных случайных величин и имеет следующие основные свойства:
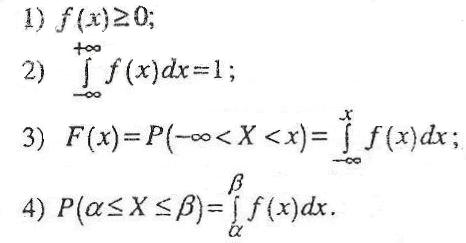
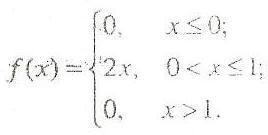
Пример. Функция распределения непрерывной случайной величины Х задана выражением:
Найти: Коэффициент а, плотность распределения f(x); вероятность попадания случайной величины на участок от 0,25 до 0,5.
Решение.
Так как функцияF(x) непрерывна, то при х=1 ах2=1.
Отсюда а = 1.
Плотность распределения случайной величины Х выражается формулой:
Вероятность попадания величины Х на участок можно определить двумя способами:
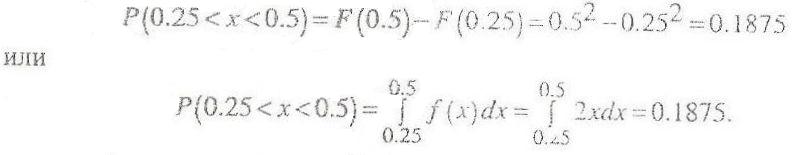
Дата добавления: 2017-09-19; просмотров: 284;