Графический способ изображения статистических данных.
Графическим способом изображения статистических данных называют их условное изображение при помощи точек, линий, плоскостей, геометрических фигур и условных знаков. Графики в статистике применяются для: сравнения одноименных показателей, относящихся к различным объектам; наглядного представления структуры совокупности и ее изменения; характеристики динамики и степени распространения явления; отображения взаимосвязи явлений.
В зависимости от назначения используют различные виды графиков: линейные, столбиковые, ленточные, секторные, фигурные.
Линейные диаграммыобычно применяют для характеристики динамики явлений, их взаимосвязи.
Столбиковые, ленточные диаграммыиспользуются для сравнения значений статистических показателей, характеризующих изучаемые объекты в разные моменты времени (за разные периоды времени).
Секторные диаграммыиспользуются для характеристики структуры совокупности.
Фигурные диаграммы используют при сравнении различных явлений по степени их распространения.
Дискретные вариационные ряды изображают в виде полигона (многоугольника) распределения.
Полигон распределения строится в прямоугольной системе координат. На оси абсцисс откладываются варианты, а на оси ординат наносится шкала частот. На оси абсцисс отмечаются точки, соответствующие величинам вариант, и из них восстанавливаются перпендикуляры, длины которых соответствуют частотам конкретных вариант. В результате соединения концов перпендикуляров отрезками прямой, получают полигон распределения. При этом первую точку следует соединить с точкой на оси абсцисс, соответствующей предшествующей варианте, частота которой равна нулю. Последнюю точку следует также соединить с точкой на оси абсцисс, соответствующей варианте, следующей за последней (частота ее также равна нулю). Таким образом получается многоугольник, изображающий распределение признака (рис. 1.1).
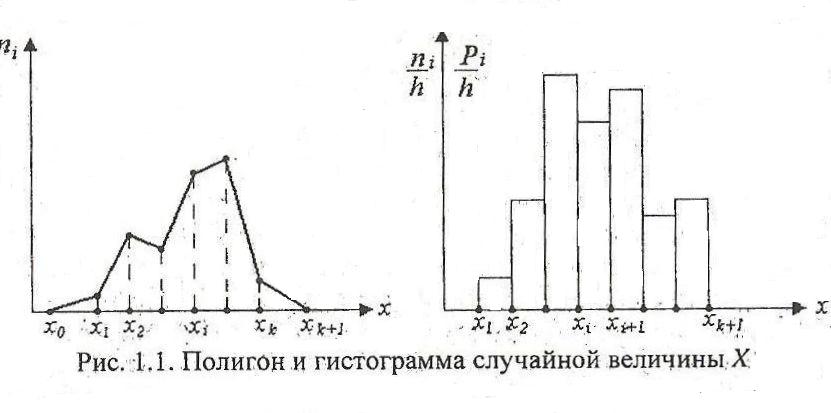
Интервальный ряд графически изображается в виде гистограммы (клеточного графика) распределения.
Гистограмма распределения - ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению ni/h (плотность частоты). В этом случае частота обезличивается и в каждом интервале ее можно отнести к любому значению признака. Площадь i - го прямоугольника равна ni, а площадь гистограммы равна объему выборки п.
Если частоты отнести к серединам интервалов и соединить ординаты прямыми, то получится полигон распределения.
Огива - графическое изображение рядов распределений по накопленным частотам.
В этом случае по оси абсцисс откладывают накопленные частоты (или частости), по оси ординат - значение признака по возрастающей величине. Соединяя точки, получают огиву распределения.
Корреляционная таблица - таблица, в которой представлена группировка по двум взаимосвязанным признакам: факторному и результативному. Концентрация частот около диагонали (любой) таблицы свидетельствует о наличии связи между признаками.
Пример 1.1. По 30 различным предприятиям области собраны статистические данные за прошедший год о доле (проценте) прибыли, направленной для выплаты дивидендов по своим акциям, и объеме средств (млн. руб.), выделенных на развитие производства (табл. 1.2).
Необходимо:
1) получить интервальный ряд, характеризующий распределение предприятий по сумме средств, направленных на развитие производства, образовав пять групп с равными интервалами;
2) построить корреляционную таблицу и аналитическую группировку для изучения связи между процентом прибыли для выплаты дивидендов по акциям и объемом средств, направленных на развитие производства.
Решение. Прибыль для выплаты дивидендов - это факторный признак X, а объем выделенных на развитие производства средств - результативный признак Y.
Для изучения структуры предприятия по объему средств, направленных на развитие производства, пользуясь данными табл. 1.2, построим интервальный вариационный ряд, характеризующий распределение предприятий по объему затраченных средств.
Величина интервала равна h = (ymax – ymin)/m,
где ymax , ymin - минимальное и максимальное значения величины Y.
т - количество интервалов.
Получаем: h = (36 – 6) / 5 = 6.0 млн.руб.
Путем прибавления величины интервала к минимальному уровню признака в группе получим группы предприятий по объему затраченных средств на развитие производства (табл. 1.3).
Данные группировки показывают, что 56.7 % предприятий затрачивают на развитие производства свыше 18 млн. руб.
Определим, существует ли зависимость между прибылью для выплаты дивидендов (факторный признак X) и размером затраченных средств (результативный признак Y).
Для этого построим корреляционную таблицу, образовав четыре группы по факторному и пять групп по результативному признакам (табл.1.4).
Таблица 1.2.
Показатели некоторых статей расхода средств предприятий области
| № предприятия | Прибыль для выплаты дивидендов по акциям, % | Объем средств, направленных на развитие производства, млн.руб. |
| 11,9 | 17,6 | |
| 16,3 | 11,4 | |
| 9,1 | 33,4 | |
| 11,4 | 29,6 | |
| 13,4 | 15,5 | |
| 21,7 | 10,0 | |
| 18,3 | 19,3 | |
| 15,5 | 6,0 | |
| 16,8 | 28,3 | |
| 12,0 | 21,5 | |
| 19,3 | 11,7 | |
| 13,6 | 23,5 | |
| 15,0 | 17,7 | |
| 14,0 | 27,0 | |
| 17,1 | 14,9 | |
| 8,7 | 25,5 | |
| 16,6 | 17,4 | |
| 15,3 | 24,6 | |
| 16,2 | 20,4 | |
| 18,6 | 9,5 | |
| 15,7 | 28,1 | |
| 14,4 | 24,0 | |
| 16,0 | 27,4 | |
| 18,2 | 12,0 | |
| 17,2 | 29,6 | |
| 10,8 | 36,0 | |
| 18,0 | 13,1 | |
| 11,5 | 31,8 | |
| 9,7 | 35,5 | |
| 20,4 | 10,7 |
Таблица 1.3.
Распределение предприятий по объему средств на развитие производства
| Номер группы | Объем средств на развитие производства, млн.руб. | Число предприятий | |
| в абсолютном выражении | в относительных единицах | ||
| I | 6 – 12 | 23,3 | |
| II | 12 – 18 | 20,0 | |
| III | 18 – 24 | 16,7 | |
| IV | 24 – 30 | 26,7 | |
| V | 30 - 36 | 13,3 | |
| Итого: | 100,0 |
Таблица 1.4.
Распределение предприятий по прибыли для выплаты дивидендов
и по объему средств на развитие предприятия
| Прибыль для выплаты дивидендов по акциям, % | Объем средств на развитие производства, млн.руб | ||||
| 6 - 12 | 12 - 18 | 18 - 24 | 24 - 30 | 30 - 36 | |
| 8,7 – 11,95 | |||||
| 11,95 – 15,2 | |||||
| 15,2 – 18,45 | |||||
| 18,45 – 21,7 |
Для построения корреляционной таблицы необходимо разбить прибыль для выплаты дивидендов по акциям на 4 интервала с шагом h = (21,7 – 8,7) / 4 = 3,25 %
Из данных корреляционной таблицы 1.4. видно, что распределение числа предприятий (частот) имеет место вдоль диагонали, проведенной из левого нижнего угла в правый верхний угол таблицы.
Уменьшение признака «прибыль для выплаты дивидендов, по акциям» сопровождалось увеличением признака «объем затраченных средств на развитие производства». Характер концентрации частот по указанной диагонали корреляционной таблицы, свидетельствует о, наличии обратной связи между изучаемыми признаками.
Установим наличие и характер связи между прибылью для выплаты дивидендов по акциям и объемом затраченных средств на развитие, предприятия методом аналитической группировки (табл. 1.5)
Для того чтобы рассчитать среднюю прибыль для выплат в группе необходимо сложить все значения прибыли по каждому предприятию группы и, поделить на количество предприятий в группе. По тому же принципу определяется средняя прибыль данной выборки в целом и средний объем затраченных средств на одно предприятие.Например, для первой,группы:
- средняя прибыль: (11,9+9,1+11,4+8,7+10,8+11,5+9,7)/7 = 10,4;
- объем средств: 17,6+33,4 + 29,6 + 25,5 + 36 + 31,8 + 35,5=209,4;
- в среднем на одно предприятие: 209,4 / 7 = 29,9.
Данные табл. 1.5 показывают, что с ростом прибыли для выплаты дивидендов по акциям, объем средств затрачиваемых на развитие производства, уменьшается. Следовательно, между исследуемыми признаками существует обратная зависимость.
Таблица 1.5
Зависимость объема затраченных средств на развитие производства от прибыли для выплаты дивидендов по акциям
| № п/п | Прибыль для выплаты дивидендов по акциям, % | Число предприятий в группе | Средняя прибыль для выплат в группе | Объем затраченных средств, млн.руб. | |
| всего | на одно предприятие | ||||
| I | 8,7 – 11,95 | 10,4 | 209,4 | 29,9 | |
| II | 11,95 – 15,2 | 13,7 | 129,2 | 21,5 | |
| III | 15,2 – 18,45 | 16,7 | 252,5 | 19,4 | |
| IV | 18,45 – 21,7 | 20,0 | 41,9 | 10,5 | |
| Итого: | 15,1 | 633,0 | 21,1 |
Вопросы для повторения
С какими науками и как связана эконометрика?
Каковы особенности эконометрического исследования?
Какие вопросы приходиться решать эконометристу?
Как определить величину интервала?
Резюме по теме
Результаты сводки и группировки материалов статистического наблюдения оформляются в виде статистических рядов распределения.
Статистический ряд распределения представляет собой упорядоченное расположение единиц изучаемой совокупности по какому-либо признаку.
Ряды распределения, образованные по атрибутивному признаку, называют атрибутивными.
Вариационные ряды распределения - ряды распределения, образованные по количественному признаку. Вариационный ряд предполагает расположение единиц совокупности в порядке возрастания (или убывания) значений признака.
Отдельное значение варьируемого признака, которое он принимает в вариационном ряду, называется вариантой. Численности отдельных вариант или групп вариационного ряда, показывающие, как часто встречаются те или иные варианты в ряду распределения, называют частотами.
Графическим способом изображения статистических данных называют их условное изображение при помощи точек, линий, плоскостей, геометрических фигур и условных знаков.
Дата добавления: 2017-09-19; просмотров: 900;
