Актуальность изучения экологии 7 страница

Динамичность экологических факторов во времени и пространстве зависит от астрономических, гелиоклиматических, геологических процессов, которые выполняют управляющуюроль по отношению к живым организмам. Животные и растения вынуждены приспосабливаться ко множеству факторов, причем эти приспособления вырабатываются и закрепляются в процессе эволюции и естественного отбора на генетическом уровне.

Эволюционно выработанные и наследственно закрепленные особенности живых организмов, обеспечивающие нормальную жизнедеятельность в условиях динамичных экологических факторов, называются адаптациями. Особи, не приспособленные к данным или изменяющимся условиям, вымирают.

Различают различные формы адаптации:

1) Морфологические адаптации. Примеры: приспособление формы тела организмов, обитающих в воде, к быстрому плаванию, например, у млекопитающих китообразных и рыбообразных акул, что характерно для жизненной формы; приспособление строения растений, обитающих в пустыне, к минимальной потере влаги за счет отсутствия листьев.

2) Физиологические адаптации. Они заключаются, например, в особенностях ферментативного набора в пищеварительном тракте животных, определяемого возможным составом пищи. Обитатели пустынь способны удовлетворять потребность во влаге путем биохимического окисления жиров.

3) Поведенческие (этологические) адаптации. Проявляются в различных формах. Так, существуют формы приспособительного поведения животных, направленные на обеспечение нормального теплообмена с окружающей средой: создание убежищ, передвижение с целью выбора оптимальных температурных условий. Например, суточные и сезонные кочевки млекопитающих и птиц.

Особенности поведения животных, как правило, направлены на то, чтобы избегнуть угрозы оказаться в экстремальных условиях. Это так называемый ²принцип минимальной амплитуды², согласно которому живой организм при прочных равных условиях выбирает такие местообитания, в которых обеспечивается минимальная амплитуда колебания одного или нескольких лимитирующих факторов среды.

Приспособительное поведение может проявляться у хищников в процессе выслеживания и преследования добычи, а у жертв – в определенных ответных реакциях (например, затаивание). Некоторые насекомые отпугивают хищников и паразитов резкими движениями. Чрезвычайно разнообразны поведенческие реакции млекопитающих и птиц в брачный период.

4. Популяция как компонент экосистемы

4.1. ПОПУЛЯЦИЯ, ЕЕ СТРУКТУРА И ДИНАМИКА

4.1.1. Понятие популяции в экологии

Живое население или, как его часто называют, биота экологической системы, представляет собой множество особей всех обитающих в ней растений, животных и микроорганизмов. Общая численность всех этих организмов чрезвычайно велика. Поэтому при изучении экосистем не может быть и речи об индивидуальном изучении каждой особи. Отдельные организмы объединяются (агрегируются) в группы на основе тех или иных признаков. Принципы выделения таких групп могут быть весьма разнообразными, однако наиболее естественным представляется агрегирование организмов, принадлежащих к одному биологическому виду, то есть деление биоты на видовые популяции.

Популяцией называют совокупность особей одного вида, в течение продолжительного времени населяющих определенное пространство, внутри которого осуществляется та или иная степень обмена генетической информацией (панмиксия).

Причины, заставляющие особей популяции группироваться в пределах ограниченных участков, чрезвычайно многочисленны и разнообразны, но главная из них состоит в неравномерности распределения экологических условий в географическом пространстве и в сходстве требований к этим условиям у организмов одного вида.

Так как внутри экосистемы не может быть каких-либо выраженных границ, затрудняющих панмиксию, то все организмы данного вида, обитающие в данной экосистеме, образуют единую популяцию. Сказанное дает основание сделать вывод о совпадении ареалов популяции с пространственными границами экосистем.

Системная экология изучает популяции как относительные самостоятельные подсистемы в рамках экосистемы, объединяющей их с абиотическими компонентами в единое динамическое целое. Следуя далее методологии системного подхода, у каждой популяции можно выделить основные системные атрибуты: состав, структуру и функционирование.

Очень часто популяция рассматривается как отдельная самостоятельная единица экосистемы, и различиями между особями популяции можно пренебречь, считая, что все они характеризуются одинаковыми средними показателями (размер биомасса и т. п.). Это и есть так называемый уровень полного внутрипопуляционного агрегирования. Иногда рассматривают уровни более слабого агрегирования, уже отражающие внутреннюю гетерогенность популяции по тем или иным признакам. В частности, широко используются уровни агрегирования, отвечающие группировкам по возрасту, полу и некоторым характерным генетическим признакам.

После выбора определенного уровня агрегирования каждая из выделенных групп в дальнейшем рассматривается как неделимый элемент, состояние которого описывается только агрегированными переменными, такими как, численность, средний размер, средняя биомасса особи.

Популяция обладает ²биологическими свойствами², присущими как популяции, так и составляющим ее организмам, и ²групповыми свойствами², присущими только группе в целом. Биологические свойства характеризуют жизненный цикл популяции: популяция, так же как и отдельный организм, растет, дифференцируется и поддерживает сама себя. Популяция имеет определенную организацию и структуру, которые можно описать.

В отличие от этого групповые свойства, такие, как рождаемость, смертность, возрастная структура и генетическая приспособленность, могут характеризовать только популяцию в целом. Таким образом, особь рождается, стареет, умирает, но применительно к особи нельзя говорить о рождаемости, смертности, возрастной структуре – характеристиках, имеющих смысл только на групповом уровне.

Каждая популяция имеет определенную структуру: возрастную (соотношение особей разного возраста), сексуальную (соотношение полов), пространственную (колонии, семьи, стаи и т. п.). Кроме того, каждая популяция, обитающая в том или ином месте, имеет определенную численность и амплитуду колебаний этой численности. Структура популяции, ее численность и динамика численности определяются экологической нишей данного вида и конкретно – соответствием условий местообитания (то есть режима факторов среды) требованиям (то есть толерантности) слагающих популяцию организмов. Поэтому, прямо или косвенно влияя на животный и растительный мир, человек всегда воздействует на популяции, меняет их параметры и структуру, зачастую нарушая их соответствие реальным режимам экологических факторов. В ряде случаев это может привести к гибели популяции.

Таким образом, охрана живой природы заключается в таком сохранении режимов экологических факторов, при котором не разрушаются экологические ниши, обеспечивается нормальное функционирование популяций живых организмов, соответствие их состава и структуры конкретным условиям место обитания.

4.1.2. Плотность и численность популяций

В любой природной системе поддерживается та численность особей в популяциях, которая в наибольшей степени отвечает интересам воспроизводства. Режим численности зависит от постоянно действующих регулирующих экологических факторов.

Для того, чтобы сравнить численность отдельных популяций или изменение численности одной и той же популяции в разные отрезки времени, целесообразно пользоваться таким относительным показателем, как плотность, то есть численность популяции, отнесенная к единице занимаемого ею пространства или среднее число особей на единицу площади или объема.

Зная изменение плотности во времени или пространстве, можно установить, увеличивается или уменьшается численность особей, представляет или нет данная популяция угрозу хозяйственным интересам. Динамика плотности популяций отражает сложные закономерности взаимоотношений между различными животными, между животными и растениями, поскольку все они являются биотическими факторами по отношению друг к другу. Кроме того, плотность зависит и от колебаний абиотических факторов среды.

Иногда бывает важно различать среднюю плотность, то есть численность (или биомассу) на единицу всего пространства, и удельную, или экологическую, плотность, то есть численность (или биомассу) на единицу обитаемого пространства (доступной площади или объема, которые фактически могут быть заняты популяцией).

Чем ниже трофический уровень, тем выше плотность, а чем крупнее животные внутри данного уровня, тем больше их биомасса. Так как у крупных животных интенсивность метаболизма на единицу массы меньше, чем у мелких, на данной энергетической базе может поддерживаться большая биомасса крупных животных.

4.1.3. Возрастной состав популяции

Возрастной состав популяции

Возрастная структура популяции может изменяться и без изменения ее численности.

По мере развития человеческого общества от состояния освоения новых территорий и быстрого роста численности к зрелому состоянию стабильной популяции процент населения в младших возрастных классах уменьшается. Это изменение возрастной структуры и увеличение процента населения старших возрастных классов оказывает глубокое воздействие на жизненный уклад общества и экономику.

Упрощенно в популяции можно выделить три экологические возрастные группы: пререпродуктивную, репродуктивную и пострепродуктивную. Длительность этих возрастов по отношению к общей продолжительности жизни сильно варьирует у разных организмов. У современного человека три эти возрастные периоды приблизительно одинаковы, на каждый из них приходится около трети жизни. У первобытных людей пострепродуктивный период был намного короче. Для многих животных и растений характерен очень длительный пререпродуктивный период. У некоторых животных, в особенности у насекомых, пререпродуктивный период чрезвычайно длителен, репродуктивный период очень короткий, а пострепродуктивный период отсутствует совсем.

4.1.4. Пространственная структура популяции

Распределение особей в популяции может быть: 1) случайным, 2) равномерным (более регулярным, чем при случайном распределении) и 3) групповым (нерегулярным и неслучайным). Случайное распределение наблюдается тогда, когда среда очень однородна, а организмы не стремятся объединиться в группы. Равномерное распределение встречается там, где между особями очень сильна конкуренция или существует антагонизм, способствующий равномерному распределению в пространстве. Чаше всего наблюдается образование различного рода скоплений. Однако если особи в популяции обладают тенденцией образовывать группы определенной величины, то распределение самих групп может оказаться более близким к случайному или даже равномерному.

Агрегация особей в группы может происходить по следующим причинам:

7) вследствие локальных различий в местообитаниях;

8) под влиянием суточных и сезонных изменений погодных условий;

9) в связи с процессами размножения;

10) в результате социального привлечения (у высших животных).

Агрегация может усиливать конкуренцию между особями за компоненты минерального питания, пищу или пространство, но это часто более чем уравновешивается повышением жизнеспособности группы, поскольку группа обладает большими возможностями для своей защиты, обнаружения ресурсов или изменения микроклимата.

Степень агрегации, так же как общая плотность, при которой наблюдается оптимальный рост и выживание популяции, варьирует у разных видов и в разных условиях; поэтому как «недонаселенность» (отсутствие агрегации), так и перенаселенность могут оказывать лимитирующее влияние. Это и есть так называемый принцип Олли.

Особый тип агрегации был назван «образованием безопасных поселений». В этом случае обширные, социально организованные группы животных обосновываются в благоприятном центрально расположенном участке, откуда они регулярно расходятся для удовлетворения потребностей в пищевой или других видах энергии и куда возвращаются. Некоторые из наиболее успешно адаптирующихся животных на земле, в том числе скворцы и человек, используют эту стратегию.

4.1.5. Закономерности динамики популяций. Описание популяций на уровне полного внуприпопуляционного агрегирования

Численность живых организмов, населяющих ту или иную экосистему, не бывает постоянной, а всегда колеблется в более или менее широких пределах. Эти колебания имеют очень важное значение для человека, поскольку многие животные и растения служат объектами его хозяйственной деятельности или причиной какого-либо ущерба. Поэтому знание закономерностей динамики численности популяций необходимо для прогнозирования возможных нежелательных явлений и внесения в случае необходимости корректив в эту динамику с целью управления ею.

Динамику изменения популяции принято характеризовать скоростью изменения численности популяции. Для любой i-ой популяции в экосистеме ее численность x_i подчиняется следующему дифференциальному уравнению:

,

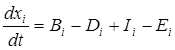где B_i – скорость размножения в i-ой популяции,

D_i – скорость смерти в i-ой популяции,

I_i – скорость иммиграции для i-ой популяции,

E_i – скорость эмиграции для i-ой популяции.

Таким образом, изменение плотность x_i происходит в результате взаимодействия четырех процессов: размножения, гибели, иммиграции и эмиграции. Поскольку протекание каждого из этих процессов может зависеть как от плотности численности самой данной популяции x_i, так и от остальных абиотических - биотических факторов экологического пространства, то указанные скорости этих процессов являются функциями, заданными на рассматриваемом экологическом пространстве:

B_i = B_i(v₁,…,v_m, x₁,…,x_n)

D_i = D_i(v₁,…,v_m, x₁,…,x_n)

I_i = I_i(v₁,…,v_m, x₁,…,x_n)

E_i = E_i(v₁,…,v_m, x₁,…,x_n),

где v₁,…,v_m – экологические факторы среды, а x₁,…,x_n – численности популяций в экосистеме.

Поскольку решать представленное дифференциальное уравнение в общем виде сложно, то будем рассматривать относительно изолированные в биотическом отношении экосистемы, для которых скоростями иммиграции I_i и эмиграции Е_i можно пренебречь и представить уравнение динамики плотности популяции в более простом виде:

.

Опираясь на концепцию полного внутрипопуляционного агрегирования, абсолютные скорости размножения и гибели можно представить в виде произведения плотности популяции на соответственные удельные скорости:

B_i(…) = b_i(…) x_i

D_i(…) = d_i(…) x_i ,

где b_i(…)и d_i(…) – удельные скорости размножения и гибели, называемые соответственно функциями рождаемости и смертности.

Отделить влияние процессов размножения и гибели на динамику популяции часто весьма затруднительно, вследствие чего вводится их результирующая – удельная скорость изменения популяции (удельная скорость роста):

r_i = b_i - d_i .

Таким образом, основное уравнение динамики популяции можно записать в виде:

.

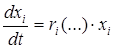Для многих видов на начальном этапе роста популяции, при малой плотности x_i величина r_i практически не зависит от самого значения x_i. Это позволяет записать аналитическое решение рассматриваемого дифференциального уравнения в виде

.

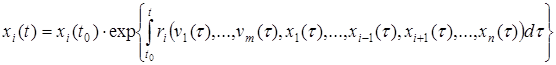Здесь t₀ – некоторый начальный фиксированный момент времени, для которого известно значение численности популяции.

Важнейшей экологической характеристикой, отражающей способность популяций, обусловленную внутренними свойствами образующих ее элементов – особей, к увеличению численности при оптимальных экологических условиях, является максимальное значение r_i:

.

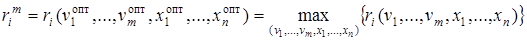Величину называют биотическим потенциалом данного вида.

Если в течение рассматриваемого периода t₀ £ t £ t будут поддерживаться условия, при которых реализуется максимальное значение удельной скорости прироста, равное , то, вынося постоянную величину из-под знака интеграла и интегрируя, получаем уравнение кривой максимально быстрого роста популяции данного вида, когда он полностью раскрывает свой биотический потенциал:

.

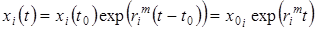Вводя коэффициент умножения плотности i-ой популяции за единицу времени Dt = 1 в виде

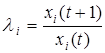
и применяя его к экспоненциально растущей популяции с биотическим потенциалом , получаем, что l_i и связаны соотношением

l_i = exp(r_i^m) или r_i^m = ln l_i.

Используя коэффициент умножения за единицу времени l_i, уравнение экспоненциального роста можно представить в форме

,

то есть уравнением геометрической прогрессии с первым членом x_i(t₀) и показателем l_i.

На способность популяций увеличивать свою численность в соответствии с геометрической прогрессией указывали еще древние египтяне и греки, затем об этом писали Макиавелли (1525 г.) и Бюффон (1751 г.). Ч. Дарвин распространил идею геометрического роста на все виды животных и растений, положив постулат о высоком репродуктивном потенциале видов в основу своей теории естественного отбора.

На практике экспоненциальный рост численности популяции рано или поздно заканчивается. Это объясняется снижением величины r_j по сравнению с r_j^m вследствие отклонения экологических факторов от оптимальных или достижения такой плотности популяции, когда становится существенным влияние зависящих от плотности факторов, приводящих к снижению рождаемости и увеличению смертности.

По мере увеличения плотности усиливается действие тормозящих рост внешних и внутренних факторов. В результате этого плотность поддерживается на некотором свойственном данной экосистеме уровне, называемом «емкостью среды» по отношению к этой популяции, отклоняясь от нее в ту или иную сторону под действием различных факторов (прежде всего, экзогенных метеорологических).

Наиболее распространенной формой влияния плотности следует признать падение рождаемости и монотонное увеличение смертности по мере возрастания плотности популяции, что приводит к убыванию r_i с ростом плотности x_i, причем характер убывания определяется соотношением кривых b_i(…,x_i,…) и d_i(…,x_i,…).

Простейшая зависимость удельной скорости прироста от плотности популяции, приводящая к S-образному виду кривой динамики, может быть получена при постоянной рождаемости и смертности, линейно возрастающей с ростом плотности:

,

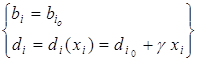где – независящая от плотности минимальная смертность, а g – коэффициент пропорциональности. При этом разность рождаемости и минимальной смертности есть максимальная удельная скорость роста 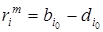. Тогда

.

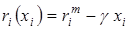Если ввести обозначение

,

то можно записать, что

.

Используя эту зависимость, приходим к общепринятой форме уравнения динамики популяции в среде с ограниченными ресурсами:

.

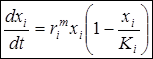Это уравнение называется уравнением Ферхюльста-Перла в честь бельгийского ученого П. Ферхюльста, который впервые предложил его для описания динамики человеческого населения (1838), и американского эколога Р. Пёрла (1920), который также получил это уравнение и широко использовал его для описания динамики биологических популяций. Кроме того, учитывая исторический приоритет, это уравнение называют логистическим, как это делал сам П. Ферхюльст.

Чтобы получить аналитическое решение логистического уравнения, запишем его в виде

,

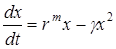где 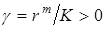– называется коэффициентом внутривидовой конкуренции. Для интегрирования перепишем его в виде

.

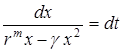Отсюда

.

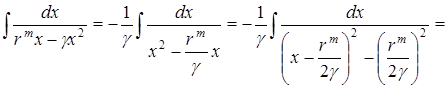
Учитывая то, что начальное условие имеет вид x₀ = x(t₀), получаем

.

Отсюда

и далее

.

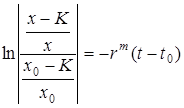Или это можно записать в виде

,

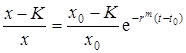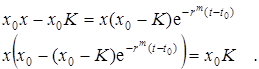
Окончательно получаем решение логистического уравнения в виде:

.

Для анализа поведения этой функции нам надо знать, как ведет себя вторая производная:

.

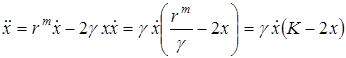Таким образом, вторая производная 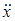обращается в ноль при x = К/2. Это точка перегиба S-образной кривой. Если x₀ > К/2, то логистическая кривая выпуклая; если x₀ < К/2, то для x₀ < x < К/2 логистическая кривая вогнутая, а для K/2 < x < K эта кривая – выпукла.

Логистическое уравнение имеет аналитическое решение, которое может быть записано как

,

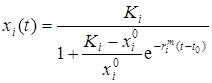и определяется тремя независимыми параметрами 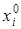, К_i и r_i^m.

Первый из них ( 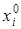) указывает начальное значение численности x_i при t = t₀, второй – высоту плато насыщения, к которому стремится x_i(t) при t ® t₀ (то есть предельную для данного вида численность популяции), а r_i^m задает крутизну начального роста.

Чтобы выяснить экологическое содержание коэффициентов r_i^m и К_i, следует обратить внимание на то, что зависимость удельной скорости прироста от плотности популяции вида

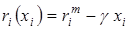
представляет собой разложение удельной скорости роста в ряд Тейлора по степеням от плотности популяции x_i, представленное нулевой и первой степенью. Компонента этого разложения, соответствующая нулевой степени, 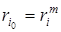не зависит от плотности x_i, а компонента, соответствующая первой степени, 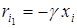зависит от плотности x_i, причем при x_i ® 0 имеем 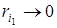. Поэтому при малой исходной плотности x_i⁰ начальный рост популяции будет почти экспоненциальным с показателем экспоненты r_i^m, так что этот параметр является не чем иным, как биотическим потенциалом рассматриваемой популяции. Таким образом, рост практически каждой популяции на начальном этапе описывается J-образной (экспоненциальной) кривой.

С возрастанием времени второе слагаемое в знаменателе формулы для логистической кривой стремится к нулю ( 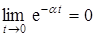при a ® 0), в результате чего решение x_i(t) асимптотически приближается к К_i. Таким образом, параметр К_i характеризует емкость среды по отношению к данной популяции и выражается в соответствующей данной емкости среды предельной численности этой популяции. Только при исследовании динамики роста популяции за большой период времени становится очевидным ее S-образный или сигмоидный характер.

Иногда еще верхний предел увеличения численности популяции, соответствующий константе К_i, называется верхней асимптотой сигмоидной кривой. Ее называют также пределом роста.

Как показывают экспериментальные исследования, подбирая коэффициенты 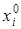, К_i и r_i^m, можно более или менее удовлетворительно описывать динамику популяций разных организмов – от одноклеточных до высших представителей растительного и животного мира.

Уравнение логистического роста следует рассматривать как одну из возможных моделей описания популяционной динамики. S-образная кривая и, в частности, логистическая, форма кривых роста характерна для популяций, существующих в относительно постоянных внешних условиях, когда допустимо рассматривать в качестве удельной скорости изменения r_i частную функцию отклика на плотность популяции x_i