Актуальность изучения экологии 9 страница
 .
.
Поскольку функция fi(…) представима в виде
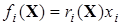 ,
,
то при i ¹ j имеем
 ,
,
а при i = j имеем
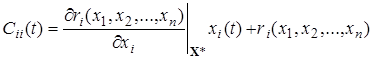 .
.
Таким образом, матрица С(t) = êêСij(t) êê (i = 1..n, j = 1...n) даёт исчерпывающую количественную характеристику всей совокупности биотических отношений между популяциями биоценоза в рассматриваемый момент времени t и поэтому называется структурной матрицейбиоценоза.
Для системы Лотки-Вольтерра элементы структурной матрицы в стационарной точке Х* имеют вид
 ;
; 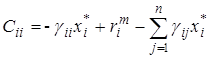 .
.
Теперь вопрос о локальной устойчивости точки Х* может быть решён путём применения одного из известных критериев, например, критерия Рауса-Гурвица.
4.2.4. Классификация биотических взаимодействий
Структурную матрицу биоценоза С(t) удобно использовать для классификации биотических взаимодействий между видами. Рассматривая пару видов (i,j), качественную характеристику взаимодействий между ними характеризуют парой знаков элементов структурной матрицы биоценоза Сij и Сji, то есть вводят в рассмотрение пару символов
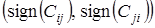 ,
,
каждый из которых может принимать значения "+", "0" или "-", в зависимости от направления влияния численности одного вида на скорость роста другого вида.
Выделяют следующие пары взаимодействий видов:
| влияние первого вида на второй | влияние второго вида на первый | ||
| 1. | Нейтрализм | ||
| 2. | Аменсализм | - | |
| 3. | Комменсализм | + | |
| 4. | Конкуренция | - | - |
| 5. | Жертва-эксплуататор | + | - |
| 6. | Паразитизм | + | - |
| 7. | Протокооперация | + | + |
| 8. | Мутуализм | + | + |
4.2.5. Аменсализм (-, 0)
К этому типу взаимодействия ((-,0) или (0,-)) относятся межвидовые отношения самой различной природы, проявляющиеся в том, что один из видов взаимодействующей пары в биоценозе оказывает отрицательное воздействие на рост другого (С21 < 0), хотя сам не испытывает существенного влияния с его стороны (С12 » 0).
Аменсализм во взаимоотношениях растений связан с выделением одним из видов органического ингибитора, подавляющего рост другого вида; во взаимоотношениях микроорганизмов – с выделением одним из видов специфического вещества – антибиотика, отрицательно воздействующего на другие микроорганизмы (антибиоз), во взаимоотношениях между микроорганизмами, растениями и животными – с выделением одним из видов токсинов.
Динамика двухвидовой системы с аменсализмом описывается системой уравнений

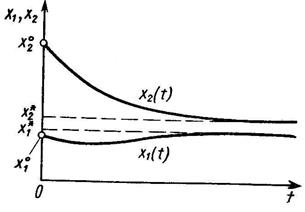
где K2 – ёмкость среды для второго вида при отсутствии первого, а коэффициент a21 показывает, на сколько уменьшается ёмкость среды при увеличении плотности первого вида на единицу. При К2/К1 > a21 существует единственное устойчивое стационарное состояние 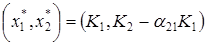 , при котором сосуществуют оба вида и к которому сходятся решения из любого начального состояния ( x10, x20 ) > 0. При К2/К1 < a21 система имеет единственное устойчивое стационарное состояние ( х1* , х2* ) = ( К1, 0), при котором численность второго вида равна нулю.
, при котором сосуществуют оба вида и к которому сходятся решения из любого начального состояния ( x10, x20 ) > 0. При К2/К1 < a21 система имеет единственное устойчивое стационарное состояние ( х1* , х2* ) = ( К1, 0), при котором численность второго вида равна нулю.
На фазовой плоскости для анализа траекторий системы строят две линии, на которых одна из компонент скорости изменения обращается в ноль:
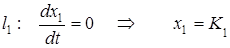
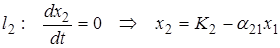 .
.
 |
Таким образом, если коэффициент ингибирования a21 относительно мал (a21< К2/К1), оба вида могут существовать, хотя стационарное значение численности аменсала снижается (по сравнению с К2) до более низкого значения К2 - a21К1. Если же коэффициент ингибирования достаточно велик (a21 > К2/К1), то происходит полное вытеснение вида-аменсала.
4.2.6. Комменсализм (+, 0)
К этой категории относятся разнообразные случаи отношений между двумя видами, когда первый вид, называемый «хозяином», положительно воздействует на второй, называемый «комменсалом», хотя последний никак не влияет на «хозяина». Наиболее распространенная форма комменсализма, (которую, порой, не совсем правильно называют «нахлебничеством»), когда комменсал тем или иным способом получает от хозяина пищу, обеспечивая тем самым свое существование. Кроме того, положительное влияние хозяина на комменсала может заключаться в предоставление жилища («квартиранство»), укрытия, места для прикрепления; наконец, хозяин может способствовать распространению и размножению комменсала, выполняя роль переносчика его взрослых особей или зародышей («форезия»).
В зависимости от способности комменсала существовать самостоятельно, не пользуясь услугами хозяина, различают факультативный и облигатный комменсализм.
Математическая модель облигатного комменсализма имеет вид:
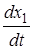 = r1x1 (1 -
= r1x1 (1 - 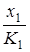 )
)
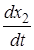 = r2x2 (1 -
= r2x2 (1 -  ) ,
) ,
где K2 – емкость среды для комменсала при отсутствии хозяина,  – коэффициент, показывающий, насколько увеличится K2(x1) = K2 +
– коэффициент, показывающий, насколько увеличится K2(x1) = K2 + x1 при увеличении плотности x1 на единицу. Для этой модели существует единственное устойчивое состояние (
x1 при увеличении плотности x1 на единицу. Для этой модели существует единственное устойчивое состояние ( 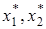 ) = ( K1, K2 +
) = ( K1, K2 +  K1).
K1).
|
|
4.2.7. Мутуализм (+, +)
Отношением мутуализма между двумя видами называется взаимно положительное влияние их друг на друга, которое, в конечном счете, проявляется в том, что увеличение численности любого из них вызывает увеличение скорости роста численности другого.
Иногда путают понятия мутуализма и симбиоза. В строгом смысле термин «симбиоз» охватывает все случаи тесного и устойчивого сожительства организмов разных видов, то есть комменсализм, эксплуатацию (паразитизм) и мутуализм. В то же время, некоторыми авторами это понятие применяется в более узком смысле, как синоним мутуализма.
Мутуалистические отношения между видами достаточно широко распространены в природе и играют заметную роль в функционировании и эволюции экосистем. Одним из ярких примеров мутуализма в природе является лишайник, который, как оказалось, представляет собой взаимовыгодное сожительство водоросли и гриба. Особенно важными с точки зрения влияния на функционирование экосистем являются мутуалистические взаимодействия зеленых растений (главных производителей органического вещества) с азотофиксирующими микроорганизмами (прокариотами) и грибами, которые осуществляют биологическую фиксацию атмосферного азота.
При математическом описании динамики мутуализма целесообразно, также как для аменсализма и комменсализма, исходить из логистического уравнения. Если взаимное влияние вида проявляется в том, что при увеличении численности каждого из них пропорционально увеличиваются и ёмкость среды для другого (например, путем образования новых укрытий, мест для прикрепления, гнездования), то динамика численности видов хорошо описывается системой дифференциальных уравнений вида:
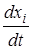 = xiri (1 -
= xiri (1 - 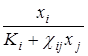 ) (i = 1,2; i
) (i = 1,2; i 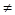 j),
j),
где коэффициенты χij > 0, фигурирующие в знаменателе, показывают, на сколько увеличится емкость среды для i-го вида при увеличении численности j-го на единицу.
В других случаях взаимодействие симбионтов может происходить таким образом, что каждый производит вещества, необходимые для роста другого, и для описания динамики популяций удобна другая (эквивалентная) форма логистического уравнения
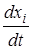 = xi (ri -
= xi (ri - 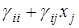 ) (i = 1,2; i
) (i = 1,2; i 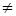 j),
j),
 |
где
 =
= 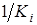 – определяет самолимитирование i-го вида, а коэффициент
– определяет самолимитирование i-го вида, а коэффициент 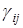 показывает на сколько изменяется удельная скорость роста i-го вида при изменении численности j-го на единицу.
показывает на сколько изменяется удельная скорость роста i-го вида при изменении численности j-го на единицу.
При биологически содержательных значениях параметров ri, Ki, χij, 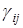 > 0 рассматриваемые системы дифференциальных уравнений характеризуются наличием единственной устойчивой стационарной точки, координаты которой в первом случае равны
> 0 рассматриваемые системы дифференциальных уравнений характеризуются наличием единственной устойчивой стационарной точки, координаты которой в первом случае равны
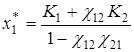 ;
;  ;
;
а во втором
 ;
; 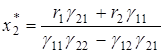 .
.
Фазовый портрет системы уравнений мутуализма имеет вид, приведенный на рисунке.
4.2.8. Конкуренция в широком смысле или интерференция (-, -)
Конкуренцией в широком смысле (предпочтительнее употреблять термин «интерференция») называют любое взаимно отрицательное отношение между видами. Её частными случаями являются: 1) конкуренция (в узком смысле слова) за тот или иной ограниченный ресурс (соперничество); 2) взаимное аллелопатическое ингибирование (антагонизм) и 3) непосредственная «борьба» между представителями разных видов (агрессия).
Вначале рассмотрим простейшую модель взаимодействия двух видов в условиях конкуренции за общий ресурс (пищу). Выразим коэффициент прироста каждой из популяций в виде
ri = 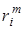 -
- 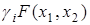 (i = 1, 2),
(i = 1, 2),
где 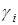 – положительный коэффициент, характеризующий потребность в пище каждого из видов; F(x1, x2) – скорость потребления пищи. Предположим, что функция F(x1, x2) обращается в нуль при x1 = 0 и x2 = 0 и монотонно неограниченно возрастает по каждой из переменных.
– положительный коэффициент, характеризующий потребность в пище каждого из видов; F(x1, x2) – скорость потребления пищи. Предположим, что функция F(x1, x2) обращается в нуль при x1 = 0 и x2 = 0 и монотонно неограниченно возрастает по каждой из переменных.
Тогда динамика развития популяций может быть описана системой дифференциальных уравнений

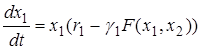
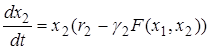 .
.
Перепишем её в виде

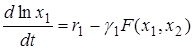
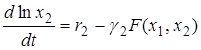 .
.
Исключая отсюда функцию F(x1, x2), получим
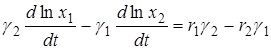
или
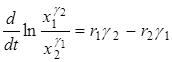 .
.
Решение этого уравнения имеет вид
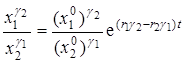 ,
,
где  и
и  – численности популяций в начальный момент времени t = 0.
– численности популяций в начальный момент времени t = 0.
Прежде всего, следует отметить, что указанные решения системы должны быть ограничены на бесконечности, то есть при 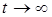 . Это связано с тем, что в силу монотонного неограниченного возрастания функции
. Это связано с тем, что в силу монотонного неограниченного возрастания функции 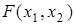 по каждой из переменной при
по каждой из переменной при 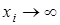 обязательно наступит момент, когда скорость изменения xi станет меньше нуля, то есть xi начнет убывать.
обязательно наступит момент, когда скорость изменения xi станет меньше нуля, то есть xi начнет убывать.
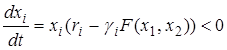 .
.
Для дальнейшего анализа полученного решения положим для определенности, что 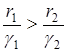 . Тогда отношение
. Тогда отношение 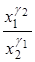 будет бесконечно возрастать, то есть
будет бесконечно возрастать, то есть 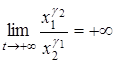 . Отсюда в силу ограниченности x1 и x2 получаем, что
. Отсюда в силу ограниченности x1 и x2 получаем, что 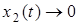 .
.
Это означает, что численность второй популяции, для которой значение 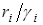 меньше, убывает, стремясь к нулю, в то время, как численность первой стремится к значению, определяемому из уравнения
меньше, убывает, стремясь к нулю, в то время, как численность первой стремится к значению, определяемому из уравнения 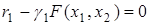 . Это подтверждает интуитивный вывод о том, что исчезает вид, обладающий меньшим коэффициентом естественного прироста и более чувствительный к нехватке пищи.
. Это подтверждает интуитивный вывод о том, что исчезает вид, обладающий меньшим коэффициентом естественного прироста и более чувствительный к нехватке пищи.
Полученные результаты также подтверждают известный принцип Гаузе, согласно которому два вида с одинаковыми экологическими потребностями не могут сосуществовать в одном месте обитания.
Необязательно два конкурирующих вида не могут сосуществовать вместе и один из видов должен исчезнуть. Указанный результат был получен для простейшей модели, не учитывающей саморегуляцию численности видов. Рассмотрим случай конкуренции с саморегуляцией, описываемой логистическим уравнением, когда взаимодействие видов несимметрично и описывается линейной функцией вида
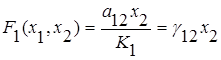 ;
; 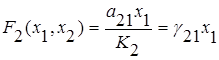 .
.
Это так называемая модель Лотки-Вольтерра для двухвидовой системы с конкуренцией
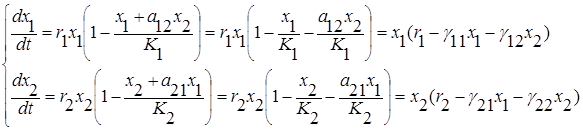
где ri – удельная скорость роста и Ki – ёмкость среды для i-го вида при отсутствии конкуренции, а положительные безразмерные коэффициенты а12 и а21 служат мерой относительного влияния видов друг на друга; 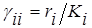
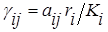 (i =1,2; i¹j).
(i =1,2; i¹j).
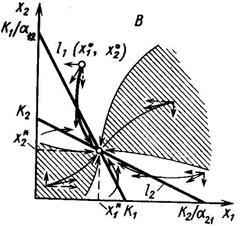
Поведение решений данной системы удобно охарактеризовать с помощью метода фазовых портретов на плоскости с координатами (x1, x2). В каждой точке траектории решения (x1(t), x2(t)) на фазовой плоскости может быть отображён вектор скорости, имеющий координаты 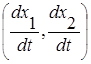 , то есть правые части системы дифференциальных уравнений определяют вектор скорости.
, то есть правые части системы дифференциальных уравнений определяют вектор скорости.
Как видно из указанной системы, знаки производных dx1/dt и dx2/dt совпадают со знаками линейных функций
l1(x1, x2) = k1 - x1 - a12x2
l2(x1, x2) = k2 - x2 - a21x1
и эти же линейные функции определяют на фазовой плоскости геометрическое место точек, где указанные производные обращаются в нуль, в виде линейных уравнений:
| l1(x1, x2) = k1 - x1 - a12x2 = 0 Þ x1 = k1 - a12x2 |
| l2(x1, x2) = k2 - x2 - a21x1 = 0 Þ x2 = k2 - a21x1 . |
При этом производная  будет положительной под прямой li(x1, x2) = 0, равной нулю – на прямой, и отрицательной – над ней. Используя эти данные, в каждой точке (x1, x2) мы можем качественно определить направление движения на проходящей через неё траектории.
будет положительной под прямой li(x1, x2) = 0, равной нулю – на прямой, и отрицательной – над ней. Используя эти данные, в каждой точке (x1, x2) мы можем качественно определить направление движения на проходящей через неё траектории.
Если пренебречь вырожденными случаями параллельности и совпадения, то возможны следующие четыре варианта взаимного расположения прямых l1 и l2 на фазовой плоскости:
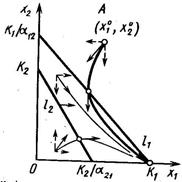
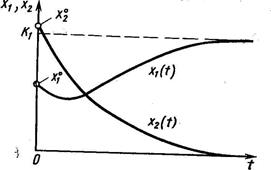
1. Прямая l1 располагается целиком выше l2, то есть 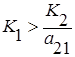 и
и  , что эквивалентно
, что эквивалентно 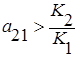 и
и 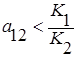 . Первый вид как более сильный конкурент всегда будет вытеснять второй, независимо от их начальных численностей (
. Первый вид как более сильный конкурент всегда будет вытеснять второй, независимо от их начальных численностей ( 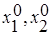 ).
).
| 
|
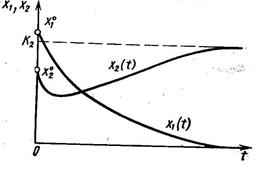
2. Прямая l2 целиком лежит выше l1, то есть 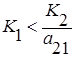 и
и 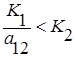 , что эквивалентно
, что эквивалентно  и
и 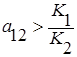 . Всегда побеждает второй вид.
. Всегда побеждает второй вид.

| 
|
3. Прямые l1 и l2 пересекаются в положительном квадранте и при этом l1 падает круче, чем l2, то есть 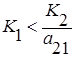 и
и  , что эквивалентно
, что эквивалентно  и
и 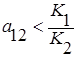 . Существует единственное положение равновесия (
. Существует единственное положение равновесия ( 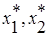 ), координаты которого удовлетворяют системе линейных уравнений
), координаты которого удовлетворяют системе линейных уравнений
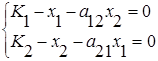
и равны
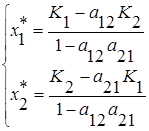
и которое устойчиво, так что из любого начального состояния 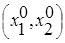 система с течением времени переходит в равновесное состояние (
система с течением времени переходит в равновесное состояние ( 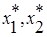 ), характеризуемое нулевыми численностями обоих видов.
), характеризуемое нулевыми численностями обоих видов.
| 
|
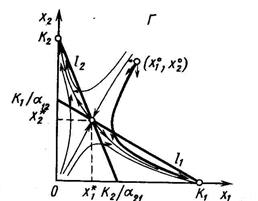
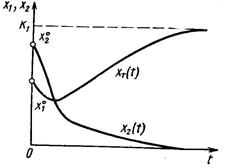
4. Прямые l1 и l2 пересекаются в положительном квадранте так, что l2 падает круче, чем l1 то есть 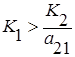 и
и 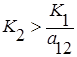 , что эквивалентно
, что эквивалентно 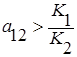 и
и 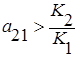 . Исход конкуренции определяется начальным соотношением численностей, в зависимости от начального соотношения плотностей
. Исход конкуренции определяется начальным соотношением численностей, в зависимости от начального соотношения плотностей 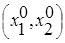 произойдёт вытеснение первого или второго вида.
произойдёт вытеснение первого или второго вида.
| 
|
4.2.9. Понятие экологической ниши и уравнения конкуренции
Пусть V – пространство экофакторов. Предположим, что ресурс, потребляемый входящими в сообщество популяциями, характеризуется вектором 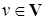 , а его объём ограничен величиной K(v). Функцию K(v) обычно называют спектром ресурса. Потребление ресурса видом і характеризуется функцией предпочтения fi(v), называемой часто функцией потребления. Наиболее предпочитаемый ресурс vi, соответствующий максимальному значению функции fi, принято называть центром ниши.
, а его объём ограничен величиной K(v). Функцию K(v) обычно называют спектром ресурса. Потребление ресурса видом і характеризуется функцией предпочтения fi(v), называемой часто функцией потребления. Наиболее предпочитаемый ресурс vi, соответствующий максимальному значению функции fi, принято называть центром ниши.
Пусть xi(t) – численность (биомасса) популяции i в момент времени t. Тогда произведение fi(v)xi(t) описывает объём ресурса v, потребляемого видом i. Разность 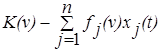 указывает на потенциальную возможность сосуществования популяций, потребляющих ресурс v. Если эта разность достаточно велика, то можно считать, что численность популяции увеличивается в соответствии с законом
указывает на потенциальную возможность сосуществования популяций, потребляющих ресурс v. Если эта разность достаточно велика, то можно считать, что численность популяции увеличивается в соответствии с законом 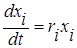 (i=1,2,…,n).
(i=1,2,…,n).
Будем считать, что на рост популяции влияет относительная истощённость ресурса в точке v, равная
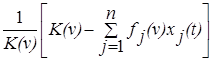 .
.
При этом динамика численности популяции i будет описываться уравнением
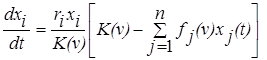 .
.
Обозначим  . Выражение Ki имеет смысл общего объёма ресурсов, потребляемых видом i и называется ёмкостью ниши. Умножив уравнение на fi(u) и проинтегрировав по всему пространству ресурсов V, получим
. Выражение Ki имеет смысл общего объёма ресурсов, потребляемых видом i и называется ёмкостью ниши. Умножив уравнение на fi(u) и проинтегрировав по всему пространству ресурсов V, получим
 ,
,
где  называются коэффициентами конкуренции. Обозначив
называются коэффициентами конкуренции. Обозначив 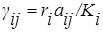 , запишем уравнение конкуренции следующим образом :
, запишем уравнение конкуренции следующим образом :
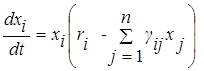 .
.
Эта система является диссипативной, поскольку при 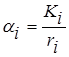 квадратичная форма
квадратичная форма
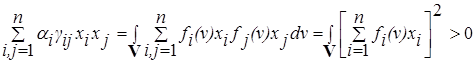
при всех x ¹ 0.
 Таким образом, если существует положительное решение системы уравнений GC = Rс коэффициентами из выше рассмотренного уравнения конкуренции, то оно является положением равновесия, асимптотически устойчивым в целом в положительном ортанте
Таким образом, если существует положительное решение системы уравнений GC = Rс коэффициентами из выше рассмотренного уравнения конкуренции, то оно является положением равновесия, асимптотически устойчивым в целом в положительном ортанте 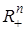 .
.
Пусть функция потребления имеет гауссовский вид:
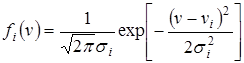 ,
,
где 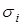 – дисперсия нормального распределения.
– дисперсия нормального распределения.
Обозначим через dij расстояние между центрами vi и vj. Тогда коэффициенты конкуренции принимают вид
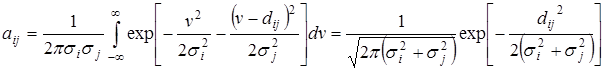
Если все распределения имеют одинаковую дисперсию 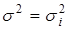 и
и 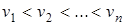 , то
, то  ,
,
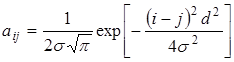 .
.
Дата добавления: 2017-09-19; просмотров: 446;


