Актуальность изучения экологии 8 страница

,

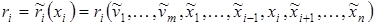отвечающую фиксированным значениям остальных экологических факторов:

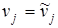
	для j = 1,…,m
	для j = 1,…,n, кроме j = i .

Если же в течении рассматриваемого периода значения этих факторов существенно изменяются, картина динамики плотности может заметно отличатьсяот S-образной, отражая все разнообразие хода изменения экзогенных для всей экосистемы или внутриэкосистемных, но внешних по отношению к данной популяции факторов . Среди экзогенных факторов, определяющих динамику многих популяций, решающая роль принадлежит метеорологическим показателям, поскольку они, как правило, не постоянны по времени и имеют ярко выраженную сезонную изменчивость.

4.2. БИОЦЕНОЗ ЭКОСИСТЕМЫ

4.2.1. Динамика биоценоза как результат межвидовых взаимодействий

Понятие о биоценозе, введенное К. Мёбиусом в 1877 г., сыграло важную роль в становлении системной концепции в экологии, сосредоточивая внимание исследователей на взаимодействиях между видами и возникающими вследствие этого целостными свойствами биологических сообществ. В отношении биоценоза сложились разные представления – от точки зрения Ф. Клементса (1928) и его последователей на биотическое сообщество как на организм высшего порядка (суперорганизм) до практического отрицания объективных оснований для концепции биоценоза в работах Л. Г. Раменского (1924), Г. Глизона (1926) и других исследователей.

В нашем понимании биоценоз – это совокупность всех популяций биологических видов, принимающих существенное участие в функционировании данной экосистемы. То есть биоценоз – это живая часть экосистемы.

В каждый момент времени t биоценоз имеет определенное видовое богатство (видовую насыщенность), которое измеряется числом входящих в него популяций различных видов – n(t), и количественный состав, характеризуемый набором из n(t) чисел x₁(t),…,x_n(t)(t), обозначающих численности или плотности этих популяций.

Среди разнообразных группировок видов в пределах биоценоза наибольшее теоретическое и практическое значение имеют консорции, выделяемые на основе трофических и топических отношений, и гильдии, отражающие функциональную близость между видами.

Консорцией называется совокупность видов, связанных пищевыми или прочими (топическими, фабрическими и др.) связями с некоторым видом, называемым эдификатором или детерминантом консорции, в качестве которого обычно выступает растение-автотроф. Гильдия определяется как группа видов, использующих один и тот же класс ресурсов среды одинаковым способом. Таким образом, понятие «гильдия» и «трофическая группировка» оказываются синонимами.

4.2.2. Видовое разнообразие стационарных биоценозов

С каждым из n видов биоценоза сопоставим некоторый показатель значимости p_i (i = 1,2,…,n), рассматриваемый как мера относительного доминирования или участия данного вида в сообществе или в его функционировании. В качестве показателя значимости вида может использоваться процентная доля вида в первичной продукции сообщества или доля дыхания данного вида в общем дыхании видов биоценоза. При рассмотрении сообществ, составленных из особей сравнимого размера, биомассы и метаболизма, в качестве показателя значимости (доминирования) допустимо использовать просто индекс относительного обилия, иногда выражаемый в процентах.

.

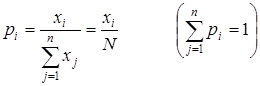Из общего числа видов сообщества в целом обычно лишь немногие бывают доминирующими, то есть имеют значительную численность (большую биомассу, продуктивность и т.п.); большая же часть относится к редким видам. Правда, иногда доминантные виды отсутствуют, а имеется большое число видов со средним значением показателя значимости.

Видовое разнообразие слагается из двух компонентов:

1) видового богатства, которое характеризуется общим числом имеющихся видов 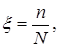где ;

2) выравненности, основанной на относительном обилии или другом показателе значимости вида и положении его в структуре доминирования.

Видовое разнообразие увеличивается при увеличении размеров площади и при продвижении от высоких широт к экватору. В сообществах же, подвергающихся стрессовым воздействиям, видовое разнообразие невелико; но, кроме того, оно может снижаться в результате конкуренции в старых сообществах, существующих в стабильной физической среде.

Большую роль играют два других типа разнообразия:

1) структурное разнообразие;

2) генетическое разнообразие, то есть поддержание генотипических гетерозиготности (присутствие в хромосоме доминантных и рецессивных признаков), полиморфизма и другой генотипической изменчивости, которая вызвана адаптационной необходимостью в природных популяциях.

Уменьшение видового и генотипического разнообразия, происходящее вследствие деятельности человека, ставит на грань риска возможность будущих адаптаций как в природных экосистемах, так и в агроэкосистемах.

Для изучения видового разнообразия принято строить кривую относительного доминирования-разнообразия, введенную в рассмотрение Уиттэкером (1965): по оси x (абсцисс) отложена ранжированная последовательность номеров видов i от наиболее значимого до наименее значимого, а по оси y (ординат) – величина показателя зависимости p_i соответствующего вида, обычно в логарифмическом масштабе.

Выделяют три основных типа поведения кривой относительного доминирования, соответствующих различным типам взаимодействий между видами в сообществе.

Кривая 1 отвечает ситуации, когда члены сообщества находятся в сильной зависимости от некоторого ресурса, распределенного вдоль одномерного континуума, причем имеет место случайное, но без пересечений распределение частных ниш видов вдоль координатной оси данного ресурса (так называемая модель «разломанного стержня» Р. Мак-Артура). Показатель значимости в этом случае ведет себя в соответствии с формулой

.

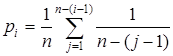Подобный тип рангового распределения наиболее часто встречается в немногочисленных по числу видов группировках таксономически близких животных в четко ограниченных однородных биоценозах, как, например, группировка птиц, гнездящихся на ограниченном участке леса, а также справедлива для высших животных с активной конкуренцией, устойчивой численностью и высокой продолжительностью жизни.

Кривая 2, представляющая собой прямую, изображает случай так называемого «геометрического» распределения и соответствует следующей схеме относительного доминирования: первый вид занимает половину доступного пространства ниш, второй – половину оставшегося пространства (25% исходного) и т.д. В более общем случае существует фиксированное число с (0 £ с £ 1), такое, что

p₁ = cp, где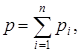

p₂ = c(p - p₁) = c(1 - c)p , p₃ = c(p - p₁ - p₂) = c(1 - c)² p

……………………

p_i = c(1 - c)^i-1 p

или в логарифмическом виде

log p_i = (i - 1) log (1 - c) + log c + log p ,

откуда видно, что величина p_i как функция ранга i изображается на полулогарифмической шкале прямой линией с угловым коэффициентом log (1 - c). Геометрическое распределение относительного доминирования обнаруживается в группировках, состоящих из небольшого числа видов, которые состоят в жесткой конкуренции за ограниченные ресурсы, нередко в суровых условиях внешней среды. Получаемую круто падающую прямую 2 можно рассматривать в качестве альтернативы для относительно пологой кривой 1, соответствующей распределению Мак-Артура.

Эти две кривые представляют крайние случаи, обычно же распределение в природе имеет вид промежуточной S-образной кривой 3, что указывает на более сложный характер дифференциации и перекрывания ниш. Распределение, изображаемое кривой 3, называется логнормальным. Это связано с тем, что гистограмма распределения логарифмов ln p_i по октавам (диапазонам значений p_i, отличающихся на границах в 2 раза) приближается по форме к нормальному распределению. Значения n_j (число точек, попавших в данную октаву j) для различных октав с номерами j = …,-2,-1,0,1,2,… (где 0 – октава с наибольшим числом точек) могут быть аппроксимированы выражением

,

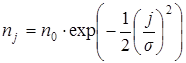где s – мера рассеяния относительно модального класса j=0, которая для большинства анализируемых видовых группировок находится в пределах 1£s£5.

Логнормальное распределение относительного доминирования характерно для сообществ с высокой видовой насыщенностью, в условиях, когда «успех» того или иного вида определяется большим числом относительно независимых и однородных по силе влияния факторов. В этом случае ниши многомерны и перекрываются.

В общем расположение видов по степени значимости кривая доминирования не только точно отражает богатство и относительное обилие видов как компонентов видового разнообразия, но и объясняет, каким образом подразделяется пространство ниш. Чем выше кривая и чем более она уплощена, тем больше при данном числе видов общее разнообразие. Чем круче идет кривая, тем меньше общее разнообразие и сильнее доминирование одного или нескольких видов. В стрессовых ситуациях независимо от того, вызваны ли они естественными причинами (погодными условиями) или антропогенным воздействием, кривая становится более крутой. Таким образом, кривую доминирования можно использовать для оценки влияния нарушений на видовую структуру.

Кроме видового богатства и типа рангового распределения для характеристики сообществ используется так называемый показатель (индекс) разнообразия, который количественно отражает не только общее число видов, но и особенности количественного состава сообществ. К наиболее часто употребимым относят показатель разнообразия по Симпсону

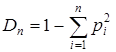
показатель разнообразия по Шеннону

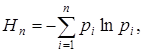
и показатель выравненности Пиелу

E = H / ln n .

Оба показателя разнообразия обладают тем свойством, что они принимают максимальное значение при равенстве долей всех видов в сообществе, то есть при p₁ = p₂ = … = p_n = 1/n ( )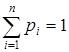

.

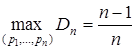
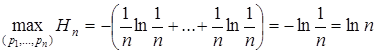С другой стороны, когда доля какого-нибудь одного вида, например i-го, стремится к 1, а всех остальных – к нулю, оба показателя также стремятся к нулю:

,

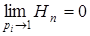
Из двух обобщенных индексов показатель Симпсона придает обычным видам больший вес, поскольку при возведении в квадрат малых значений p_i получаются очень малые величины. Индекс Шеннона придает больший вес редким видам. Так как индекс Шеннона заимствован из теории информации и представляет собой формализацию, которая широко используется при оценке сложности и содержания информации в любых типах систем, он лучше всего подходит для целей сравнения в тех случаях, когда нас не интересуют компоненты разнообразия по отдельности.

При построении Ю. Одумом гистограммы для показателя разнообразия Симпсона для разных биоценозов выяснилось, что полученная гистограмма оказалась бимодальной: выделилась одна большая группа биоценозов с низким разнообразием (0.05 – 0.2) и другая большая группа со сравнительно высоким разнообразием (0.7 – 0.85). Во всей выборке не оказалось биоценоза с примерно равными значениями показателей относительного доминирования (p₁ = … = p_n = 1/n), когда индекс разнообразия приближается к своему максимальному значению, то есть к 1.

В группу с низким биотическим разнообразием попали: 1) экосистемы, находящиеся в состоянии стресса под действием внешних сил или притоков вещества или энергии, как в случае загрязненных рек или заливов, или экосистемы, активно регулируемые человеком, как посевы сельскохозяйственных культур или лесные плантации; 2) экосистемы, постоянно получающие большие количества высококачественной энергии или полезных веществ. Биоценозов со средним (около 0.5) разнообразием оказалось сравнительно мало.

Группы с высоким разнообразием образованы многими естественными экосистемами, не получающими извне концентрированной энергии или биогенных материалов и живущими только за счет солнца, например, степи, леса и большие озера.

Эти данные свидетельствуют о том, что видовое богатство и разнообразие биоценозов формируется в результате приспособления к силе и количественному составу приходящего энергетического потока. «Стратегия» природы состоит в увеличении разнообразия, но только до пределов, пока это не приводит к снижению эффективности использования ресурсов биоценоза. Следовательно, существует некоторый оптимум разнообразия, определяемый эффективностью экосистемы как энергетической машины. При больших внешних энергетических субсидиях в экосистеме эффективна простая, но специализированная структура с низким видовым разнообразием, способная использовать эти благоприятные условия более эффективно, чем менее специализированная совокупность видов.

В условиях ограниченного энергетического притока более выгодным для поддержания стационарного состояния экосистемы представляется высокий уровень разнообразия: порядка 0.7÷0.8. В этом случае достигается определенная надежность использования дефицитного источника энергии благодаря наличию многих альтернативных путей ее обесценивания.

4.2.3. Динамика популяций в биоценозах

Популяции в биоценозах обычно находятся в тесном взаимодействии. Одна популяция часто влияет на скорость роста или смертность другой. Так, члены одной популяции могут поедать членов другой популяции, конкурировать с ними за пищу, выделять вредные подавляющие развитие вещества или взаимодействовать с ними другим способом. Точно так же популяции могут быть полезными друг для друга, причем польза в одних случаях оказывается обоюдной, а в других – односторонней.

Для выяснения действий различных факторов в сложных природных ситуациях полезно пользоваться «моделями» в форме уравнений. Построение большинства моделей взаимодействия в биологических сообществах опирается на описание взаимодействия с помощью системы дифференциальных уравнений относительно численности видов x_i(t). В предположении постоянства внешних и внутренних экологических факторов {v₁,v₂,…,v_m} = const, а также без учета возрастной структуры популяций, динамику биоценоза, вызываемую межвидовыми взаимодействиями, можно описать с помощью системы дифференциальных уравнений вида

.

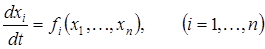где функции f_i(….) , стоящие в правых частях, представляют собой частные функции отклика абсолютных скоростей изменения плотности популяций на значения самих этих плотностей, равные разности абсолютных скоростей размножения и гибели при фиксированных значениях экологических факторов:

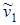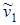f_i(x_1,…,x_n) = B_i( ,…, , x_1,…,x_n) – D_i( ,…, , x_1,…,x_n).

То есть функции f_i(…) описывают скорость изменения численности популяций в зависимости от структуры видовых взаимодействий.

Данная модель воспроизводит динамику видового состава биоценоза под влиянием одних биотических взаимодействий между популяциями, каждая из которых описывается на уровне полного внутрипопуляционного агрегирования, поскольку функции f_i(…) зависят только от плотности популяций. Модели подобного типа называются биоценотическими моделями динамики популяций.

Предположим, что функции f_i(…) не зависят явным образом от времени и рассматриваемая система дифференциальных уравнений является изолированной. Тогда из равенства x_i = 0 вытекает f_i(x₁, x_2,…, x_i-1, 0_, x_i+1,…,x_n) = 0 и f_i(…)представимы в виде:

f_i(x_1, x_{2, …,}x_n) = x_i r_i(x_1, x_{2, …,}x_n),

где r_i(…) – удельная скорость изменения плотности популяции i-го вида (или обобщённый коэффициент прироста).

В простейшем случае в некоторой рассматриваемой области изменения плотностей популяций X_i= {x_i^s£x_i(t)£x_i^e, i =1,.., n} удельные скорости изменения каждой популяции достаточно точно аппроксимируются линейными функциями плотностей

r_i (x_1, x_{2, …,}x_n) = r_i^m - ,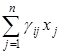

что приводит к системе уравнений

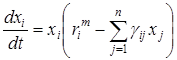, (i= 1, 2, …, n).

Модели такого типа в литературе по экологии принято называть вольтерровскими. Здесь - скорость естественного прироста в отсутствии остальных видов, то есть биотический потенциал i-го вида; 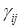- показатели внутривидового взаимодействия, они отражают характер взаимодействия видов. Матрицу

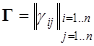
обычно называют матрицей сообществаили матрицей взаимодействия. Коэффициенты 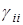матрицы Гвлияют на коэффициент естественного прироста численности i-го вида при отсутствии других видов. Если 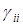>0, то говорят о наличии внутривидовой конкуренции или самолимитирования по численности i-го вида. Как видно, для случая одного вида данная система преобразуется к виду логистического уравнения, описывающего динамику популяций в среде с ограниченными ресурсами.

Влияние j-го вида на i-й вид задано с помощью произведения в соответствии с гипотезой «встреч и эквивалентов». Число встреч особей видов i и j за время dt равно 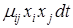. В результате этих встреч происходит сокращение численности вида i на величину 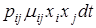, где 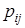указывает на долю особей вида i, которые истребляются при встрече (0£ 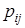£1). В тоже время число особей вида j возрастает на величину 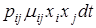с некоторым коэффициентом пропорциональности, называемым эквивалентом. Таким образом, происходит немедленное преобразование биомассы вида i в биомассу вида j.

Представляет интерес нахождение стационарного состояния вольтерровской системы, то есть такой комбинации численностей популяций , при которых производные 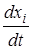(скорости) обращаются в нуль. Положение равновесия вольтерровской системы должно удовлетворять системе уравнений

=0 (i= 1, 2, …, n).

Так как нас интересуют только положительные и ненулевые решения, то есть , то искомое положение равновесия является решением системы уравнений

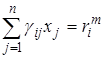(i= 1, 2, …, n).

или в матричной форме

ГХ= R,

где R = ,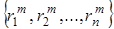

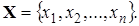
Рассмотрим проблему устойчивости получаемого решения вольтерровской системы. При исследовании таких систем Вито Вольтерра рассматривал два подкласса таких систем – консервативные и диссипативные.

Для указанного рассмотрения проанализируем, как изменяется общая масса биоценоза

,

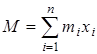где 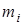– среднее значение биомассы особей вида i. На траекториях системы, задающей поведение скорости изменения численностей популяций 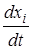, общая биомасса сообщества будет изменяться в соответствии с уравнением

.

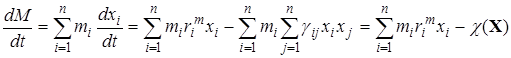Если квадратичная форма 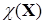такова, что

,

то вольтерровская система называется консервативной. Если же квадратичная форма 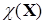положительно определена, система называется диссипативной.

Таким образом, для консервативных систем характерен неограниченный рост общей биомассы сообщества. В диссипативной системе рост общей биомассы замедляется вследcтвии влияния взаимодействия видов.

Для консервативной системы должно выполнятся:

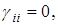
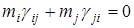, i, j = 1,2,…,n .

Таким образом, коэффициенты 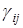и 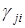имеют противоположные знаки или одновременно равны нулю.

Рассмотрим функцию Ляпунова вольтерровской системы

и вычислим производную этой функции вдоль траектории вольтерровской системы, представленной в соответствии с 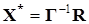в следующем виде

.

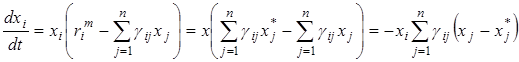Имеем

или

.

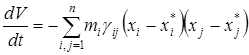Если система консервативна, то это выражение тождественно равно нулю. Функция V(X) является функцией Ляпунова для системы = и достигает минимального значения в точке 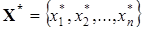. Поскольку производная функции V(X) тождественно равно нулю для всех 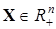, то положение равновесия X^* устойчиво.

Для консервативных систем в случае невырождённости матрицы Г и при чётном n первый интеграл имеет вид

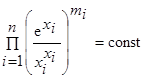
Отсюда следует, что при X^* > 0 численности всех видов ограничены сверху и снизу положительными константами, и если X₀ ≠ X^*, то по крайней мере один вид имеет незатухающие колебания численности. Причём средние значения численности

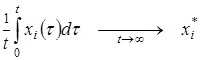
Это свойство называется законом асимптотических средних.

В диссипативных системах квадратичная форма c(X) положительно определена. Отсюда следует, что все g_ii > 0, то есть все виды должны обладать самолимитированием. Это говорит о том, что классы консервативных и диссипативных систем не пресекаются. Ещё одним необходимым условием диссипативности является неравенство нулю определителя матрицы Г, откуда сразу следует единственность решения системы ГХ=R. И, наконец, последнее необходимое условие состоит в том, что все главные миноры матрицы Г положительны.

Если Х^* > 0, то для диссипативных систем первый интеграл системы имеет вид

,

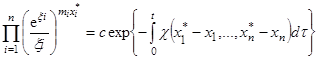где x_i = x_i / x_i^*, c > 0. Поскольку квадратичная форма c положительно определена, то, как показал В. Вольтерра, Х(t) ® Х^* при t®¥ при любих начальных значениях Х₀ = Х(0) Î Rⁿ₊ .

Кроме того, на траекториях диссипативной системы получаем dV/dt £ 0 для всех Х(t) Î Rⁿ₊ , причём равенство dV/dt = 0 выполняется только при Х(t) = Х^*. Это означает, что Х(t) ® Х* при t ® ¥, и положение равновесия асимптотически устойчиво при любых начальных данных из Rⁿ₊ , то есть областью асимптотической устойчивости является весь неотрицательный ортант.

Для решения вопроса о локальной устойчивости получаемого стационарного состояния Х^*=Г^-1R необходимо установить вид структурной матрицы системы Лотки-Вольтерра в точке Х^*. Элемент (ij) этой матрицы определяют влияние j-го вида на динамику i-го вида