Актуальность изучения экологии 10 страница
Перепишем коэффициенты конкуренции в виде 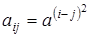 ,
, 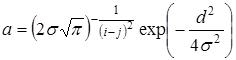 . Тогда получим матрицу конкуренции
. Тогда получим матрицу конкуренции
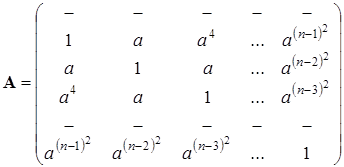
Величиной 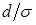 обычно характеризуют плотность видовой упаковки сообщества или меру близости экологических ниш. Диссипативность матрицы
обычно характеризуют плотность видовой упаковки сообщества или меру близости экологических ниш. Диссипативность матрицы 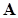 сохраняется при всех даже достаточно малых значениях
сохраняется при всех даже достаточно малых значениях 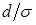 . Поэтому положительное положение равновесия будет асимптотически устойчиво при видовой упаковке любой плотности.
. Поэтому положительное положение равновесия будет асимптотически устойчиво при видовой упаковке любой плотности.
4.2.10. Отношения типа «жертва-эксплуататор» (+ , -)
К этой категории биотических отношений принадлежат любые отношения между двумя видами, при которых увеличение плотности популяции первого («жертвы») влечет за собой увеличение скорости роста популяции второго («эксплуататора»), тогда как увеличение плотности популяции второго вызывает уменьшение скорости роста популяции первого вида.
Наиболее важными примерами такого рода являются отношения:
1) растения и травоядного животного;
2) жертвы и хищника (в узком смысле этих терминов);
3) хозяина и паразита.
Из наблюдений над природными и антропогенными экосистемами известно, что при взаимодействиях типа «жертва-эксплуататор» возможны следующие основные «сценарии», изображающиеся характерными типами фазовых портретов на плоскости (x1, x2), где x1 – плотность популяции жертвы, а x2 – эксплуататора:
1. «Ускользание» жертвы от неэффективного эксплуататора.
 |
Вид-эксплуататор не способен прокормиться за счет данной жертвы и со временем вымирает (
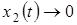 при
при 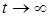 ), а сама жертва после некоторого переходного процесса достигает определенной стационарной численности
), а сама жертва после некоторого переходного процесса достигает определенной стационарной численности 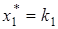 . Такое развитие событий нередко бывает при попытках применения «биологического» метода борьбы с вредителем путем введения в рассматриваемую экосистему хищника или паразита, уничтожающего вредный вид.
. Такое развитие событий нередко бывает при попытках применения «биологического» метода борьбы с вредителем путем введения в рассматриваемую экосистему хищника или паразита, уничтожающего вредный вид.
2. Эксплуататор полностью истребляет жертву, после чего сам погибает от голода. Вид-эксплуататор слишком эффективен в поисках жертвы, прожорлив и быстро размножается, в результате чего он полностью истребляет жертву, после чего и сам погибает от голода. Например, травоядные на островах, лишенных хищников, выедают всю растительность и вымирают (см. рис. ниже).
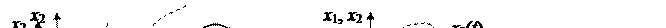 |
3. Существование «жестко» устойчивого стационарного состояния. Из любого начального состояния
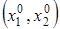 система жестко (то есть без колебаний) переходит в стационарную точку
система жестко (то есть без колебаний) переходит в стационарную точку 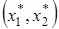 . Этот вариант соответствует ситуации, когда эксплуататор достаточно эффективен и может быстро снижать численность жертвы до низкого стационарного уровня
. Этот вариант соответствует ситуации, когда эксплуататор достаточно эффективен и может быстро снижать численность жертвы до низкого стационарного уровня 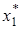 , вблизи которого начинают действовать некоторые механизмы, препятствующие полному истреблению жертвы, как, например, наличие укрытий, трудность обнаружения редких экземпляров, наличие иммунной прослойки и резкое ограничение числа контактов в изреженной популяции жертвы.
, вблизи которого начинают действовать некоторые механизмы, препятствующие полному истреблению жертвы, как, например, наличие укрытий, трудность обнаружения редких экземпляров, наличие иммунной прослойки и резкое ограничение числа контактов в изреженной популяции жертвы.
4. Наличие «мягко» устойчивого стационарного состояния, переход к которому осуществляется через затухающие колебания. Из любого начального состояния 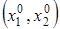 после переходного процесса с затухающими колебаниями система стремится к своему исходному состоянию
после переходного процесса с затухающими колебаниями система стремится к своему исходному состоянию 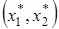 , в котором жертва и эксплуататор могут устойчиво существовать неограниченно долго. Такой режим весьма характерен для взаимодействия растений и копытных растительноядных.
, в котором жертва и эксплуататор могут устойчиво существовать неограниченно долго. Такой режим весьма характерен для взаимодействия растений и копытных растительноядных.
 |
5. Существование устойчивого колебательного режима типа «предельного цикла». Из любого начального состояния
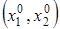 траектория системы стремится к единственной замкнутой траектории, движение по которой осуществляется с периодом T, то есть в системе возникают автоколебания численностей популяций. Наличие периодичных колебаний численностей видов, необъяснимых колебаниями внешних климатических факторов, всегда ставила в тупик биологов. И лишь исследования Лотки-Вольтерра позволило объяснить эти колебания на основе математического моделирования системы «жертва-хищник».
траектория системы стремится к единственной замкнутой траектории, движение по которой осуществляется с периодом T, то есть в системе возникают автоколебания численностей популяций. Наличие периодичных колебаний численностей видов, необъяснимых колебаниями внешних климатических факторов, всегда ставила в тупик биологов. И лишь исследования Лотки-Вольтерра позволило объяснить эти колебания на основе математического моделирования системы «жертва-хищник».
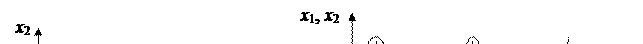 |
В 1936 г. А. Н. Колмогоров предложил использовать для описания динамики системы «жертва-хищник» следующую систему уравнений
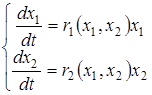 , (К.1)
, (К.1)
где 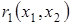 и
и 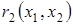 - удельные скорости роста жертвы и эксплуататора. Методами качественной теории дифференциальных уравнений удалось доказать, что если функции
- удельные скорости роста жертвы и эксплуататора. Методами качественной теории дифференциальных уравнений удалось доказать, что если функции 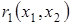 и
и 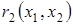 удовлетворяют ниже перечисленным условиям.
удовлетворяют ниже перечисленным условиям.
1) 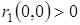 – численность жертв возрастает, когда оба вида малочисленны;
– численность жертв возрастает, когда оба вида малочисленны;
2) 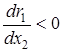 – удельная скорость прироста популяции жертвы является убывающей функцией численности эксплуататора;
– удельная скорость прироста популяции жертвы является убывающей функцией численности эксплуататора;
3) 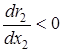 – размножение эксплуататоров замедляется с ростом их численности;
– размножение эксплуататоров замедляется с ростом их численности;
4) 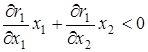 ,
, 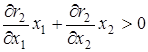 – при постоянном отношении численностей жертв и эксплуататоров размножение жертв замедляется с увеличением числа эксплуататоров, а размножение эксплуататоров стимулируется увеличением числа жертв;
– при постоянном отношении численностей жертв и эксплуататоров размножение жертв замедляется с увеличением числа эксплуататоров, а размножение эксплуататоров стимулируется увеличением числа жертв;
5) 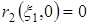 – существует критическая для эксплуататора численность жертвы
– существует критическая для эксплуататора численность жертвы 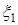 , ниже которой он не может размножаться;
, ниже которой он не может размножаться;
6) 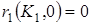 ,
, 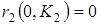 – существуют предельно высокие численности жертвы
– существуют предельно высокие численности жертвы 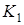 и эксплуататора
и эксплуататора 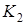 , после достижения которых рост жертвы прекращается.
, после достижения которых рост жертвы прекращается.
 |
В этом случае необходимым и достаточным условием существования в модели (К.1) устойчивого стационарного состояния (сценарии 3 и 4) или устойчивого колебательного режима (сценарий 5) будет выполнение неравенства
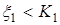 .
.
При этом когда 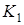 – емкость среды для жертвы, намного превосходит плотность популяции жертвы в стационарном состоянии
– емкость среды для жертвы, намного превосходит плотность популяции жертвы в стационарном состоянии 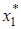 , то можно ожидать наличия устойчивого предельного цикла
, то можно ожидать наличия устойчивого предельного цикла 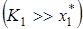 . Если же
. Если же 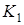 и
и 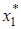 различаются не очень сильно, то точка
различаются не очень сильно, то точка 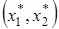 будет устойчивым стационарным состоянием. В частности, достаточным условием существования предельного цикла является не отрицательность действительной части характеристического уравнения (
будет устойчивым стационарным состоянием. В частности, достаточным условием существования предельного цикла является не отрицательность действительной части характеристического уравнения ( 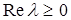 ):
):
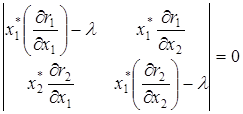 ,
,
где все частные производные вычислены в стационарной точке (х1*, х2*) .
Более содержательным является анализ менее общей модели, предложенной также Колмогоровым:
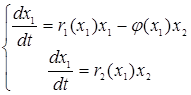 ,
,
где r1(x1) = b1(x1) - d1(x1) – удельная скорость прироста жертвы в отсутствии эксплуататоров, r2(x1) = qj(x1) - d2(x1) – удельная скорость прироста эксплуататора, j(x1) – функция выедания (трофическая функция).
Колмогоров показал, что его вторая система имеет определенные решения, если функции r1(x1), r2(x1) и j(x1) удовлетворяют условиям, приведенным ниже:
1) 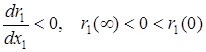 – внутривидовая конкуренция в популяции жертвы усиливается с ростом численности и препятствует ее чрезмерному увеличению, при этом r1(x) обращается в нуль при x1= K1, которое является верхней границей численности популяции жертвы в отсутствии хищников;
– внутривидовая конкуренция в популяции жертвы усиливается с ростом численности и препятствует ее чрезмерному увеличению, при этом r1(x) обращается в нуль при x1= K1, которое является верхней границей численности популяции жертвы в отсутствии хищников;
2) 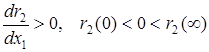 – в отсутствие жертвы эксплуататор погибает, а увеличение ее численности ускоряет прирост численности эксплуататора;
– в отсутствие жертвы эксплуататор погибает, а увеличение ее численности ускоряет прирост численности эксплуататора;
3) j(x1) > 0 при x1 > 0 – при наличии жертвы эксплуататор всегда способен ее обнаружить и только при x1 = 0 функция выедания обращается в нуль.
В этом случае вторая система Колмогорова может иметь только решения, описываемые сценариями (1), (3), (4) и (5) в зависимости от свойств функций r1(x1), r2(x1) и j(x1).
Стационарными точками системы являются (К1,0),где К1 определяется из уравнения r1(К1) = 0, и точка (x1*,x2*), которая является решением системы уравнений:
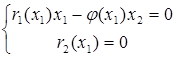 или
или 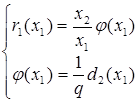
Поведение решения второй системы Колмогорова существенным образом зависит от вида функции выедания j(х1), поэтому имеется большое число разнообразных моделей, отличающихся в первую очередь видом функции выедания. Рассмотрим простейшую модель функции выедания в виде линейной функции
j(х1) = g 12 х1,
где g12 = const > 0. Если принять рождаемость жертвы, смертность жертвы и эксплуататора – постоянной (b1 = const > 0, d1 = const > 0, d2 = const > 0), то получаем так называемую модель Лотки-Вольтерра системы “ хищник-жертва”:
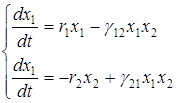 ,
,
где r1 = b1 - d1 , r2 = d2 и g21 = qg12.
Умножим первое уравнение на g21 и сложим со вторым, умноженным на g12:
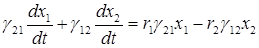 .
.
Далее умножим первое уравнение на r2/x1 и сложим со вторым, умноженным на r1/x2:
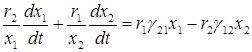 .
.
Из двух полученных уравнений получаем
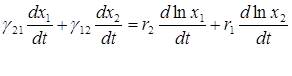 .
.
Интегрируя, получаем
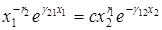 ,
,
где 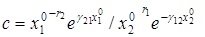 .
.
Это уравнение описывает семейство замкнутых кривых с центром в точке:
x1* = r2/g21, x2* = r1/g12 .
Изучая поведение этих кривых, В.Вольтерра пришел к важному выводу о периодичности колебаний численности популяций и об устойчивости положения равновесия (х1*, х2*), которое является средним значением (х1, х2) по периоду колебаний Т. Действительно, перепишем рассматриваемую систему в виде
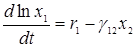 ,
, 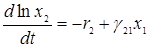 ,
,
и проинтегрируем обе части уравнений по интервалу времени, равному одному периоду колебаний, и с учетом периодичности получим
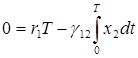 ,
, 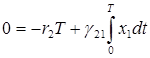 .
.




|
Окончательно имеем
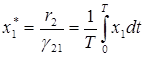 ,
, 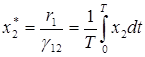 .
.
Эти соотношения выражают закон сохранения средних значений: средние значения численностей хищников и жертв не зависят от начальных условий и равны численности в положении равновесия.
Если единовременно отстрелять часть животных, например, хищников, произойдет переход с траектории 1 на меньшую траекторию 2. При этом среднее число хищников не изменится, а лишь уменьшится колебаний численностей хищника и жертвы.
Если в системе хищник-жертва происходит искусственное уничтожение особей обоих видов, пропорционально их численности с коэффициентами пропорциональности a1 и a2, то система уравнений примет вид
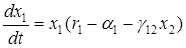
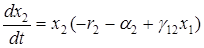
Среднее значение численностей в этом случае составят
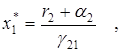
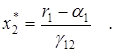
То есть, если a1 < r1 , то средняя численность популяций жертвы возрастает, а хищника – убывает. Это так называемый закон изменения средних. Если a1 > r1, то оба вида исчезают.
Если в модели Вольтерра учесть саморегулирование численности жертвы, то получим модифицированную систему Лотки-Вольтерра
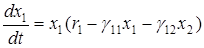 ,
, 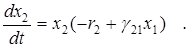
Фазовый портрет этой системы соответствует сценарию 4 (переход в стационарное состояние через затухающие колебания), введение внутривидовой конкуренции среди жертв привело к стабилизации системы. Координаты стационарной точки равны:
x1*=r2/g21 , x2*=r1/g12 -g11r2/g12g21 .
4.2.11. Управление численностью видов в экосистемах
Рассмотрим задачу управления вольтерровской системой
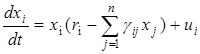 ,
,
где вектор управления U= (u1, u2,…, un) выбирается из некоторого множества допустимых управлений U. Предположим, что в этой системе при Uº 0 существует устойчивое состояние равновесия Х*. Рассмотрим задачу: найти такой вектор управления u Î U, чтобы система получила новое устойчивое положение равновесия 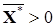 . Таким образом, поставлена задача перевода экосистемы на новый режим, при котором поддерживалась бы заданная численность популяций.
. Таким образом, поставлена задача перевода экосистемы на новый режим, при котором поддерживалась бы заданная численность популяций.
Выберем в качестве допустимых управлений векторы вида
U= CX,
где матрица С= diag{ci} . Перепишем рассматриваемую систему в виде
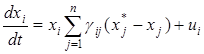
и подставим вместо управления ui его выражение через диагональную матрицу
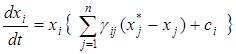 .
.
Найдем теперь сi , исходя из условия, что эта система имеет положение равновесия 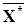 . Для этого необходимо, чтобы при X=
. Для этого необходимо, чтобы при X= 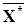 выражение в скобках равнялось нулю. Отсюда получаем
выражение в скобках равнялось нулю. Отсюда получаем
ci = 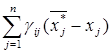 .
.
Таким образом, если в рассматриваемой системе управление выбирается в виде U= CX с указанными коэффициентами сi , то у нее появляется новое положение равновесия 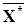 , причем устойчивое, если было устойчивым положение равновесия
, причем устойчивое, если было устойчивым положение равновесия 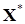 , поскольку на коэффициенты матрицы сообщества управление не оказывает влияния.
, поскольку на коэффициенты матрицы сообщества управление не оказывает влияния.
5. Развитие и эволюция экосистем
5.1. СТРАТЕГИЯ РАЗВИТИЯ ЭКОСИСТЕМЫ
5.1.1. Экологическая сукцессия
Несмотря на то, что естественная экосистема находиться в состоянии подвижно-стабильного равновесия, она испытывает медленные, но постоянные изменения во времени, имеющие последовательный характер. Эти изменения в первую очередь касаются биоты, то есть входящего в состав биогеоценоза живого населения.
Такую последовательную смену одного биоценоза (биоты) другим называют сукцессией. Простейший пример сукцессии – последовательное освоение грибами, бактериями, беспозвоночными упавшего в лесу дерева.
Таким образом, развитие экосистемы, более известной под названием экологической сукцессии, состоит в изменении во времени видовой структуры и биоценотических процессов.
Сукцессия происходит в большей степени за счет конкуренции и других взаимодействий между популяциями, составляющими биоценоз, в меньшей степени – за счет изменений сообществом физической среды. Таким образом, сукцессия контролируется сообществом, несмотря на то, что физическая среда определяет характер и скорость изменения, а часто ограничивает пределы развития. В отсутствие внешних нарушающих процессов сукцессия представляет направленный и, следовательно, предсказуемый процесс. Одум в 1955 г., опираясь на сформулированный Лоткой «закон максимума энергии в биологических системах», впервые указал на то, что сукцессия связана с фундаментальным сдвигом потока энергии в сторону увеличения количества энергии, направленной на поддержание (дыхание) системы, по мере того, как накапливается биомасса и органическое вещество.
Если сукцессионные изменения определяются преимущественно внутренними взаимодействиями, то говорят об аутогенной (то есть самопорождающейся) сукцессии. Если же на изменения регулярно воздействуют или контролируют их внешние силы среды на входе (например, штормы и пожары), то такую сукцессию называют аллогенной (порожденной извне).
Последовательность сообществ, сменяющих друг друга в данном пространстве, называют серией; относительно недолговечные переходные сообщества называют по-разному: сериальными стадиями, или стадиями развития, или пионерскими стадиями. Терминальная стабилизированная экосистема известна под названием климакса, который теоретически должен быть постоянным во времени и существовать до тех пор, пока его не нарушат сильные внешние возмущения.
Сукцессия, начинающаяся с состояния P > R, – это автотрофная сукцессия; напротив, если сукцессия начинается с состояния P < R, то это гетеротрофная сукцессия.
Сукцессия, начинающаяся на участке, который прежде не был занят (на потоке застывшей лавы, например), называется первичной сукцессией, тогда как сукцессия, начинающаяся на площади, с которой удалено прежнее сообщество (например, на лесной вырубке или заброшенном поле), называется вторичной сукцессией. Различают сукцессии зоогенные (вызванные необычно сильным воздействием животных), фитогенные, антропогенные, а также катастрофические (следствие пожаров, ветровала, загрязнение воды или атмосферы и т.д.).
5.1.2. Тенденции изменения основных характеристик экосистем
Биоэнергетика развития экосистемы. Аутогенная сукцессия при заселении новых территорий (возникших в результате извержения вулканов, строительства новых водохранилищ) обычно начинается с несбалансированного сообщества. Метаболизм в таком сообществе характеризуется тем, что валовая продукция (P) либо больше, либо меньше дыхания (R), в зависимости от того: является ли сукцессия автотрофной (P > R) или гетеротрофной (P < R); и процесс направлен в сторону более сбалансированного состояния, когда P = R. Иными словами, в зрелой, или климаксной, экосистеме наблюдается тенденция к равновесию между связанной энергией и энергией, затрачиваемой на поддержание биомассы (то есть суммарным дыханием сообщества). Таким образом, отношение P/R является функциональным показателем относительной зрелости экосистемы.
Пока P больше R, в системе будут накапливаться органическое вещество и биомасса (B), в результате чего отношение B/P будет увеличиваться. Отношение биомассы к продукции возрастает в течение сукцессии до тех пор, пока не произойдет стабилизация экосистемы, в которой на единицу доступного потока энергии будет приходиться максимум биомассы и симбиотических связей между организмами (или высокое содержание информации). Итак, B/P → max в климаксных системах. Как следствие этого, чистая продукция сообщества велика на ранних стадиях и мала в зрелой системе.
Круговорот биогенных элементов. Важной тенденции в развитии сукцессии являются увеличение времени оборота и повышение способности к сохранению и регенерации веществ. Все это приводит к замыканию или «уплотнению» биогеохимических циклов основных биогенных элементов, таких, как азот, фосфор и кальций.
Индекс возобновления (CI), равный отношению регенерированной части (то есть используемой неоднократно) на входе к выходу, устойчиво возрастает по мере созревания системы. Биогены удерживаются более долгое время и используются повторно, при этом необходимость их притока уменьшается. Таким образом, в процессе развития экосистемы возрастает запас и степень возобновления биогенных элементов, в результате необходимый уровень поступления этих элементов на вход для поддержания единицы биомассы снижается.
В ходе сукцессии происходит смена источника азота с нитрата на аммоний. При переходе с нитрата на аммоний уменьшается количество энергии, расходуемое на регенерацию азота, и возрастает, следовательно, эффективность использования энергии.
Изменение видовой структуры экосистемы. Характерная черта большинства сукцессионных серий – это более или менее непрерывная смена видового состава экосистемы во времени, называемая часто «флористической» и «фаунистической» эстафетой.
На вырубке или заброшенной пашне в определенной последовательности появляются сначала травянистые растения, далее – в результате налета семян – всходы деревьев и кустарников, причем обычно сначала развиваются светолюбивые и относительно быстрорастущие лиственные породы, и лишь по прошествии определенного времени под пологом лиственных начинают расти хвойные. Пример такой сукцессии – смена березы елью, ели – сосною, осины – дубом и т.п.
Наиболее резко меняется видовой состав сообщества при смене доминирующих жизненных форм растений (травы – кустарники – сосны – лиственные породы). Не один вид растений или животных не может процветать на протяжении всей сукцессии. Максимумы разных видов приходятся на разные точки временной шкалы.
При сукцессии изменяется качественный состав видов. На ранних стадиях сукцессии, когда плотность населения мала, преобладает r-отбор, то есть успешно вселяются виды с высокой скоростью размножения и роста, так называемые r-стратеги, для которых характерен экспоненциальный рост их численности. При равновесной плотности, характерной для поздних стадий сукцессии, давление отбора благоприятствует К-стратегам, то есть видам с низким потенциалом роста, но более высокой способностью к выживанию в условиях конкуренции, и r-стратеги в широких масштабах замещаются К-стратегами.
Происходящий при сукцессии переход от количества продукции к качеству сопровождается генетическими изменениями, охватывающими всю биоту, которые проявляются в увеличении размеров организмов и в усложнении и удлинении их жизненных циклов. Мелкие организмы обладают селективным преимуществом в среде, богатой биогенами и компонентами минерального питания. Однако по мере развития экосистемы неорганические биогенные элементы оказываются все более и более связанными в биомассе, так что селективное преимущество переходит к более крупным организмам, способность к запасанию веществ у которых выше и жизненные циклы сложней. Благодаря этим свойствам они адаптированы к использованию сезонных или периодических поступлений биогенов или других ресурсов.
По мере развития сукцессии возрастает видовое богатство сообщества как компонент разнообразия и возрастает выравненность как компонент разнообразия. Характер изменения видового разнообразия – непрерывный рост или прохождение пика в промежуточной стадии – зависит от соотношения двух процессов, а именно от возрастания числа потенциальных ниш в результате увеличения биомассы, стратифицированности и других последствий биологической организации, и от противоположных эффектов увеличения размеров организмов и конкурентного исключения среди хорошо адаптированных долго живущих доминантов, которые снижают видовое разнообразие.
Дата добавления: 2017-09-19; просмотров: 603;