Оценка безрисковой ставки доходности

Начальный шаг оценки стоимости капитала по модели САРМ – это оценка безрисковой ставки k_RF. В экономике нашей страны, как, впрочем, и других стран, на самом деле не существует активов, совершенно свободных от риска. Ценные бумаги ГКО в значительной степени свободны от риска неплатежа, но облигации ГКО подвержены, например, риску процентных ставок, а краткосрочные казначейские векселя – риску ставки реинвестирования.

Если на практике невозможно найти действительно свободную от риска ставку, какую ставку тогда нужно использовать с применением модели САРМ? Исследование показало, что примерно две трети фирм ориентируются на ставку долгосрочных облигаций ГКО.

Можно согласиться с этим выбором по следующим причинам.

1. Обыкновенные акции – это долгосрочные ценные бумаги, и хотя отдельный акционер может и не предполагать их длительного владения, большинство владельцев акций все – таки осуществляет долгосрочные инвестиции. Следовательно, разумно предположить, что «безрисковая составляющая» доходности акций определяется теми же долгосрочными инфляционными ожиданиями, что отражаются в доходности долгосрочных казначейских облигаций, а не векселей Казначейства.

2. Ставки доходности краткосрочных векселей, как показывает анализ, более неустойчивы, чем доходности казначейских облигаций, и, как отмечается большинством экспертов, более волатильны, чем стоимость капитала к_s большинства компаний.

3. Теоретически модель САРМ может использоваться для измерения доходности активов за определенный период. Когда она используется для оценки стоимости капитала для финансирования инвестиционных проектов, теоретически верным периодом анализа является срок жизни проекта. Поскольку многие проекты на практике являются долгосрочными, период расчета доходности по модели САРМ также должен быть долгосрочным.

4. Следовательно, ставка по долгосрочным казначейским облигациям – это наиболее логичный выбор для оценки безрисковой ставки, если нас интересует стоимость собственного капитала фирмы как составляющая ее средневзвешенной стоимости капитала.

Оценка премии за рыночный риск. Премия за рыночный риск RP_M – это ожидаемая разница между рыночной доходностью и безрисковой ставкой: k_M - k_RF. Ее можно оценить на основании: 1) исторических данных или 2) перспективных оценок.

Логика использования исторических оценокбазируется на предположении о том, что будущая ситуация в экономике будет незначительно отличаться от прошлой. Если эта гипотеза справедлива, то среднее арифметическое годовых значений доходности будет относительно верным приближением премии за риск на ближайшие годы. В свою очередь, оценку, основанную на среднем геометрическом, можно считать лучшей оценкой на более длительный период, скажем на период в двадцать лет. Однако весьма спорно, чтобы будущее было похожим на прошлое. Кроме того, выбор периода анализа может оказать большое влияние на результаты расчета премии за риск. Иногда расчеты премии за некоторые периоды в прошлом могут привести к отрицательным оценкам премии за риск, что противоречит как теории, так и здравому смыслу и является не более чем следствием случайных колебаний рыночных цен акций и облигаций.

При использовании перспективных оценок премии за риск наиболее общим подходом является применение модели дисконтирования денежных потоков (DCF) для оценки ожидаемой рыночной доходности 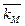. Если предположить, что ожидания инвесторов рациональны и требуемая ими доходность к_М = 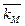, то зная 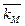, мы сможем оценить рыночную премию за риск RP_M= к_М - 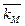и затем использовать эту оценку для расчета стоимости обыкновенного капитала отдельной компании. Еще раз отметим, что данная процедура использует тот факт, что если рынок находится в состоянии равновесия, то ожидаемая доходность рынка 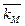будет в точности равняться также и требуемой инвесторами доходности рынка к_М:

=

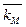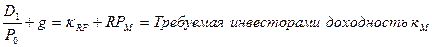
Поскольку величину дивидендов D₁ для рынка в целом (состояние рынка оценивается по индексам), можно предсказать с большой точностью и текущее значение индекса Р₀ также известно, главная трудность для аналитика на этом этапе – оценить g, среднегодовой темп прироста дивидендов в будущем. Здесь уже не обойтись без обращения к историческим оценкам роста или экспертным суждениям.

Оценка бета – коэффициентов.Оценка бета – коэффициентов является очень сложной и трудоемкой задачей, при решении которой применяются методы математического и регрессионного анализа. Однако отметим, что даже самые лучшие эконометрические оценки бета – коэффициентов для отдельной компании является не вполне точными, поскольку любой прогноз всегда носит приблизительный характер. Следовательно, менеджерам и финансовым аналитикам необходимо научиться мириться с некоторой неопределенностью результатов прогнозирования риска и стоимости собственного капитала их компаний.

Демонстрация применения модели САРМ. Чтобы продемонстрировать, как применяется подход, основанный на модели САРМ, на примере компании «А», предположим, что мы выяснили, что k_RF = 8%, RP_M = 6%, b_А=1,1, что указывает на то, что акции компании «А» чуть более рискованны, чем рынок в целом. Используя эти данные, получаем, что стоимость обыкновенного собственного капитала компании «А» равна 14,6%:

к_S = 8+6*1,1=14,6%.

Необходимо заметить, что, хотя и кажется, что подход САРМ позволяет получить удовлетворенную оценку к_S, его применение все – таки сопряжено с рядом трудностей. Во-первых, если портфели акционеров фирмы не являются достаточно хорошо диверсифицированными, они могут заботиться и о включении в доходность своих акций и компенсации автономного риска компании помимо рыночного риска. В этом случае действительную премию за риск нельзя будет измерить с помощью бета – коэффициента акций компании, а применение модели САРМ приведет к занижению оценки к_S. Более того, даже если метод САРМ и можно считать применимым в принципе, оценки по этому методу могут оказаться смещенными относительно верного значения стоимости капитала. Причина этого кроется в том, что: 1) как уже отмечалось, бывает сложно оценить ожидаемый инвесторами на будущие периоды бета – коэффициент компании; 2) нелегко спрогнозировать премию за рыночный риск.