Методы экстраполяции
Экстраполяция представляет метод прогнозирования, заключающийся в изучении сложившихся в прошлом и настоящем устойчивых тенденций развития процессов и явлений и переносе их на будущее. Метод экстраполяции применим, если используются следующие допущения: а) период времени, для которого построена функция, должен быть достаточным для выявлении тенденции развития; б) анализируемый процесс является устойчиво динамическим и обладает инерционностью, т.е. для значительных изменений характеристик процесса требуется время; в) не ожидается сильных внешних воздействий на изучаемый процесс, которые могут серьезно повлиять на тенденцию развития. Прогнозирование с помощью метода экстраполяции – один из простейших методов статистического прогнозирования. Его использование оправдано при недостаточном знании о природе изучаемого явления или отсутствии данных, необходимых для применения более совершенных методов прогнозирования.
Различают а) простую экстраполяцию, которая предполагает, что все действовавшие в прошлом и настоящем тенденции сохранятся в полном объеме, так как все действовавшие факторы останутся неизменными; б) прогнозную экстраполяцию, которая базируется на предположении об изменении факторов, определяющих динамику изучаемого процесса или явления.
Основу экстраполяции составляет изучение динамических рядов, представляющих собой упорядоченные во времени наборы измерений тех или иных показателей исследуемого объекта. В основе динамического анализа лежит понятие траектории, которая описывает состояние изучаемого процесса как функцию от времени: Q = Q(t), t 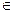 [0,T], [0,T] – отрезок времени.
[0,T], [0,T] – отрезок времени.
При этом время может учитываться как по интервалам, так и непрерывно. В первом случае функция называется динамическим рядом.
Использование экстраполяции имеет в своей основе предположение о том, что рассматриваемый процесс представляет собой сочетание двух составляющих: регулярной составляющей (Хt) и случайной переменной ( 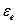 ). Временной ряд может условно представлен в виде: Yt = Xt +
). Временной ряд может условно представлен в виде: Yt = Xt + 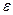 t.
t.
Регулярная составляющая называется трендом, тенденцией и характеризует существующую динамику развития процесса в целом. Случайная составляющая отражает случайные колебания (шумы процесса).
Показателями развития процесса являются абсолютный прирост, темп роста, темп прироста. Показатели изменения динамического ряда могут вычисляться на постоянной и переменой базе. Для обобщающей оценки скорости и интенсивности изменения динамического ряда используются различные средние характеристики, среди которых являются средний темп роста и средний темп прироста. Средний темп роста рассчитывают как среднее геометрическое и как среднее параболическое. Среднее геометрическое рассчитывается из последовательных цепных темпов роста:  ; среднее параболическое ориентировано на сумму динамического ряда и определяется из уравнения:
; среднее параболическое ориентировано на сумму динамического ряда и определяется из уравнения:
Задача ППЭ состоит в определении вида экстраполирующих функций Хt и 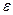 t на основе исходных эмпирических данных и параметров выбранной функции.
t на основе исходных эмпирических данных и параметров выбранной функции.
Методика построения трендовых моделей представляет сочетание качественного экономического анализа и формальных математико-статистических методов и включает несколько этапов: 1) Выбор класса функции тренда. Существует более 40 временных функций, отличающихся своими свойствами. Надо выбрать ту, которая отражает главные особенности динамики исследуемого показателя, прежде всего тип развития. Можно выделить 4 типа экономического роста: постоянный, увеличивающийся, уменьшающийся и рост с качественными изменениями характеристик на протяжении рассматриваемого периода. 2) Оценка параметров функции. Он проводится методами регрессионного анализа. 3) Расчет значений формальных критериев аппроксимации. Для характеристики близости тренда к аппроксимируемому динамическому ряду применяют несколько формальных критериев: сумма квадратов отклонений значений тренда от фактических значений, значение коэффициента детерминации и т.д. 4) Анализ остаточной компоненты динамического ряда. 5) Выбор функции тренда. Результатом предшествующих этапов является построение нескольких функций тренда для одного показателя. Выбор лучшей осуществляется путем сопоставления значений, возможностей экономической интерпретации и использования в прогнозировании.
МЕТОД ЛИНЕЙНОЙ экстраполяции. Сущность метода заключается в том, что прогнозные величины определяются на основе среднего прироста (снижения) исследуемого показателя за определенный период времени.
Пример. Предположим, у нас имеются данные об объеме ВНП страны за ряд лет:
Таблица - Объем ВНП страны
| Год | Объем ВНП | Прирост ВНП |
| 16,0 | - | |
| 21,8 | 5,8 | |
| 27,0 | 5,2 | |
| 32,0 | 5,0 | |
| 36,8 | 4,8 |
Рассчитаем средний темп прироста за четыре года: (5,8 + 5,2 + 5,0 + 4,8)/4 = 5,2
Определив средний темп прироста, рассчитаем прогнозное значение ВНП страны на 2000 год: Y2000 = Y1999 + 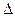 Y = 36,8 + 5,2 = 42,0
Y = 36,8 + 5,2 = 42,0
В тех случаях, когда показатели базисного и конечного прогнозного периода известны и следует определить годовые промежуточные показатели, используют метод линейной интерполяции, рассчитывая средний прирост за данный период времени:
Пример: Y2000= 205, Y2005 = 240. 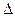 Y = (240 - 205)/5 = 7.
Y = (240 - 205)/5 = 7.
Y2002 = Y2000 + 2* 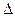 Y = 205 + 2*7 = 219.
Y = 205 + 2*7 = 219.
МЕТОД ПРОСТОЙ СРЕДНЕЙ. Применяется в тех случаях, когда в уравнении линейной зависимости Y = a + bx, коэффициент b = 0. При таком условии график будет представлен прямой параллельной горизонтальной оси графика, а прогноз будет состоять в расчете простой средней из всех имеющихся данных: Y =  Y/N.
Y/N.
Расчеты простой средней часто связывают с сезонными колебаниями, происходящими внутри общего тренда.
Пример. Имеются данные об объеме ВНП за ряд лет по кварталам:
| Год | 1 квартал | 2 квартал | 3 квартал | В целом за год | |
| Итого | |||||
| Средний объем | 294,5 |
Рассчитываем квартальный индекс: 1 квартал = 272:294,5 = 0,92; 2 квартал = 404:294,5 = 1,37;
3 квартал = 300:294,5 = 1,02; 4 квартал = 203:294,5 = 0,69.
Для того, чтобы составить прогноз объема ВНП по кварталам на 2000 год, надо прогнозное значение ВНП за данный год разделить на 4(количество кварталов) и умножить на соответствующий квартальный индекс. Предположим, что в 2000 году ВНП будет равен 1450. Тогда в 1 квартале будет произведено: (1450:4)*0,92= 333,5; 2 квартал = (1450:4)*1,37 = 496,625 и т.д.
МЕТОД наименьших квадратов. Позволяет подогнать функцию под некоторый набор численных значений и построить график функции по некоторой совокупности точек. Выбор этой функции считается наилучшим, если стандартное отклонение определяемое формулой:
E =  (dt – d’t)2
(dt – d’t)2 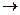 min оказывается сведено к минимальному значению.
min оказывается сведено к минимальному значению.
dt – фактические данные,
d`t – данные рассчитанной функции.
Как правило, используется линейная функция Y = a + bx.
Задача состоит в том, чтобы определить значения а и b, где
а – значение Y в базисном периоде,
b – угол наклона прямой.
Чтобы определить значения a и b используется система уравнений:
 Y = Na + b
Y = Na + b 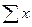
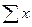 Y = a x + b x2 , где N - число периодов
Y = a x + b x2 , где N - число периодов
х – номер периода.
Пример. Имеются данные об объеме ВНП.
| Год | Y (ВНП) | x | x2 | xY | Y сглаженный |
| 108,4 | |||||
| 108,4 + 4,7 = 113,1 | |||||
| 108,4 + 2* 4,7 = 117,8 | |||||
| 108,4 + 3* 4,7 = 122,5 | |||||
| 108,4 + 4* 4,7 = 127,2 | |||||

|
Система уравнений выглядит следующим образом: 589 = 5а + 10b
1225 = 10ф + 30b.
Решая их, находим а = 108,4, b = 4,7.
Можно рассчитать ВНП 2000 года : Y2000 = Y1995 + 5b = 108,4 + 5*4,7 = 131,9.
В отдельных случаях лучшего соответствия теоретических данных эмпирическим можно достигнуть вычерчивая по точкам кривой сглаживания вида Y = abx, т.е. используя показательную функцию.
Если показательное уравнение логарифмировать, то значения коэффициентов а и можно определить методом наименьших квадратов:
 log Y = log a + x* log b.
log Y = log a + x* log b.
log a и log b находят, решая нормальные уравнения:  log Y = N log a +
log Y = N log a +  x log b.
x log b.
 x log Y =
x log Y =  x log a +
x log a +  x2 log b.
x2 log b.
Если определить х таким образом, что  x = 0, то
x = 0, то
log a =  log Y/ N, log b =
log Y/ N, log b =  x log Y/
x log Y/  x2.
x2.
МЕТОД СКОЛЬЗЯЩЕЙ СРЕДНЕЙ. При подготовке прогноза методом скользящей привязки число периодов, по которым производится суммирование фактических данных, несколько больше того числа, которое было установлено и которое желательно иметь для проведения необходимых расчетов. Необходимость выравнивания сезонных колебаний требует, чтобы суммарная продолжительность всех периодов была равна 1 году. Выравнивание сезонных колебаний происходит в силу того, что крайние значения тренда имеют тенденцию к взаимному погашению. Вовлечение в расчет скользящей средней большего числа временных периодов увеличивает эффект сглаживания и одновременно уменьшает чувствительность прогноза к данным последних периодов.
Движение скользящей средней во времени дает возможность учесть самую последнюю информацию и отказаться от использования более старых данных. Использование скользящей средней позволит подготовить качественный прогноз только тогда, когда данные будут относительно стабильны.
Индекс сезонных колебаний, вычисленный на основе скользящей средней, дает возможность улучшить качество прогноза. Индекс получают путем деления объема фактического производства в соответствующем периоде на величину центрированной скользящей средней за тот же период. Повысить надежность можно за счет усреднения значения нескольких индексов общих временных периодов.
Пример. Для разработки прогноза на 2000 год используем данные о квартальных объемах производства. Скользящие средние определяются исходя из разбивки года на кварталы. Можно рассчитать скользящую среднюю только за 2 квартал 1995 года путем деления суммы данных за четыре квартала данного года на 4: (190+370+300+220)/4= 270.
Для расчета следующей скользящей средней берут данные за 2-4 кварталы 1995 года и 1 квартал 1996 года. Аналогично поступают в дальнейшем.
Центрированная скользящая средняя находится только для третьего квартала путем деления суммы данных скользящей средней за 2 и 3 кварталы 1995 года: (270+292)/2 = 281.
Дальнейшие расчеты делаются аналогично, заменяя одно значение другим.
Индекс сезонных колебаний получают путем деления фактического объема производства на величину центрированной скользящей средней за тот же период. Для 3 квартала 1995 года: 300:281 = 1,07.
Таблица. Расчет значений скользящей средней и индексов сезонных колебаний
| Год | Квартал | Объем производства | Скользящая средняя | Центрированная скользящая средняя | Индекс сезонных колебаний |
| (190+370+300+220):4=270 | |||||
| (370+300+220+280):4=292 | (270+292):2 = 281 | 1.07 | |||
| (300+220+280+420):4=305 | (292+305):2= 298,5 | 0,74 | |||
| (220+280+420+310):4=307 | (305+307):2= 306 | 0,91 | |||
| (280+420+310+180):4=297 | (307+297):2= 302 | 1,39 | |||
| 1,04 | |||||
| 287,5 | 0,63 | ||||
| 276,5 | 0,98 | ||||
| 1,32 | |||||
| 1,00 | |||||
| 286,5 | 0,66 | ||||
| 301,5 | 1,00 | ||||
| 1,42 | |||||
| 307,5 | 0,94 | ||||
| 0,64 | |||||
| 1,01 | |||||
| 322,5 | 1,37 | ||||
На основе рассчитанных данных индекса сезонных колебаний заполняем таблицу 2 и делаем расчет скорректированного индекса.
Таблица 2 Расчет скорректированного индекса сезонных колебаний
| Год | 1 квартал | 2 квартал | 3 квартал | 4 квартал |
| 1.07 | 0,74 | |||
| 0,91 | 1,39 | 1,04 | 0,63 | |
| 0,98 | 1,32 | 1,00 | 0,66 | |
| 1,00 | 1,42 | 0,94 | 0,64 | |
| 1,01 | 1,37 | |||
| Итого | 3,90 | 5,50 | 4,05 | 2,67 |
| Средний индекс сезонных колебаний | 0.975 | 1,375 | 1,0125 | 0,6675 |
| Скорректированный индекс сезонных колебаний | 0,97 | 1,37 | 1,00 | 0,66 |
Средний индекс сезонных колебаний рассчитываем путем деления суммы индексов за данный квартал на количество данных: для 1 квартала: 3,90:4 = 0,975 и т.д.
Полученные средние индексы сезонных колебаний проверяют на точность расчета. Среднее значение всех квартальных индексов не должна превышать 1. В нашем случае:
(0.975 + 1,375 + 1,0125 + 0,6675): 4 = 1,0075
Так как индекс больше 1, его следует скорректировать, уменьшив на 0.0075.
Завершающая стадия – составление прогноза. Для этого берут центрированную скользящую среднюю за определенный период и умножают на скорректированный индекс сезонных колебаний. Для 2000 года мы должны взять центрированную скользящую среднюю за 1 квартал 1999 года (316) и умножить на скорректированный индекс сезонных колебаний за 1 квартал (0,97):
1 квартал 2000 года = 316*0,97 = 307.
И т.д.
ЭКСПОНЕНЦИАЛЬНОЕ СГЛАЖИВАНИЕ. При экспоненциальном сглаживании в равенство вводится постоянный коэффициент сглаживания 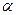 , придающий больший вес последним данным. Уравнение прогноза, учитывающее экспоненциальное сглаживание, записывается в виде:
, придающий больший вес последним данным. Уравнение прогноза, учитывающее экспоненциальное сглаживание, записывается в виде:
Fn = 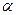 Yn-1 + (1 -
Yn-1 + (1 - 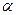 )Fn-1,
)Fn-1,
где Fn – прогноз предстоящего периода
Fn-1- прогноз на текущий год
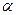 - коэффициент сглаживания
- коэффициент сглаживания
Yn-1- фактический объем прогнозируемого показателя в текущем году.
Коэффициент 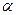 находится в интервале от 0 до 1.Чувствительность к происходящим изменениям повышается с увеличением коэффициента сглаживания и уменьшением числа рассматриваемых периодов (N). Связь между
находится в интервале от 0 до 1.Чувствительность к происходящим изменениям повышается с увеличением коэффициента сглаживания и уменьшением числа рассматриваемых периодов (N). Связь между 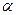 и N описывается отношением
и N описывается отношением 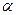 =
= 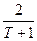 .
.
Поэтому, если нас не устраивает найденное количество периодов N, то мы легко можем найти значение 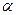 , которое нас устроит.
, которое нас устроит.
Дата добавления: 2017-08-01; просмотров: 14667;
