Применение экономико-математических методов в ППЭ

Идея оптимизации составляет одно из отличий подхода экономиста к анализу хозяйственной деятельности и решению экономических проблем. Программирование занимается решением задач по нахождению оптимальности. Поэтому оно хорошо подходит для анализа рационального поведения. В анализе оптимальности существует множество возможных величин, характеризующих результаты деятельности фирмы или экономики в целом. Программирование является исключительно математическим методом и не имеет никакого экономического содержания. Это означает, что результаты, полученные с помощью программирования, сами по себе ничего не говорят о деятельности хозяйствующих субъектов. Оно может только помочь оценить экономическую информацию, которую получили или готовы получить.

Преимущества программирования:

· Обеспечивает логически согласованную последовательность различных предпосылок;

· Позволяет использовать различные виды информации;

· Решает задачи большой размерности, учитывающие огромные объемы информации, различного типа ограничения и обеспечивающие реализацию многих альтернатив;

· Решает задачи с известной степенью точности;

· Могут систематически изучаться;

· Позволяют пояснить многие проблемы, связанные с разграничением задач и мерой ответственности между экспертами и политиками.

Использование экономико-математических методов предполагает формализованное описание экономического процесса и следующие этапы построениямодели:

1.формулируется предмет и цели исследования;

2.в экономической системе выделяются структурные или функциональные элементы, соответствующие данной цели, выявляются наиболее важные качественные характеристики этих элементов;

3.словесно, качественно описываются взаимосвязи между элементами модели;

4.вводятся символические обозначения для учитываемых характеристик экономического объекта и формализуются взаимосвязи между ними. Тем самым формулируется математическая модель;

5.проводятся расчеты математической модели и анализируются полученные решения.

Целевая функция описывает цель оптимизации и представляет собой зависимость показателей, по которым ведется оптимизация, от независимых переменных. Влияние каждой из переменных на величину целевой функции выражается коэффициентом – значением показателя, экстремум которого используется в качестве критерия оптимальности. Система ограничений отражает объективные экономические связи и зависимости в виде системы равенств и неравенств.

В экономико-математическом анализе используется широкий спектр математических методов. Наиболее простым является метод линейного программирования – направление математики, изучающее методы решения задач на экстремальные значения, которые характеризуются линейной зависимостью между переменными (неизвестными величинами) и линейным критерием. Необходимым условием постановки задачи является: 1) ограничение на ресурсы; 2) выбор количественно оцениваемого критерия оптимального плана.

Показатель, по которому оценивается мера эффективности плана, его оптимальность, называется критерием оптимальности. Критерий оптимальности должен удовлетворять следующим требованиям: 1) быть единственным, 2) количественно определяться, 3) находиться в линейной зависимости.

В общем виде задача линейного программирования выглядит следующим образом:

целевая функция: F(X) = c₁x₁+c₂x₂+ ….c_nx_n max;

условия ограничения в виде равенств или неравенств:

a₁₁x₁+a₁₂x₂+ … a_1nx_n= b₁

a₂₁x₂+a₂₂x₂+ … a_2nx_n= b₂

условие неотрицательности: х₁> 0, x₂>0 … x_n> 0.

Условие неотрицательности для экономического анализа имеет важное значение, так как свидетельствует о реальности протекаемого процесса.

В задачах линейного программирования исходные данные обычно определяются неточно. Поэтому важную роль играют методы стохастического линейного программирования, рассматривающего задачи, целевая функция и ограничения которых могут содержать случайные параметры.

НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ применяется в силу того, что в экономике существует большое количество нелинейных зависимостей. В этом случае целевая функция или условия ограничения становятся нелинейными относительно искомых переменных. Переменные входят в уравнения не в первой, а во второй или более высокой степени, перемножаются или делятся друг на друга. Данная форма программирования применяется в тех случаях, когда эффективность возрастает или убывает непропорционально изменению масштабов производства.

В общем виде задача нелинейного программирования может быть записана:

1) целевая функция F(X) =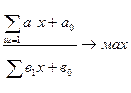

2) условия ограничения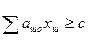

3) условие неотрицательности: х 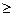0;

Могут быть различные комбинации целевой функции и условий ограничения с точки зрения сочетания линейности и нелинейности.

В числе методов нелинейного программирования можно выделить квадратичное и выпуклое программирование. Выпуклое программирование представляет собой совокупность специальных методов решения у которых выпуклы либо целевые функции, либо условия ограничения. Выпуклой считается область, если прямая, соединяющая две точки этой области, лежит полностью внутри данной области. Целью решения такой задачи является отыскание такого множества переменных, которое обеспечивает минимум выпуклой функции или максимум вогнутой. (Используется метод Лагранжа, матричные модели).

Квадратичное программирование – совокупность методов решения особого рода экстремальных задач, в которых условия ограничения линейны, а целевая функция является многочленом второй степени. Для решения такого типа задач могут применяться методы решения общей задачи выпуклого программирования.

ЦЕЛОЧИСЛЕННОЕ ПРОГРАММИРОВАНИЕ применяется в тех случаях, когда переменные принимают целочисленные значения (0,1,2 …). Простое округление результатов при расчетах может привести к значительным плановым ошибкам. Поэтому задачи целочисленного программирования требуют специальных методов решения. Различают задачи:

а) дискретного программирования. В этом случае вводится искусственная переменная R и условия задачи принимают вид:

целевая функция P = ax+by 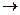max;

ограничения x 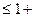R; y 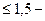R/2; R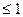

условия неотрицательности x 0; y 0; R 0.

Решение заключается в максимизации первоначальной целевой функции путем перебора переменных x, y, R, которые расположены в искусственно выпуклой области.

б) целочисленного программирования с булевыми переменными. Булевой переменной называют переменную, которая принимает значения 1 и 0. Использование таких переменных позволяет решать задачи о включении или не включении заданий в план.

Математическая модель имеет вид: целевая функция: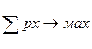

Условия ограничения: 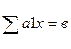х =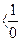

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ позволяет установить соотношение между экстремальными значениями целевой функции в задачах, характеризующихся различной продолжительностью процесса и различными начальными состояниями. При этом необходимо учитывать последствия найденного оптимального решения для последующих расчетов. Такой подход обуславливает выработку оптимальной стратегии. Процесс решения является многошаговым. Полученные на каждом этапе соотношения последовательно связаны между собой: полученные результаты вводятся в уравнения следующего шага. Т.о., при решении вариантных задач они разбиваются на отдельные этапы, каждый из которых решается самостоятельно. Тем самым сложная задача со многими переменными сводится к многим задачам с малым числом переменных. Это значительно сокращает объем вычислений и ускоряет процесс принятия управленческих решений.
Этим методом решаются задачи оптимизации с заданным критерием оптимальности, с определенными связями между переменными и целевой функцией, выраженными системой уравнений. При этом ограничения могут задаваться в виде равенств и неравенств. Динамическое программирование можно использовать как для решения задач, связанных с динамикой процесса или явления, так и для статических задач, связанных с распределением ресурсов.

К недостаткам следует отнести отсутствие единого универсального метода решения. Практически каждая задача, решаемая этим методом, характеризуется своими особенностями и трудностями и требует поиска наиболее приемлемой для ее решения методики. При поиске решения может оказаться, что процесс, рассматриваемый как многошаговый, имеет очень много состояний. В таком случае необходимо искать другие методы решения.

Динамическое программирование эффективно при определении оптимальной стратегии случайного (стохастического) процесса. Его протекание может быть различным в зависимости от случая, но вероятность каждого течения определена. Случайный процесс может быть непрерывным или дискретным. В рассматриваемом процессе независимой переменной является время, функция от независимой переменной – случайна. Случайный процесс характеризуется множеством значений его состояния. В зависимости от того, непрерывные или дискретные эти значения, случайный процесс будет непрерывным или дискретным.

При использовании динамического программирования необходимо:

· четко сформулировать задачу;

· сформировать целевую функцию и условия ограничения;

· подготовить исходную информацию по изучаемому процессу;

· определить альтернативные варианты развития процесса;

· выбрать оптимальный метод решения задачи;

· произвести расчеты;

· провести анализ и оценку полученных результатов.

Пример простейшей задачи динамического программирования : Планирование деятельности предприятия.

Целевая функция: (x₁, x₂ … x_n) = 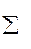(x_t-1, x_t)

Условия ограничения: x_t 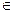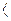d₁, d₂ … d_{k 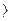;} t = 1,2 …n , где

(x_t-1, x_t) = 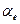(x_t-1, x_t) + 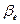(x_t-1, -r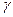_t) + (x_t), 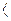d₁, d₂ … d_{k ;}

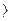t – время,

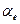(x_t-1, x_t) – затраты предприятия,

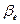(x_t-1, -r_t) – потери предприятия от отклонения выполнения плана,

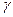(x_t) – текущие затраты,

d₁, d₂ … d_k - определенные по плану объемы производства продукции.

Экономические процессы характеризуются большими совокупностями однородных объектов. Поэтому нет необходимости изучать каждый элемент совокупности. Объектом исследования является определенная выборка. Полученные характеристики такой выборки могут использоваться для сравнительной оценки элементов различных совокупностей или их характеристик, установления связей между отдельными величинами и прогнозирования на этой основе развития системы в будущем. Это предполагает использование статистических методов в прогнозировании.

Математическая статистика включает корреляционный, регрессионный, дисперсионный, факторный анализ и т.д.

В экономике между различными явлениями могут быть две формы зависимости: функциональная и корреляционная. Функциональная – зависимость, которая точно проявляется в каждом отдельном случае и подчинена принципу строго определенного соответствия между количественными признаками. Корреляционная – зависимость между явлениями и показателями, которая проявляется только в среднем, в массе наблюдений.

Построение корреляционной модели предполагает постановку задачи, сбор статистических данных. Эти данные набираются на основе первичных документов и отчетных данных. Некоторые показатели могут быть получены только после предварительной обработки полученной информации. При сборе данных необходимо определить количество выборочных наблюдений - выборочную совокупность. Объем выборочных наблюдений осуществляется по формуле :

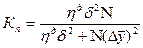
К_n - объем выборочных наблюдений;

N - величина генеральной совокупности;

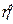- коэффициент доверия;

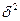- дисперсия значения признака в генеральной совокупности (показывает отклонение от средней величины);

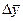- предельная ошибка случайной бесповоротной выборки (задается в зависимости от требований точности к получаемым результатам обработки).

После сбора данных осуществляется корреляционный анализ, состоящий из трех этапов: а) определяется форма связи исследуемых показателей (уравнение регрессии); б) проверяется теснота связи выбранных показателей, т.е. насколько полно выбраны факториальные признаки, как велико влияние неучтенных факторов; в) определяются численные значения постоянных коэффициентов уравнения.

Дисперсионный анализ – метод проверки гипотезы с помощью критериев, основанных на вычислении дисперсии. Наибольшее применение он находит для проверки связи между различными признаками.

Факторный анализ предполагает, что исследуемый процесс – многомерная случайная величина х = (х₁… х_n), подчиняющаяся нормальному распределению. В факторном анализе считается, что факторы, оказывающие влияние, надо определить; случайные величины независимы между собой. Наиболее перспективными направлениями факторного анализа является: сокращение числа экономических показателей, характеризующих какое-либо экономическое явление без существенной потери точности; получение обобщенных индексов; классификация экономических объектов, характеризующаяся набором независимых признаков; возможность построения и последующей статистической проверки гипотезы о сущности экономических явлений.

Цель факторного анализа – отыскание таких комбинаций х₁, …х_n, которые были бы как можно ближе к значению факторов f₁,…f_n. Обычно это двухстадийный процесс. Сначала оценивается факторная структура, т.е. необходимое число факторов для объяснения корреляции между переменными и нагрузки факторов на эти переменные. Затем – значения индивидуальных членов выборки для самих факторов. Важное место в содержательном факторном анализе занимает интерпретация факторов. Для оценки факторных нагрузок используют метод максимального правдоподобия, центроидный метод и т.д. При этом возможны различные предположения, например о некоррелированности факторов, о равенстве нулю какой-либо заранее выбранной факторной нагрузки и т.д.