Закономерности изменения технического состояния
1.4.1 Виды закономерностей
Для предупреждения отказов и неисправностей, а также для определения их источников, предъявления рекламационных претензий изготовителю или продавцу изделия мало констатировать сам факт возникновения отказа или неисправности. Необходимо знать причины, механизмы их возникновения и проявления, а также влияние различных отказов элементов на работоспособность автомобиля в целом, т.е. на способность выполнять транспортную работу. Иными словами, необходимо знать закономерности изменения технического состояния.
Процессы в природе и технике (в том числе и при технической эксплуатации) могут быть двух видов: процессы, характеризуемые функциональными зависимостями, и случайные (вероятностные, стохастические) процессы.
Для функциональных процессов характерна жесткая связь между функцией (зависимой переменной величиной) и аргументом (независимой переменной величиной), когда определенному значению аргумента (аргументов) соответствует определенное значение функции. Например, зависимость пройденного пути от скорости и времени движения.
Случайные процессы происходят под влиянием многих переменных факторов, значение которых часто неизвестно. Поэтому результаты вероятностного процесса могут принимать различные количественные значения (т.е. наблюдается рассеивание, или вариация) и называются случайными величинами (СВ).
Случайные процессы могут быть описаны пучком кривых Yi(t), характеризующих изменение технического состояния конкретных изделий 1, 2, 3,..., i,..., n (рисунок 1.7) от их наработки t. Иными словами, случайный процесс Y(t)может быть описан функцией, которая при каждом новом значении аргумента характеризуется набором нескольких случайных величин. Конкретные значения случайной функции при фиксированном значении аргумента t называются реализацией случайной величины.
При эксплуатации в основном приходится иметь дело со случайными процессами и величинами.
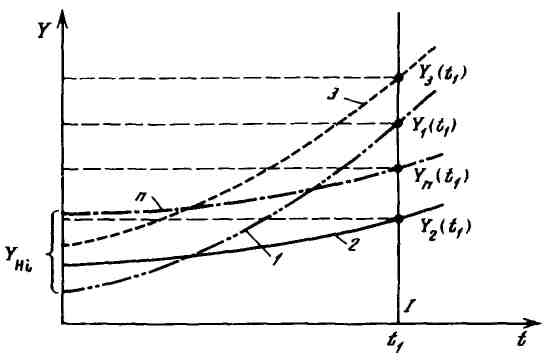
I — сечение случайного процесса, Y1—Yn — случайные величины – реализация случайного процесса Y(t) при t=t1.
Рисунок 1.7 – Схема формирования случайного процесса
1.4.2 Закономерности изменения технического состояния автомобиля по его наработке (закономерности ТЭА первого вида)
У значительной части узлов и деталей процесс изменения технического состояния в зависимости от времени или пробега автомобиля носит плавный, монотонный характер, приводящий к возникновению так называемых постепенных отказов. При этом характер зависимости может быть различным (рисунок 1.8). В случае постепенных отказов изменение параметра технического состояния конкретного изделия или среднего значения для группы изделий аналитически достаточно хорошо может быть описано двумя видами функций:
— целой рациональной функцией n-го порядка
| у=а0+а1l+а2l2+a3l3+...+апln; | (1.2) |
— степенной функцией
| y=a0+а1lb, | (1.3) |
где a0 — начальное значение параметра технического состояния;
l — наработка;
а1, а2,..., ап, b — коэффициенты, определяющие характер и степень зависимости у от l.
В практических вычислениях по формуле (1.2), как правило, достаточно использовать члены до третьего—четвертого порядков. Таким образом, зная функцию у=φ(l) и предельное Yпили предельно допустимое Yпд значение параметра технического состояния, можно аналитически определить из уравнения l=f(у)ресурс изделия или периодичность его обслуживания.
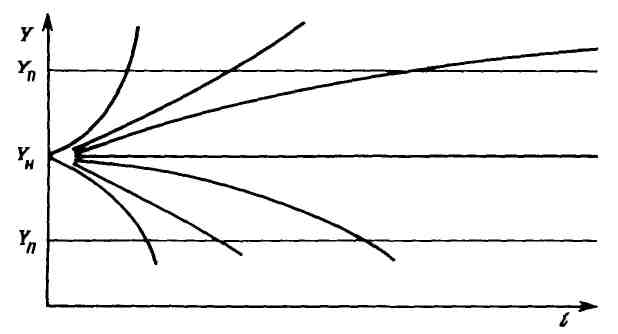
Yн, Yп — начальное и продельное значения параметра
Рисунок 1.8 – Возможные формы зависимости параметра технического
состояния Y от наработки l
Достаточно часто закономерности изменения параметров (например, зазора между накладками и тормозными барабанами, свободного хода педали сцепления и др.) описываются линейными уравнениями вида
| y=a0+а1l, | (1.4) |
где а1—интенсивность изменения параметра технического состояния, зависящая от конструкции и условий эксплуатации изделий.
Закономерности первого вида характеризуют тенденцию изменения параметров технического состояния (математическое ожидание случайного процесса), а также позволяют определить средние наработки до момента достижения предельного или заданного состояния.
1.4.3 Закономерности вариации случайных величин (закономерности ТЭА второго вида)
При работе группы автомобилей приходится иметь дело не с одной зависимостью Y(t), которая была бы пригодна для всей группы, а с индивидуальными зависимостями Yi(t), свойственными каждому i-му изделию (рисунок 1.9). Применительно к техническому состоянию однотипных изделий причинами вариации являются: даже незначительные изменения от изделия к изделию качества материалов, обработки деталей, сборки; текущие изменения условий эксплуатации (скорость, нагрузка, температура и т.д.); качество ТО и ремонта, вождения автомобилей и др. В результате при фиксации для группы изделий определенного параметра технического состояния, например Yп, каждое изделие будет иметь свою наработку до отказа (см. рисунок 1.9, а), т.е. будет наблюдаться вариация наработки. Возникает вопрос: какую периодичность ТО планировать для группы однотипных автомобилей?
Если все изделия обслуживать с единой периодичностью lто, то будет иметь место вариация фактического технического состояния (см. рисунок 1.9, б), которая скажется на продолжительности выполнения работ, количестве расходуемого материала и запасных частей.
В этом случае возникают вопросы: какую трудоемкость и стоимость операции планировать, какие потребуются производственные площади, технологическое оборудование, персонал?
При технической эксплуатации приходится сталкиваться и с другими СВ: расход топлива однотипными автомобилями даже на одинаковых маршрутах; расход запасных частей и материалов; число требований на ремонт в течение часа, смены работы поста ремонтной мастерской, станции ТО; число заездов на АЗС и др. Все это сказывается на нормировании и организации ТО и ремонта, определении необходимых для этого ресурсов.
Для решения этих задач необходимо уметь оценивать вариацию СВ.
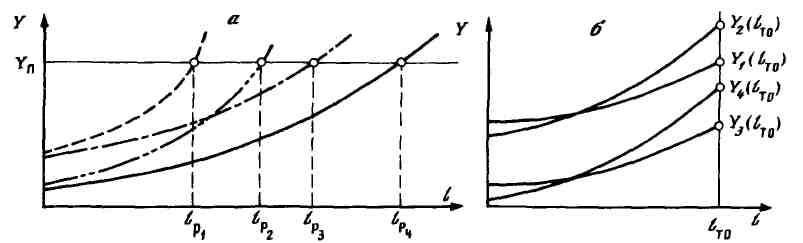
а — наработки (lр1 —lр4) при фиксации Yп; б — параметры технического состояния [Y1(lто)—Y4(lто)] при фиксации наработки l
Рисунок 1.9 – Вариации СВ
1.4.4 Оценки случайных величин
Рассмотрим простейшие методы оценки СВ. Исходные данные – результаты наблюдений за изделиями или отчетные данные, которые выявили индивидуальные реализации случайных величин (например, наработки на отказ, фактический расход топлива, материалов и т.д.).
1 Случайные величины (от 1 до n) располагают в порядке возрастания или убывания их абсолютных значений:
x1=xmin; x2; x3; x4;…;xi;…; xn-1; xn=xmax.
2 Точечные оценки CB:
— среднее значение СВ
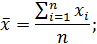
| (1.5) |
— размах СВ
| z=xmax-xmin; | (1.6) |
— среднеквадратическое отклонение, характеризующее вариацию,
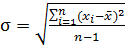 ; ;
| (1.7) |
— коэффициент вариации
| υ=σ/х. | (1.8) |
В ТЭА различают СВ
— с малой вариацией: υ≤0,1;
— со средней вариацией: 0,1≤υ≤0,33;
— с большой вариацией: υ>0,33.
Точечные оценки позволяют предварительно судить о качестве изделий и технологических процессов. Чем ниже средний ресурс и выше вариация (σ, υ, z), тем ниже качество конструкции и изготовления (или ремонта) изделия. Чем выше коэффициент вариации показателей технологических процессов ТЭА (трудоемкость, простои в ТО или ремонте, загрузка постов и исполнителей и др.), тем менее совершенны применяемые организация и технология ТО и ремонта.
3 Вероятностные оценки СВ. При вероятностных оценках рекомендуется размах СВ разбить на несколько (как правило, не менее 5—7 и не более 9—11) равных по длине Δx интервалов. Далее следует произвести группировку, т.е. определить число случайных величин, попавших в первый (n1), второй (n2) и остальные интервалы. Это число называется частотой. Разделив каждую частоту на общее число случайных величин (n1+n2+…+nn=n), определяют частость ω=ni/n. Частость является эмпирической (опытной) оценкой вероятности Р.
4 Обычно применяется следующая буквенная индексация рассмотренных событий и понятий:
— F (failure) — отказ, авария, повреждение, вероятность этих событий;
— R (reliability) — безотказность, надежность, прочность, вероятность этих событий;
— Р (probability) — вероятность.
Вероятность отказа может быть получена также последовательным суммированием интервальных вероятностей за наработку X, т.е.
| F(x)=p1+p2+…+pj, | (1.9) |
где j — номер интервала, соответствующий наработке X.
5 Следующей характеристикой случайной величины является плотность вероятности (например, вероятности отказа) f(x) — функция, характеризующая вероятность отказа за малую единицу времени при работе узла, агрегата, детали без замены. Если вероятность отказа за наработку F(x)=т(х)/п, то, дифференцируя ее при п=const, получим плотность вероятности отказа
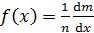 , ,
| (1.10) |
где dm/dx — элементарная «скорость», с которой в любой момент времени происходит приращение числа отказов при работе детали, агрегата без замены.
Так как f(x)=F'(x), то
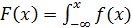 . .
| (1.11) |
Поэтому F(x)называют интегральной функцией распределения, а f(х) — дифференциальной функцией распределения. Так как
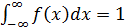 , a
, a 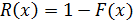 ,
,
то
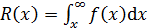 .
.
Имея значения F(x)или f(x), можно произвести оценку надежности и определить среднюю наработку до отказа
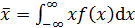 . .
| (1.12) |
6 При оценке качества изделий, нормировании ресурсов, в системе гарантийного обслуживания применяют гамма-процентный ресурс xγ.Это интегральное значение ресурса xγ, которое вырабатывает без отказа не менее γ процентов всех оцениваемых изделий, т.е.
R=P{xi>xγ}≥γ.
В ТЭА обычно принимаются γ=80, 85, 90 и 95 %. В рассматриваемом примере при γ=95 % xγ=7 тыс. км (таблица 1.4).
Риск отказа изделия F в данной ситуации, т.е. более раннее достижение изделиями гамма-процентного ресурса, составляет около 5 %.
Гамма-процентный ресурс используется при определении периодичности ТО по заданному уровню безотказности γ. Выражение lто=xγ означает, что обслуживание с периодичностью lто гарантирует вероятность безотказной работы R≥γ и отказа F≤(1-γ).
Если организаторы производства без технико-экономического анализа назначали периодичность, например, lто=10 тыс. км (см. таблицу 1.4), то примерно 18 изделий из 100 (n1=6 и n2=12, т(х)=18) откажут ранее назначенного ТО, т.е. вероятность отказа
F(x≤10)=P{xi<(X=10)}=m(x)/n=18/100=0,18.
Остальные 82 % изделий (19+25+20+13+5) имеют потенциальную наработку на отказ xi>10 тыс. км. Следовательно, ТО им будет произведено ранее, чем они могут отказать, и вероятность их безотказной работы
R(x>10)=P{xi<(X=10)}=[n-m(x)]/n=(100-18)/100=0,82.
Для первых отказов невосстанавливаемых изделий и взаимно дополняющих событий (отказ – работоспособное состояние) имеет место условие F(x)+R(x)=0,18+0,82=1, т.е., зная вероятность отказа, можно определить вероятность безотказной работы и наоборот.
7 Используя данные таблицы 1.4, можно также определить некоторые точечные оценки СВ.
Среднее значение СВ
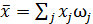 , ,
| (1.13) |
где j — номер интервала.
Для данных таблицы 1.4 имеем:
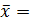 7 0,06+9 0,12+11 0,19+13 0,25+15 0,20+17 0,13+19 0,05=13,0 тыс. км.
7 0,06+9 0,12+11 0,19+13 0,25+15 0,20+17 0,13+19 0,05=13,0 тыс. км.
Таким образом, если бы периодичность ТО равнялась средней наработке на отказ, то более 60 % изделий в рассматриваемом примере отказали бы до обслуживания.
Среднеквадратическое отклонение
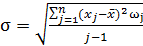 =1,26 тыс. км,
=1,26 тыс. км,
где j — число интервалов.
Коэффициент вариации
υ=σ/  =1,26/13≈0,1.
=1,26/13≈0,1.
8 Важным показателем надежности является интенсивность отказов λ(х) — условная плотность вероятности возникновения отказа невосстанавливаемого изделия, определяемая для данного момента времени при условии, что отказа до этого момента не было. Аналитически для получения λ(х)необходимо элементарную вероятность dm/dx отнести к числу элементов, не отказавших к моменту х, т.е.
λ(x)=dm/dx:[n-m(x)].
Так как вероятность безотказной работы
R(x)=[n-m(x)]/n,
то
λ(x)=dm/dx/[nR(x)].
Учитывая, что
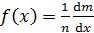 ,
,
получаем
λ(x)=f(x)/R(x).
Таким образом, интенсивность отказов равна плотности вероятности отказа, деленной на вероятность безотказной работы для данного момента времени или пробега.
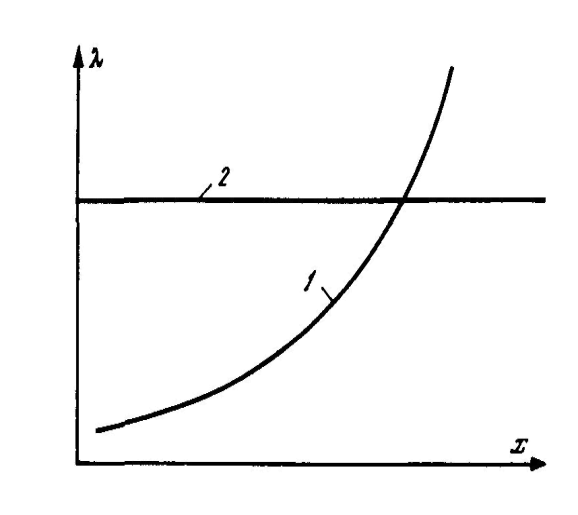
Рисунок 1.10 – Изменение интенсивности постепенных (1) и внезапных (2) отказов
Так как R(x)=1-т(х)/п, то после дифференцирования

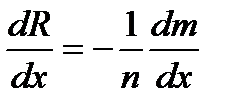 .
.
Так как
λ(x)=dm/dx/[nR(x)].
то можно записать:
λ(x)=-dR/dx/R(x),
откуда после интегрирования
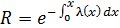
| (1.14) |
Это универсальная формула определения вероятности безотказной работы невосстанавливаемого элемента для любого закона распределения. Зная интенсивность отказов, можно для любого момента времени или пробега определить вероятность безотказной работы. Существуют внезапные и постепенные отказы (рисунок 1.10). Последние описывают работу так называемых стареющих элементов.
9 Наглядное представление о величине и вариации СВ дает их графическое изображение: гистограммы (1, рисунок 1.11) и полигоны (2, рисунок 1.11) распределения, а также интегральные функции распределения вероятностей отказа (3, рисунок 1.11) и безотказной работы (4, рисунок 1.11) и дифференциальные функции или законы распределения случайной величины (рисунок 1.12).
10 В ряде случаев законы распределения случайных величин могут быть описаны аналитически, как функции параметров этих законов. Такие аналитические зависимости имеются для нормального, экспоненциального и ряда других законов распределения СВ, описывающих процессы ТЭА.
Общий вид закона распределения:
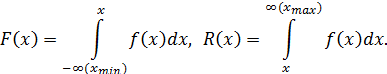
| (1.15) |
причем
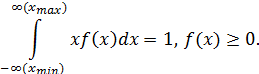
| (1.16) |
Для процессов технической эксплуатации и непрерывных СВ наиболее характерны следующие законы распределения.
Нормальный закон распределения (двухпараметрический: σ и x). Такой закон формируется, когда на исследуемый процесс и его результат влияет сравнительно большое число независимых (или слабозависимых) элементарных факторов (слагаемых), каждое из которых в отдельности оказывает лишь незначительное действие по сравнению с суммарным влиянием всех остальных.

| (1.17) |
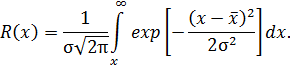
| (1.18) |
Экспоненциальный закон (однопараметрический – X). При экспоненциальном законе распределения вероятность безотказной работы не зависит от того, сколько проработало изделие с начала эксплуатации, а определяется конкретной продолжительностью рассматриваемого периода или пробега Δх, называемого временем выполнения задания. Таким образом, эта модель не учитывает постепенного изменения параметров технического состояния, например, в результате изнашивания, старения и других причин, а рассматривает так называемые нестареющие элементы и их отказы. Экспоненциальный закон используется чаще всего при описании внезапных отказов, продолжительности разнообразных ремонтных воздействий и в ряде других случаев:
| f(x)=λexp(-λx); | (1.19) |
| R(x)=exp(-λx). | (1.20) |
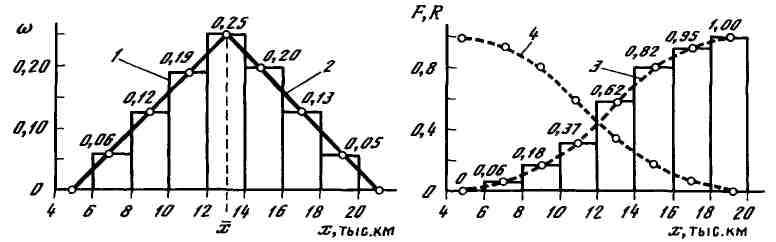
1 — гистограмма, 2 — полигон распределения, 3 — интегральная функция вероятности отказов и 4 — безотказной работы
Рисунок 1.11 – Графическое изображение случайной величины
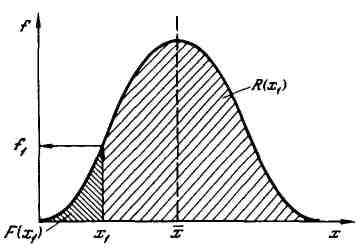
Рисунок 1.12 – Дифференциальная функция распределения – закон распределения СВ
Для этого закона λ=1/  ;
;  =σ; υ=1.
=σ; υ=1.
Закон распределения Вейбулла проявляется в модели так называемого слабого звена. Если система состоит из группы независимых элементов, отказ каждого из которых приводит к отказу всей системы, то в такой модели рассматривается распределение времени (или пробега) достижения предельного состояния системы как распределение соответствующих минимальных значений xi отдельных элементов:
xc=min(x1; x2;…; xn).
Функция распределения этой величины может быть выражена следующей зависимостью:
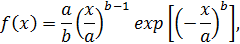
| (1.21) |
где a и b — параметры распределения.
Примером использования распределения Вейбулла является распределение ресурса подшипника качения. Этот ресурс ограничивается ресурсом одного из элементов (шарика, ролика, конкретного участка сепаратора и т.д.).
Значение аналитических зависимостей состоит в том, что если известен вид закона (на основе опыта, литературных источников, наблюдений) и его параметры, то можно расчетными методами, не проводя объемных наблюдений, воспроизвести (прогнозировать) ожидаемые вероятности отказов и других состояний изделий и процессов. Например, для нормального закона необходимо знать два параметра (  , σ), а для экспоненциального – один (
, σ), а для экспоненциального – один (  или λ), чтобы рассчитать вероятность отказов и безотказной работы (приложение Б).
или λ), чтобы рассчитать вероятность отказов и безотказной работы (приложение Б).
1.4.5 Примеры практического использования аналитических зависимостей
Если на основании имеющихся наблюдений или анализа механизма возникновения отказов можно предположить о реализации определенного теоретического закона распределения СВ, то соответствующие показатели можно рассчитать аналитически.
Так, для нормального закона при расчетах часто пользуются понятием нормированной функции Ф(z), для которой принимается новая случайная величина z=(х-  )/σ, так называемое нормированное отклонение. Тогда
)/σ, так называемое нормированное отклонение. Тогда
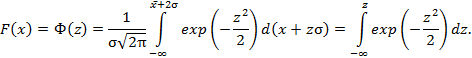
| (1.22) |
Для нормированной функции составлены таблицы, облегчающие расчеты (приложение Б).
Пример 1. Определить вероятность первой замены детали при наработке автомобиля с начала эксплуатации 70 тыс. км. Распределение наработки до первого отказа подчиняется нормальному закону с параметрами:  =95 тыс. км; σ=30 тыс. км.
=95 тыс. км; σ=30 тыс. км.
Используя понятие нормированной функции, определим нормированное отклонение
z=(x-  )/σ=(70-95)/30=-0,83.
)/σ=(70-95)/30=-0,83.
P(x)=Ф(z)=Ф(-0,83).
По приложению Б находим Ф(-0,83)≈0,20.
Таким образом, примерно 20 % автомобилей потребуют замены деталей при пробеге с начала эксплуатации до 70 тыс. км.
Вероятность отказа в интервале пробега x1-x2 определяется разностью P(x2)-P(x1)=Ф(z2)-Ф(z1).
Пример 2. Определить вероятность отказа той же детали в интервале пробега от x1=70 тыс. км до x2=125 тыс. км. Определяем: z1=-0,83; z2=(125-95)/30=1. По приложению 5 находим Ф(-0,83)=0,20; Ф(1)=0,84. Таким образом, вероятность отказа детали в интервале пробега 70—125 тыс. км составляет 0,64, т.е. у 64 % автомобилей в этом интервале пробега ожидается отказ детали и потребуется ее замена или ремонт.
Аналогичные таблицы имеются для экспоненциального и ряда других законов распределения.
Таким образом, умение оценивать случайные величины позволяет в реальной эксплуатации:
— во-первых, перейти от ожидания стихийного появления событий (отказы изделия, требования на услуги ТО и ремонт, заправку и др.) к инструментальному описанию и объективному предвидению их реализаций с определенной вероятностью, что позволяет подготовить и приспособить производство к эффективному освоению соответствующих требований;
— во-вторых, принять риск в качестве объективной реальности, свойственной любой деятельности, особенно эксплуатационной. Поэтому для успешной производственной деятельности важно стремиться не полностью исключить риск (что нереально для случайных процессов), а уметь его оценить и произвести выбор с учетом возможных отрицательных и положительных последствий.
Дата добавления: 2017-08-01; просмотров: 8030;
