Предметы (объекты), составляющие данное множество, называют его элементами.
Логика высказываний
Основные понятия
Истинностные значения «истина» и «ложь» будем обозначать прописными буквами И и Л соответственно.
Высказывание называется простым (элементарным), если оно рассматривается как некое неделимое целое. Сложным (составным) называется высказывание, составленное из простых с помощью логических связок (операций).
Основными логическими операциями над высказываниями являются: отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность, неравнозначность.
Отрицанием (инверсией) высказывания P называется высказывание, истинное тогда и только тогда, когда высказывание P ложно, и ложное в противном случае. Обозначения:  , ù P. Читается: «не P». Отрицание определяется таблицей истинности (табл. 4.1).
, ù P. Читается: «не P». Отрицание определяется таблицей истинности (табл. 4.1).
Конъюнкцией (операцией «И», логическим произведением) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания, и ложное во всех других случаях. Обозначения: P&Q, P×Q, PÙQ. Читается: «P и Q». Конъюнкция определяется таблицей истинности (табл. 4.2).
Дизъюнкцией (операцией «ИЛИ», логической суммой) двух высказываний P и Q называется высказывание, ложное тогда и только тогда, когда оба высказывания ложны, и истинное – во всех других случаях. Обозначения: PÚQ, P+Q. Читается: «P или Q» (понимается как неразделительное «или»). Дизъюнкция определяется таблицей истинности (табл. 4.3).
Импликацией (логическим следованием) двух высказываний P и Q называется высказывание, ложное тогда и только тогда, когда P истинно, а Q ложно, и истинное – во всех других случаях. Обозначения: P®Q, PÉQ. Читается: «если P, то Q», «P влечет Q»). Высказывание P называется посылкой импликации, а высказывание Q - заключением. Импликация определяется таблицей истинности (табл. 4.4).
Эквивалентностью (равнозначностью, эквиваленцией) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинностные значения P и Q совпадают, и ложное в противном случае. Обозначения: P«Q, P~Q, PºQ. Читается: «P эквивалентно Q», «P, если и только если Q», «P равнозначно Q». Эквивалентность определяется таблицей истинности (табл. 4.5).
Неравнозначностью (исключающим «ИЛИ», сложением по модулю 2) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинностные значения P и Q не совпадают, и ложное – в противном случае. Обозначения: PÅQ, PDQ. Читается: «P неравнозначно Q», «либо P, либо Q», «или P, или Q» (понимается – в разделительном смысле). Неравнозначность определяется таблицей истинности (табл. 4.6).
Буквы, обозначающие высказывания, логические связки и скобки, составляют алфавит языков логики высказываний: алгебры логики и исчисления высказываний.
Логической формулой называется выражение, составленное из обозначений высказываний, логических операций и скобок, и удовлетворяющее следующим условиям:
- любая переменная, обозначающая высказывание, - формула;
- если P и Q – формулы, то 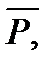 P&Q, PÚQ, P®Q, P«Q, PÅQ – формулы;
P&Q, PÚQ, P®Q, P«Q, PÅQ – формулы;
- других формул нет.
Пример 4.1. Представить логическими формулами следующие высказывания:
1. «Сегодня понедельник или вторник».
2. «Идет дождь или снег».
3. «Если идет дождь, то крыши мокрые. Дождя нет, а крыши мокрые».
4. «Что в лоб, что по лбу».
Решение.
1. Составное (сложное) высказывание «Сегодня понедельник или вторник» состоит из двух простых:
P – «Сегодня понедельник»; Q – «Сегодня вторник».
Высказывания P и Q соединены связкой «или» в разделительном смысле. Поэтому данное высказывание представимо логической формулой:PÅQ.
2. Составное высказывание «Идет дождь или снег» состоит из двух простых:
P – «Идет дождь»; Q – «Идет снег».
Высказывания P и Q соединены связкой «или» не в разделительном, а в обычном смысле. Таким образом, логическая формула имеет вид:P Ú Q.
3. Первое предложение «Если идет дождь, то крыши мокрые» включает два простых высказывания:
P – «Идет дождь»; Q – «Крыши мокрые».
Высказывания P и Q соединены связкой «если ¼ , то ¼»:P ® Q.
Второе предложение «Дождя нет, а крыши мокрые» также как и первое включает высказывания:
P – «Идет дождь»; Q – «Крыши мокрые».
Союз “а” имеет смысл связки «и», кроме того высказывание P используется с отрицанием, т.е. второе предложение представляется в виде:  & Q.
& Q.
Далее, объединяем оба предложения в одно высказывание связкой &:(P ® Q) &(  & Q).
& Q).
4. Составное высказывание «Что в лоб, что по лбу» состоит из двух простых:
P – «В лоб»; Q – «По лбу».
Высказывания P и Q соединены связкой «равнозначно»:P « Q.
Алгебра логики
Предикаты
Множества
Множество относится кпервоначальным понятиям науки, не определяемым через другие, более простые термины. Множество представляет собой определенную совокупность объектов, объединенных в единое целое в соответствии с некоторыми признаками и правилами.Множества обозначаются: A, B, C, X, Y, Z. Примеры множеств:
· множество всех атомов на Марсе;
· множество точек окружности;
· множество решений заданного уравнения;
· множество всех действительных чисел - R.
Г. Кантор (1845–1918 гг.) определял Множество как «многое, понимаемое как единое».
Наконец, определение Множества как «совокупности определенных различаемых объектов». Здесь для «объекта» важен просто сам факт принадлежностик Множеству – своеобразное характеристическое свойство.
Таким образом, в общем случае требуется задать характеристическое свойство, которым должны обладать все элементы множества. Способ задания «принадлежности», или попросту, путем перечисления годится, только для конечныхмножеств.
Множества обозначаются обычно большими латинскими буквами (необязательно), в их определении используется фигурные скобки ( {} ). Например, M = {a, b, c }.
Здесь определено 3-элементное множество путем простого перечисления элементов.
Еще пример, множество натуральных чисел: N= {1, 2, 3, …}.
Это бесконечное множество (о других его определениях еще придется говорить).
Предметы (объекты), составляющие данное множество, называют его элементами.
Кстати, порядокэлементов множества роли не играет: {1, 2, 4} = {2, 1, 4}.
Это – в отличие от набора (кортежа), где порядок важен и вместо фигурных скобок используются круглые: (1, 2, 4) ¹ (2, 1, 4).
Принадлежность элемента множеству символизируется знаком Î (похоже на греческую букву e): 4 Î М, 3 Ï М.
Считается, что повторяющихся элементов в множестве быть не должно (в отличие опять же от кортежа).
Множество может быть рекурсивно определяемым. При этом в правой части (после равенства) снова фигурирует имя множества. Например, N= {1, 2, 3, …} = {i : i = 1 или i = n +1, n Î N}.
Важнейшей характеристикой множества является его мощность (размер, норма, длина, кардинальное число). Это количество элементов множества. Например,
А = {1, 2, …, n} = {х : х Î N, 1 £ x £ n}, |А| = card (A) = n.
Кстати, | { {}, {} }| = |{Æ, Æ}| = 2.
Множество – конечное, если оно пустое или если его элементы могут быть пронумерованы 1, …, n, n Î N. В противном случае множество –бесконечное.
Над множествами можно выполнять любые арифметическиеоперации. Например,
А + В = { х : х = а + b, а Î А, b Î В}, т. е. речь идет о всевозможных суммах. И т. д.
Если каждый элемент множества А является вместе с тем и элементом множества В, то А называется подмножеством множества В:
А Í В - А содержится в В (или А включено в В) 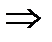 А подмножество В;
А подмножество В;
Если А Í В и А ¹ В, то А называется строгим (собственным) подмножеством множества В (обозначается А  В).
В).
Свойства подмножества: Æ Í А, А Í А, А Í Е.
Первое равенство, вообще-то, не следует из определения подмножества, которое приведено в начале раздела (дело в том, что ни одинэлемент не принадлежит Æ). В этом случае нужно расширитьпервоначальное определение или согласиться с условностьюэтого равенства (на «нет» и «суда нет»).
Множества А и В называются равными, если каждый элемент множества А является вместе с тем и элементом множества В, и каждый элемент В является элементом А:
А = В  А
А 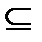 В и В
В и В 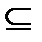 А.
А.
Множество Æ, не содержащее ни одного элемента, называется пустым множеством.Очевидно, что " А Æ Í А.
х Ï Æ при любом х, Æ = {}.
Пустое множество играет роль своеобразного нуля (0).
Например, ½Æ½ = 0, но ½íÆý½ = 1.
Непересекающиеся множества: А Ç В = Æ.
Пример: {1, 2} Ç {3, 4} = Æ.
Пример 1.1. Множество решений уравнения x2 + 1 = 0 во множестве R – пустое множество Æ.
Дата добавления: 2017-08-01; просмотров: 1892;
