Свойства операций над множествами

Пусть задано универсальное множество U. Тогда " A, B, C Ì U выполняются следующие свойства:

1. Идемпотентность: A È A = A, A Ç A = A.
2. Коммутативность:A È B = B È A, A Ç B = B Ç A.
3. Ассоциативность:A È (B È C) = (A È B) È C, A Ç (B Ç C) = (A Ç B) Ç C.
4. Дистрибутивность:A È (B Ç C) = (A È B) Ç (A È C), A Ç (B È C) = (A Ç B) È (A Ç C).
5. Поглощение:(A Ç B) È A = A, (A È B) Ç A = A.
6. Свойства нуля:A È Æ = A, A Ç Æ = Æ.
7. Свойства единицы:A È U = U, A Ç U = A.
8. Инволютивность:
9. Правила де Моргана:
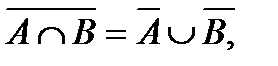
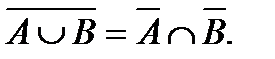
10. Свойства дополнения:
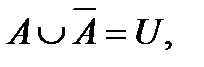
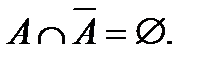
11. Выражение для разности:

Элементарные операции Ç и È взаимно дистрибутивны(распределительны). Например, Ç дистрибутивна относительно È: А Ç (В È С) = (А Ç В) È (А Ç С).

Вообще-то, надо бы еще одно равенство записать, где А распределяется справа от скобок. Но, в силу коммутативности Ç, это необязательно.

Итак, надо доказать L Í R и R Í L, где L, R – левая и правая части равенства:

L = А Ç (В È С), R = (А Ç В) È (В Ç С).

Доказательства подобного рода утверждений (равенств) можно проводить в трех формах:

- полностью словесная (где есть слова и словосочетания вида «если … то», «следует», …);

- символическая (сокращенно-условная);

- аналитическая (не всегда возможная).

Итак, используя вторую форму, получим:

х Î А Ç (В È С) Þ х Î А и х Î (В È С) Þ х Î А и (х Î В или х Î С) Þ

Þ (х Î А и х Î В) или (х Î А и х Î С) Þ

Þ (х Î А Ç В) или (х Î А Ç С) Þ х Î (А Ç В) È (А Ç С), т. е. L Í R («прямое» включение).

Обратное включение R Í L доказывается аналогично. Проще, однако, сделать двойные стрелки двунаправленными. Следует заметить, фактически свойство дистрибутивности «переведено» на уровень логических связок«и», «или» (они, как считается, взаимно дистрибутивны).

Вообще-то говоря, аргумент (причина) и следствие не всегда взаимно обратны, как здесь. Поэтому доказательство должно проводиться в обе стороны.

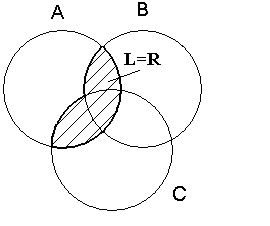Для иллюстрации могут использоваться диаграммы Венна (рис. 6). Но они не считаются достаточно доказательными.

Отчасти – в силу множественности их вариантов.

Рис. 6. Диаграмма Венна