Элементарные операции над множествами

Элементарных операций над множествами всего четыре:

пересечение, объединение, разность (дополнение), симметрическая разность.­­­­­

При этом первые три в большой степени аналогичны операциям (функциям) математической логики (алгебры логики) – конъюнкция (&), дизъюнкция (v), инверсия (ù ). Последняя четвертая операция является производной от первых трех.

Итак, пересечение множеств(рис. 1): А Ç В = {х : х Î А и х Î В}.

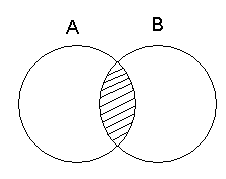Здесь символ «Ç» похож на русскую букву «П» («пересечение»), «и» – это логическая связка.

Рис. 1. Диаграмма Венна

Для пересечения множеств

Объединение множеств(рис. 2): А È В = {х : х Î А или х Î В}.

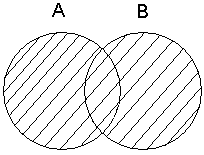«È» похоже на незавершенную русскую букву «О» («объединение»). ИЛИ здесь – не исключительное, т. е. это аналог «обычной» нестрогойдизъюнкции. Есть еще строгая дизъюнкция (ИЛИ-ИЛИ), в логике она обозначается « ».

Рис. 2. Объединение множеств

Утверждение: Для любых множеств А и В мощность объединения

çА Вç=çАç+çВç-çА Вç

Первые две операции фактически обладают теми же свойствами, что и операции &, v в алгебре логики.

Например, они коммутативны: А * В = В * А, и это, вообще-то, свойство логических связок «и», «или».

Они идемпотентны: А * А = А.

Свойство идемпотентности позволяет произвольно сжимать или расширять выражения, что весьма полезно в разного рода преобразованиях.

Кстати, {1, 2} Ç {2, 3} = {2},

{1, 2} È {2, 3} = {1, 2, 3},

но

{{1, 2}, {2, 3}} ¹ {1, 2 , 3}!

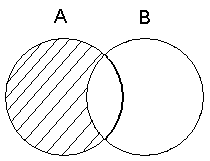
Разностьдвух множеств А \ В = {х : х Î А и х Ï В}. (рис. 3):

Рис. 3. Разность двух множеств

Заштрихованная область на рис. 3 соответствует дополнению В до А. Аналогично можно определить разность В \ А, или дополнение А до В (область В на рис. 3 без общей части).

Симметрическая разность (рис. 4): А D В = (А È В) \ (А Ç В).

Рис. 4. Симметрическая разность

Как видно, здесь реализуется исключительное ИЛИ (строгая дизъюнкция). В алгебре логике существует аналог: А Å В = (А v В) .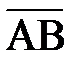

Действительно, (А v В) 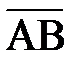= (А v В) (`А v `В ) = А`В v `АВ = А Å В.

Дополнение множества (до универсального): А¢ = Е \ А = {х : х Ï А}.

Множество и его дополнение однозначно определяются двумя равенствами (используются в доказательствах):

А Ç А¢ = Æ,

А È А¢ = Е.