На использование формул для перестановок и размещений

1.Сколько слов можно образовать из букв слова фрагмент, если слова должны состоять:

(а) из восьми букв, (б) из семи букв, (в) из трех букв?

Решение задачи:

В слове фрагмент 8 букв алфавита.

(а) Всевозможные перестановки 8 букв по восьми местам: А 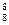= =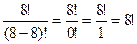P₈.

(б) Размещения 8 букв по 7 местам: А .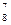

(в) Размещения 8 букв по 3 местам: А .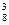

Ответ: P₈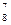, А , А .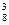

2.Сколькими способами можно расставить на полке 7 книг, если (а) две определенные книги должны всегда стоять рядом, (б) эти две книги не должны стоять рядом?

Решение задачи:

(а) Книги, которые должны стоять рядом, считаем за одну книгу. Тогда нужно расставить 6 книг по шести местам. Применяя формулу перестановок, получаем: P₆ = 6!. Мы учли перестановки шести книг, не учитывая порядок внутри тех книг, которые мы посчитали за одну. А так как две книги по двум местам можно разместить только двумя способами (P₂), то получаем окончательно следующее произведение: P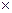₂ P₆ =2 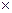6! = 1440.

(б) Способов переставить 7 книг существует P₇= 7!. Из них ‑ 2 6! способов поставить определенные книги вместе. Следовательно, способов поставить книги так, чтобы 2 заданные книги не стояли вместе существует: 7! ‑ 2 6!.

Ответ: 1440; . 7! ‑ 2 6!