Размещения (упорядоченные выборки).

Элементы комбинаторики

Принцип умножения

Пусть необходимо выполнить одно за другим одновременно r действий. Если первое действие можно вы­полнить n₁ способами, после чего второе - n₂ способами и т.д. до r - того действия, которое можно выполнить n_r спосо­бами, то все r действий вместе можно выполнить n₁, n₂…n_r способами.

Пример: Сколько существует двузначных чисел?

Способ 1: (принцип умножения)

Выбирается две цифры, поэтому r= 2. Первая цифра может быть любой, кроме 0. Потому n₁= 9. Вторая цифра может быть любой, т.е. n₂=10. итак двузначных чисел: n₁n₂=9 ^. 10=90.

Способ 2. (перо6ора)

10 20 30 ………..90

11 21 31 …………91 прямоугольная таблица 10 ^. 9=90

12 22 32 …………92

………………………….

19 29 39 ………...99

Пример: Бросают три игральные кости и наблюдают за числом очков, появившихся на каждой кости. Сколько различных исходов опы­та возможно?

Решение: Бросают три игральные кости, поэтому по принципу умножения r= 3, На выпавшей грани "первой" игральной кости может появить­ся одно очко, два очка, ... шесть очков. Поэтому n₁= 6. Анало­гично n₂= 6, n₃= 6. Итак, число всех исходов опыта n₁n₂n₃= 6 ^.6 ^.6=216.

Пример: Сколько существует нечетных трехзначных чисел?

Решение: По принципу умножения r = 3 ; n₁ = 9, т.к. первая цифра может быть любой, кроме 0; n₂ = 10, т. к. вторая цифра может быть любой ; n₃ = 5, т.к. третья цифра должна быть нечетной. Итак, всех возмож­ностей

n₁n₂n₃ =9 ^. 10 ^. 5=450.

Замечания к принципу умножения. Если на выполнение какого-ли­бо из r действий наложено ограничение, то подсчет удобнее начи­нать с выполнения именно этого действия.

Пример: В машине 7 мест, одно место водителя. Сколькими спо­собами могут сесть в машину 7 человек, если место водителя могут занять только трое из них?

Решение: По принципу умножения r = 7. Начнем с места водителя n₁ = 3, следующее место может занять любой из 6 оставшихся человек, т.е. n₂ = 6, следующее место может занять любой из 5 оставшихся человек и т.д. Поэтому n₃ = 5, n₄ = 4, n₅ = 3, n₆= 2, n₇ = 1.

Итак, всех возможностей: n₁ ∙n₂ ∙n₃∙ n₄∙ n₅∙n₆∙n₇ =3∙6∙5∙4∙3∙2∙1 = 2160.

Размещения (упорядоченные выборки).

Пусть А – множество, состоящее из элементов а₁, а₂,…, а_n.

Определение: Упорядоченные наборы, состоящие из r элементов множество А, будем называть размещениями из n элементов множества А по r элементов.

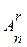– число размещений из n элементов по r элементов(r £n). Вычислим 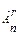по принципу умножения:

n₁₌ n,

n_{2 =}n-1, 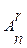₌ n(n-1)(n-2)….(n-r+1).

n_{3 =} n-2,

…………

n_r= n-(r-1) = n-r+1.

Здесь n, n-1, n-2,…,n-r+1 есть число возможностей для выбора первого, второго, третьего,… r – того элементов.

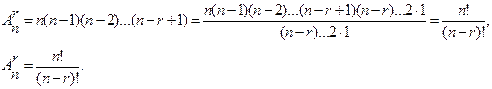
Перестановки

Определение: Размещения из n элементов по n элементов называются перестановки из n элементов.

P_n – число перестановок из n элементов.

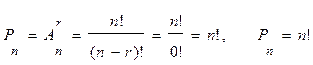
Пример: Сколькими способами могут 4 человека разместиться в 4-х местном купе железнодорожного вагона?

Решение: А = {1, 2, 3, 4} (4 места в купе вагона);

P₄ = 4! = 1∙2∙3∙4 = 24.