Сочетания (неупорядоченные выборки)

А = {а₁, а₂, а₃, …а_n}

Определение: Неупорядоченные наборы, состоящие из r элементов множества А, называются сочетаниями из n элементов по r элементов. (r 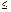n).

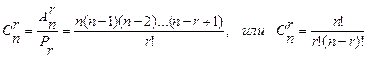
Пример: Студенту необходимо сдать 4 экзамена за 10 дней. Сколькими способами можно составить ему расписание, если в один день нельзя сдать более одного экзамена?

Решение: А = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} (10 дней). Поскольку в расписании учитывается порядок экзаменов, то мы имеем дело с упорядоченными выборками, т.е. с размещениями.

Пример: Подрядчику нужны 4 плотника, к нему с предложениями своих услуг обратилось 10 человек. Сколькими способами можно набрать рабочую силу?

А = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} (плотники).

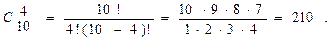
Пример. В розыгрыше первенства по футболу участвуют 10 команд. Известно, что те, кто займет первые 3 места, получают золотую, серебряную и бронзовую медали, а последние двое выбывают. Сколько различных результатов первенства может быть?

Решение: Нужно выполнить одно за другими два действия:

I. Из десяти команд выбрать три на три первых места.

II. После выполнения первого действия из оставшихся семи команд выбрать две на два последних места.

Итак, по принципу умножения r = 2 ;

n₁= 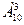=10ž9ž8=720; n₂= 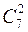= =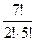21.

Различных результатов первенства может быть:

n₁n₂= 720 ^. 21=15120.

Варианты заданий

Решить комбинаторные уравнения

1.

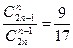
2.

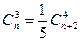
3.

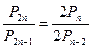
4.

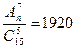
5.

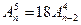
6.

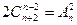
Самостоятельная работа №2 Расчет количества выборок заданного типа в заданных условиях