Методы оценки доходности финансовых активов

Чтобы определить распределение вероятностей случайной величины r, необходимо знать, какие фактические значения r_i принимает данная величина и какова вероятность Р_i каждого подобного результата. При этом инвестора интересует доходность инвестиций в конце инвестиционного, холдингового периода, то есть будущие значения r_i, которые в начальный момент инвестирования неизвестны. Значит, инвестор должен оперировать ожидаемым, будущим распределением случайной величины r.

Существует два подхода к построению распределения вероятностей – субъективный и объективный, или исторический. При использовании субъективного подхода инвестор должен определить возможные сценарии развития экономической ситуации в течение холдингового периода, оценить вероятность каждого результата и ожидаемую при этом доходность ценной бумаги.

Субъективный подход имеет важное преимущество, поскольку позволяет оценивать сразубудущее значение доходности. Однако он не находит широкого применения, поскольку для обычного инвестора очень трудно сделать оценку вероятностей экономических сценариев и ожидаемую при этом доходность.

Чаще используетсяобъективный, илиисторический подход. В его основе лежит предложение о том, что распределение вероятностей будущих (ожидаемых) величин практически совпадает с распределением вероятностей уже наблюдавшихся фактических, исторических величин. Значит, чтобы получить представление о распределении случайной величины r в будущем достаточно построить распределение этих величин за какой-то промежуток времени в прошлом [13, 25].

Как показывают исследования западных экономистов, для рынка акций наиболее приемлемым является промежуток 7-10 шагов расчета. В отличие от субъективного подхода, который предполагает разную вероятность различных значений доходности, при объективном подходе каждый результат имеет одинаковую вероятность, поскольку при N наблюдениях случайной величины вероятность конкретного результата составляет величину 1/N. Например, если исследуется доходность акции за предшествующие 10 лет, то вероятность каждой годовой доходности r_i составляет 1/10.

Наиболее часто в теории инвестиционного портфеля используется среднее арифметическое значение доходности отдельной ценной бумаги. Напомним, что если r_t (t = 1,2,…,N) представляют собой значения доходности в конце t-го периода, а P_t – вероятности данных значений доходности, то

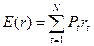, (21)

где E(r) – среднее арифметическое значение доходности; N – количество лет, в течение которых велись наблюдения.

В случае объективного подхода P_t=1/N, поэтому формула примет вид

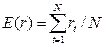. (22)

Наиболее часто риск ценной бумаги измеряют с помощью дисперсии σ² и стандартного отклоненияσ:

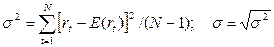. (23)

Под ожидаемой доходностью портфеля понимается средневзвешенное значение ожидаемых значений доходности ценных бумаг, входящих в портфель. При этом «вес» каждой ценной бумаги определяется относительным количеством денег, направленных инвестором на покупку этой ценной бумаги. Ожидаемая доходность инвестиционного портфеля равна [40]

, (24)

где E(r_p) – ожидаемая доходность портфеля; W_i – доля в общих инвестиционных расходах, идущая на приобретение i-й ценной бумаги («вес» i-й ценной бумаги в портфеле); E(r_i) – ожидаемая доходность i-й ценной бумаги; n – число ценных бумаг в портфеле.

Измерение риска портфеля. При определении риска портфеля следует учитывать, что дисперсию портфеля нельзянайти как средневзвешенную величин дисперсий входящих в портфель ценных бумаг. Это объясняется тем, что дисперсия портфеля зависит не только от дисперсий входящих в портфель ценных бумаг, но также и от взаимосвязи доходностей ценных бумаг портфеля друг с другом. Риск портфеля объясняется не только индивидуальным риском каждой отдельно взятой ценной бумаги портфеля, но и тем, что существует риск воздействия изменений наблюдаемых ежегодных величин доходности одной акции на изменения доходности других акций, включаемых в инвестиционный портфель.

Меру взаимозависимости двух случайных величин измеряют с помощью ковариации и коэффициента корреляции.Положительная ковариация означает, что в движении доходности двух ценных бумаг имеется тенденция изменяться в одних и тех же направлениях: если доходность одной акции возрастает (уменьшается), то и доходность другой акции также возрастет (уменьшится). Если же просматривается обратная тенденция, то есть увеличению (уменьшению) доходности акций одной компании соответствует снижение (увеличение) доходности акций другой компании, то считается, что между доходностями акций этих двух компаний существует отрицательная ковариация.

Когда рассматриваются величины доходности ценных бумаг за прошедшие периоды, то ковариация подсчитывается по формуле [14]

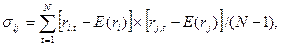(25)

где σ_i,j – ковариация между величинами доходности ценной бумаги i и ценной бумаги j; r_i,t и r _j,t – доходность ценных бумаг i и j в момент времени t; E(r_i),E(r_j) – ожидаемая (средняя арифметическая) доходность ценных бумаг i и j; N – общее количество лет наблюдения.

При определении степени взаимосвязи двух случайных величин используют относительнуювеличину – коэффициент корреляции ρ_ij:

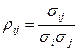. (26)

Коэффициент корреляции между доходностью ценных бумаг i и j равен отношению ковариации доходности этих ценных бумаг к произведению их стандартных отклонений [14].

Значения ρ_ij изменяются в пределах: - 1 ≤ ρ_ij ≤ +1 и не зависят от способов подсчета величин σ_ij и σ_i, σ_j. Это позволяет более точно оценивать степень взаимосвязи доходности двух ценных бумаг: если ρ_ij > 0, то доходность ценных бумаг i и j имеет тенденцию изменяться в одних и тех же направлениях, то есть, когда доходность i-ой ценной бумаги возрастает (снижается), то и доходность j-ой ценной бумаги также возрастает (снижается).

Чем ближе значение ρ_ij к величине 1, тем сильнее эта взаимосвязь. Когда ρ_ij = 1, то считается, что ценные бумаги i и j имеют абсолютную положительную корреляцию: в этом случае значение годовой доходности r_i,t и r _j,t связаны положительной линейной зависимостью, то есть любым изменениям r_i,t всегда соответствуют пропорциональные изменения r _j,t в тех же направлениях.

Если ρ_ij отрицательна, то r_i,t и r _j,t имеют тенденцию изменяться в разных направлениях: когда r_i,t возрастает (снижается), r _j,t уменьшается (повышается).

Чем ближе в этом случае ρ_ij к величине (-1), тем выше степень отрицательной взаимосвязи. При ρ_ij = -1 наблюдается абсолютная отрицательная корреляция, когда r_i,t и r _j,t связаны отрицательной линейной зависимостью. При ρ_ij = 0 отсутствует какая-либо взаимосвязь между величинами доходности двух ценных бумаг. Чем ниже коэффициент корреляции ценных бумаг, составляющих портфель, тем ниже и риск инвестиционного портфеля.