Расчет сопряжения стенки резервуара с днищем
Канонические уравнения метода сил
Канонические уравнения метода сил находят широкое применение для расчета статически неопределимых систем. В этом случае за искомые неизвестные принимаются силовые факторы или реакции.
Рассмотрим этот метод на конкретном примере (рис. 4.11). Заменим исходную статически неопределимую систему на статически определимую основную систему путем удаления лишних связей.
Основную систему нагружают заданными внешними силами 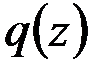 и лишними неизвестными усилиями
и лишними неизвестными усилиями 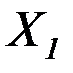 и
и 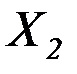 , заменяющими действие удаленных связей, в результате чего получают эквивалентную систему. При этом неизвестные усилия должны быть подобраны так, чтобы перемещения в опорах
, заменяющими действие удаленных связей, в результате чего получают эквивалентную систему. При этом неизвестные усилия должны быть подобраны так, чтобы перемещения в опорах  и
и  были такими же, как и в исходной системе.
были такими же, как и в исходной системе.
В данном примере перемещения в точках  и
и  равны нулю. Приравнивая суммарное перемещение от внешних нагрузок и неизвестных сил нулю, получим систему канонических уравнений метода сил
равны нулю. Приравнивая суммарное перемещение от внешних нагрузок и неизвестных сил нулю, получим систему канонических уравнений метода сил
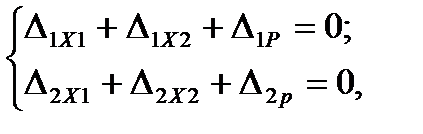 (4.25)
(4.25)
где  ,
, 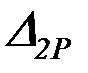 – перемещения от внешних нагрузок (рис. 4.11,в);
– перемещения от внешних нагрузок (рис. 4.11,в);
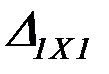 ,
, 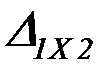 ,
, 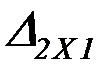 ,
, 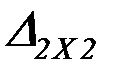 – перемещения от неизвестных сил
– перемещения от неизвестных сил
(рис. 4.11,г).
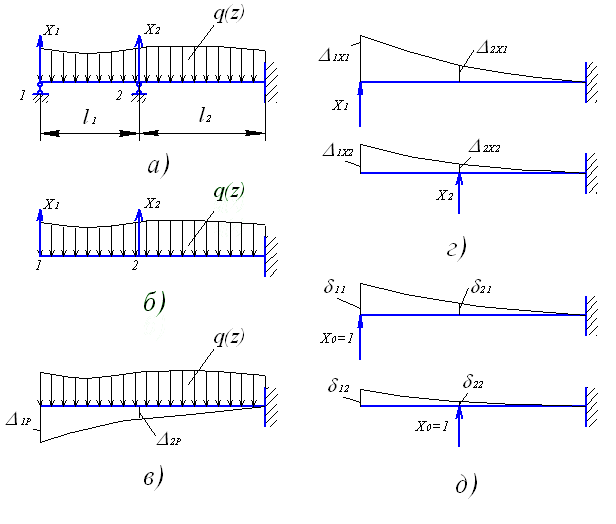
Рис. 4.11. Расчетная схема для определения реакций методом сил:
а – исходная система; б – основная система; в – перемещения от внешних нагрузок;
г – перемещения от неизвестных сил; д – перемещения от единичных сил
Если вместо неизвестных сил приложить единичные силы, то получим следующие выражения:
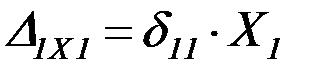 ;
; 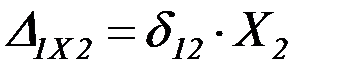 ;
;
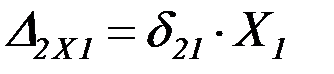 ;
; 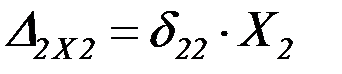 .
.
В этих выражениях 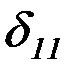 – перемещение точки
– перемещение точки  от единичной силы, приложенной вместо силы
от единичной силы, приложенной вместо силы  ;
; 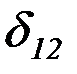 – перемещение точки
– перемещение точки  от единичной силы, приложенной вместо силы
от единичной силы, приложенной вместо силы 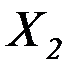 ;
;  – перемещение точки
– перемещение точки  от единичной силы, приложенной вместо силы
от единичной силы, приложенной вместо силы  ;
; 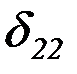 – перемещение точки
– перемещение точки  от единичной силы, приложенной вместо силы
от единичной силы, приложенной вместо силы 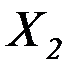 . На основании теоремы о взаимности перемещений
. На основании теоремы о взаимности перемещений
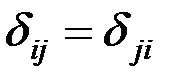 . (4.26)
. (4.26)
Таким образом, исходную задачу удалось разбить на несколько более простых, для которых решения можно найти в справочнике или воспользоваться известными из курса сопротивления материалов методами, например, методом Мора. Интеграл Мора для перемещений от внешних нагрузок и от единичных сил определяется следующим образом:
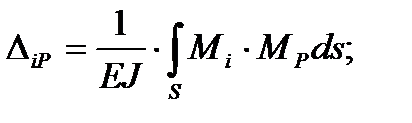
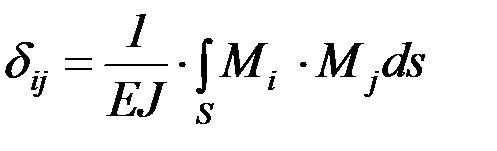 , (4.27)
, (4.27)
где 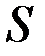 – суммарная длина всех участков;
– суммарная длина всех участков;
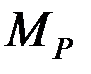 – момент от внешних нагрузок;
– момент от внешних нагрузок;
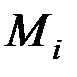 – момент от единичной силы, приложенной в
– момент от единичной силы, приложенной в 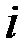 -й точке;
-й точке;
 – осевой момент инерции сечения.
– осевой момент инерции сечения.
После того, как все перемещения определены, получаем систему канонических уравнений метода сил
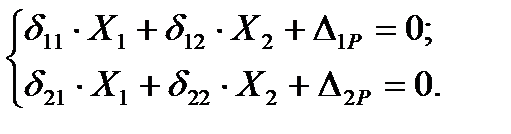 (4.28)
(4.28)
Проверочный расчет узла сопряжения стенки и днища
В зоне сопряжения стенки резервуара с днищем за счет стесненности радиальных деформаций стенки днищем возникают изгибающий момент и поперечная сила. Расчетная схема и основная система сопряжения показаны на рис. 4.12.
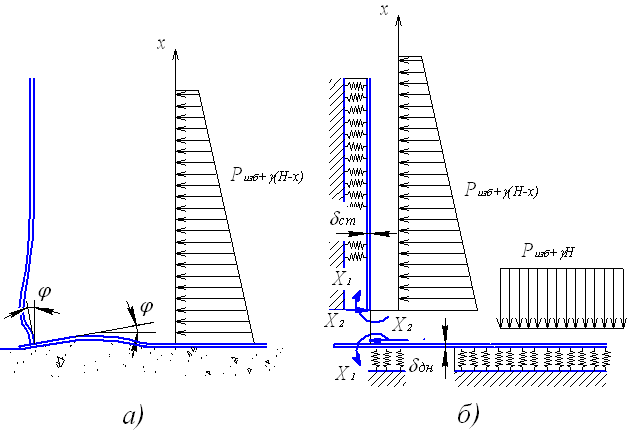
Рис. 4.12. Расчетная схема узла сопряжения стенки резервуара
и днища для метода сил: а – исходная система – совместная деформация стенки
и днища; б – основная система для расчета нижнего узла методом сил
Предполагается, что полоски единичной ширины, вырезанные из стенки и днища, работают как балки на упругом основании (по гипотезе Винклера). Основная система получается путем отрыва стенки от днища. Лишние неизвестные ( 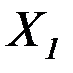 – изгибающий момент,
– изгибающий момент, 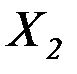 – поперечная сила) определяются методом сил из решения канонических уравнений, выражающих условие совместности перемещений тех поперечных сечений стенки и днища, в которых они жестко соединены между собой:
– поперечная сила) определяются методом сил из решения канонических уравнений, выражающих условие совместности перемещений тех поперечных сечений стенки и днища, в которых они жестко соединены между собой:
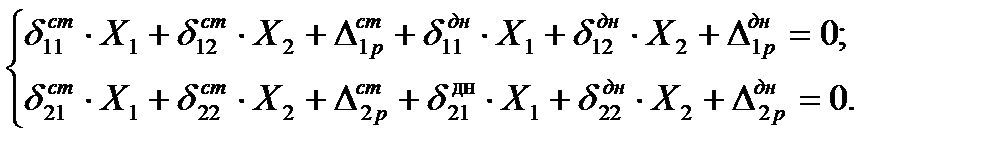 (4.29)
(4.29)
где  – перемещения от единичного момента
– перемещения от единичного момента 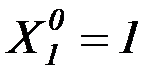 и единичной силы
и единичной силы 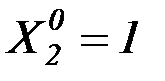 ;
;
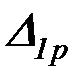 и
и 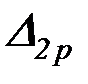 – грузовые члены, зависящие от внешних нагрузок.
– грузовые члены, зависящие от внешних нагрузок.
Для упрощения данной задачи можно считать, что днище является абсолютно жестким при его деформировании в собственной плоскости и соответственно все перемещения днища в горизонтальной плоскости от действия внешней нагрузки, момента и поперечной силы обращаются в ноль:
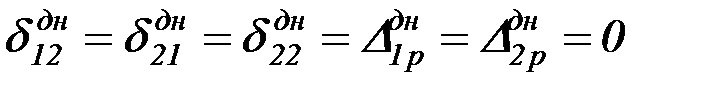 . (4.30)
. (4.30)
С учетом сделанных допущений система уравнений (4.29) принимает более простой вид:
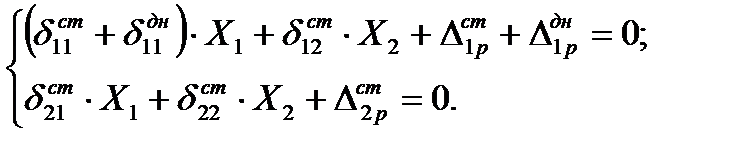 (4.31)
(4.31)
Перемещения стенки резервуара и днища, входящие в канонические уравнения, получают из решения дифференциального уравнения оси изогнутой балки на упругом основании.
Для стенки – это дифференциальное уравнение четвертого порядка
 (4.32)
(4.32)
и для днища
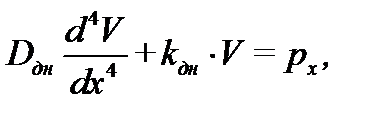 (4.33)
(4.33)
где 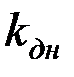 – коэффициент постели днища, зависящий от упругих свойств основания резервуара.
– коэффициент постели днища, зависящий от упругих свойств основания резервуара.
Обозначив коэффициент постели стенки как
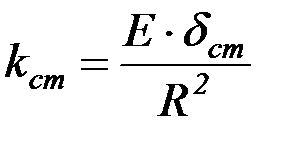
и введя нужную подстановку
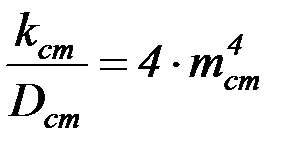 ,
,
уравнение (4.32) представляют в виде
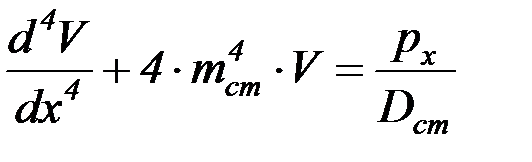 , (4.34)
, (4.34)
где 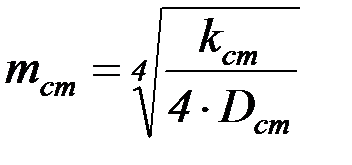 – коэффициент деформации стенки;
– коэффициент деформации стенки;
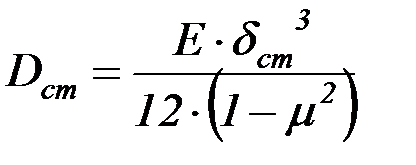 – цилиндрическая жесткость стенки;
– цилиндрическая жесткость стенки;
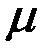 – коэффициент Пуассона;
– коэффициент Пуассона;
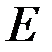 – модуль упругости стали.
– модуль упругости стали.
Аналогично преобразуется дифференциальное уравнение для днища
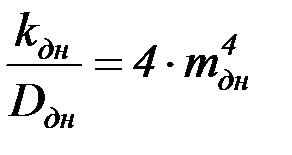 ,
,
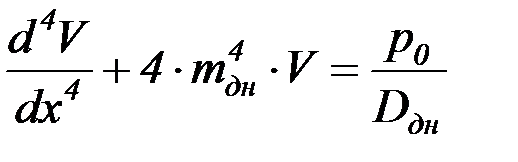 , (4.35)
, (4.35)
где 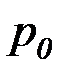 – давление в нижней точке резервуара.
– давление в нижней точке резервуара.
Для определения перемещения 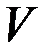 используются решения дифференциальных уравнений (4.34) и (4.35), которые имеют следующий вид
используются решения дифференциальных уравнений (4.34) и (4.35), которые имеют следующий вид

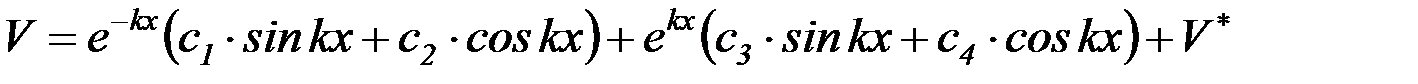 , (4.36)
, (4.36)
где 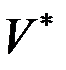 – частное решение дифференциального уравнения.
– частное решение дифференциального уравнения.
Более подробно решение для балки на упругом основании рассмотрено в учебниках по сопротивлению материалов и строительной механике. Применив эти решения для определения перемещений в стенке и днище резервуара, получают следующие соотношения:
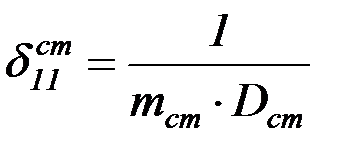 ; (4.37)
; (4.37)




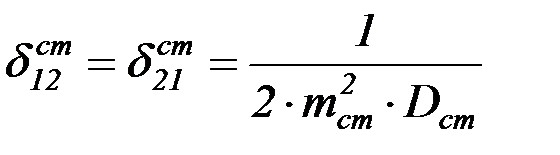 ; (4.38)
; (4.38)
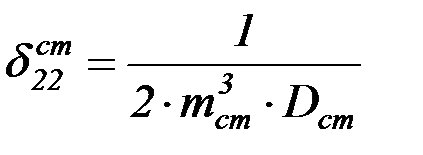 ; (4.39)
; (4.39)
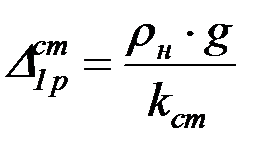 ; (4.40)
; (4.40)
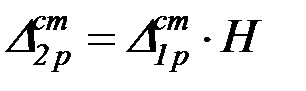 ; (4.41)
; (4.41)
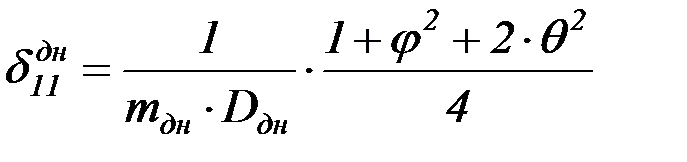 ; (4.42)
; (4.42)
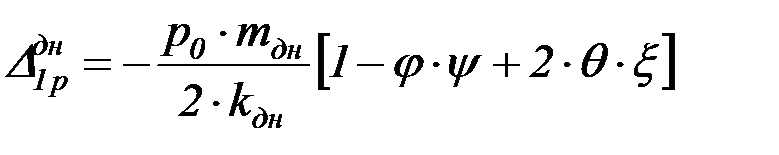 . (4.43)
. (4.43)
В этих выражениях при определении перемещений в днище используются функции Крылова:
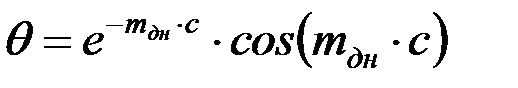 ; (4.44)
; (4.44)
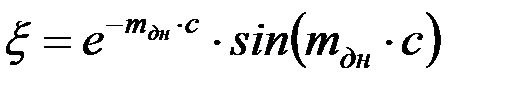 ; (4.45)
; (4.45)
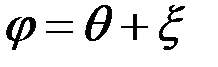 ; (4.46)
; (4.46)
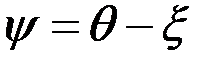 , (4.47)
, (4.47)
где 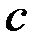 – размер свисающей части окрайки днища.
– размер свисающей части окрайки днища.
После вычисления перемещений и решения системы канонических уравнений (4.31) определяют неизвестные: изгибающий момент 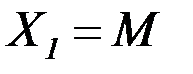 и поперечную силу в стенке резервуара
и поперечную силу в стенке резервуара 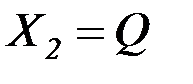 .
.
Вычислив силовые факторы в узле сопряжения, можно выполнить расчет на прочность стенки резервуара и днища, а также сварного соединения.
На рис. 4.13 изображена расчетная схема для вычисления напряжений в стенке резервуара и в днище. Предельное состояние оценивается по максимальным нормальным напряжениям, которые возникают от найденного изгибающего момента 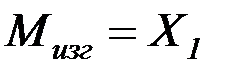 и сжимающей осевой силы
и сжимающей осевой силы 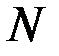 , которую вычисляли по формуле (4.14) для первого пояса стенки резервуара при проверке её на устойчивость:
, которую вычисляли по формуле (4.14) для первого пояса стенки резервуара при проверке её на устойчивость:
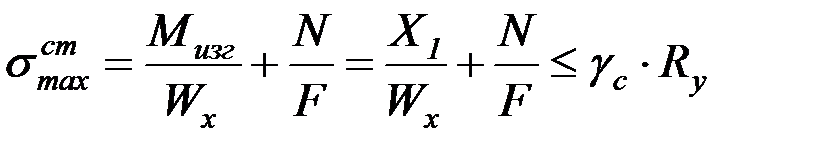 , (4.48)
, (4.48)
где  и
и 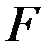 – момент сопротивления и площадь поперечного сечения стенки резервуара.
– момент сопротивления и площадь поперечного сечения стенки резервуара.
Для пластин и оболочек момент сопротивления зависит от толщины стенки 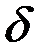 :
:
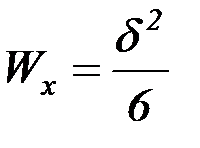 . (4.49)
. (4.49)
Формула (4.48) принимает следующий вид:
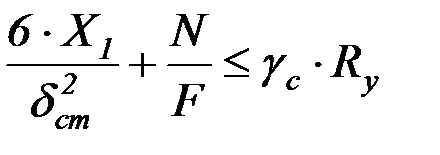 . (4.50)
. (4.50)
Днище необходимо проверить на прочность от изгибающего момента 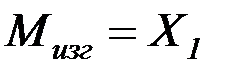 в узле сопряжения:
в узле сопряжения:
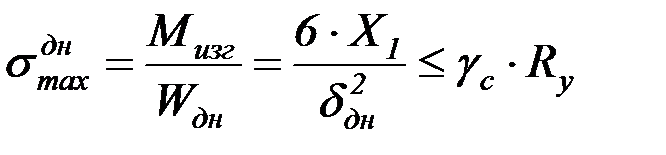 . (4.51)
. (4.51)
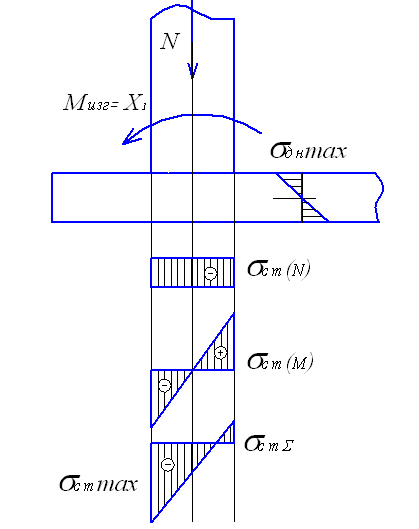
Рис. 4.13. Расчетная схема для определения нормальных напряжений
в стенке и днище
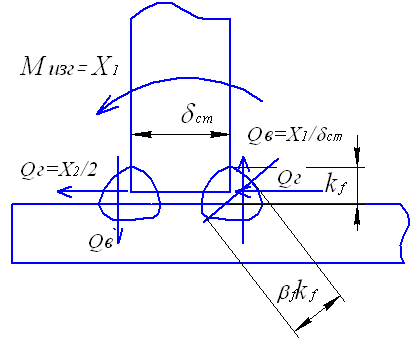
Рис. 4.14. Расчетная схема для расчета сварного шва
Стенка резервуара и днище образуют сварное тавровое соединение с угловыми швами (рис. 4.14) , расчет которого от действия продольных и поперечных сил проводят на срез по металлу сварного шва и по металлу границы сплавления.
Расчетные формулы, отражающие условие прочности сварного шва, представляют собой выражения для сдвигающих напряжений в плоскости разрушения шва. Они определяются как отношение сдвигающих усилий 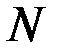 к площади сечения в плоскости среза.
к площади сечения в плоскости среза.
Расчет по металлу сварного шва:
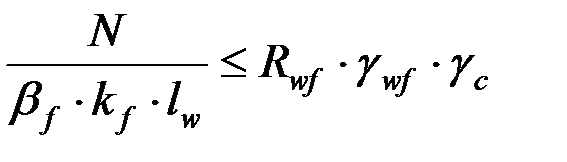 , (4.52)
, (4.52)
где 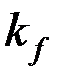 – высота катета сварного шва. Минимальный катет определяется по таблице 38 СНиП II-23-81, а максимальный не должен превышать
– высота катета сварного шва. Минимальный катет определяется по таблице 38 СНиП II-23-81, а максимальный не должен превышать
1,2 толщины более тонкой детали в соединении;
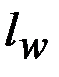 – расчетная длина шва, принимаемая меньше его полной длины;
– расчетная длина шва, принимаемая меньше его полной длины;
 – коэффициент для сталей с пределом текучести до 530 МПа, принимаемый в зависимости от вида сварки, диаметра проволоки и положения шва по таблице 34 СНиП II-23-81 (для ручной электродуговой сварки
– коэффициент для сталей с пределом текучести до 530 МПа, принимаемый в зависимости от вида сварки, диаметра проволоки и положения шва по таблице 34 СНиП II-23-81 (для ручной электродуговой сварки 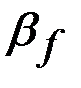 = 0,7); для сталей с пределом текучести более 530 МПа независимо от условий
= 0,7); для сталей с пределом текучести более 530 МПа независимо от условий 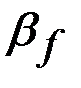 = 0,7;
= 0,7;
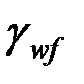 – коэффициенты условий работы шва, равные 1,0 во всех случаях, кроме конструкций, возводимых в климатических районах I1, I2, II2, II3, где
– коэффициенты условий работы шва, равные 1,0 во всех случаях, кроме конструкций, возводимых в климатических районах I1, I2, II2, II3, где 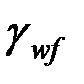 = 0,85;
= 0,85;
 – коэффициент условий работы;
– коэффициент условий работы;
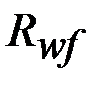 – расчетное сопротивление углового шва при расчете по металлу шва, которое принимается по таблице 56 СНиП II-23-81 в зависимости от марки электрода.
– расчетное сопротивление углового шва при расчете по металлу шва, которое принимается по таблице 56 СНиП II-23-81 в зависимости от марки электрода.
Проверку прочности углового шва, прикрепляющего стенку к днищу, производят на одновременное воздействие поперечной силы 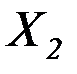 и изгибающего момента
и изгибающего момента 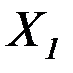 (рис. 4.14). В этом случае сдвигающая сила будет определяться как геометрическая сумма вертикальной
(рис. 4.14). В этом случае сдвигающая сила будет определяться как геометрическая сумма вертикальной 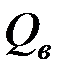 и горизонтальной
и горизонтальной 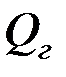 составляющих:
составляющих:
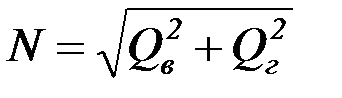 . (4.53)
. (4.53)
Вертикальная составляющая 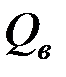 образует пару сил
образует пару сил 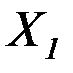 , равную произведению силы на плечо (рис. 4.14):
, равную произведению силы на плечо (рис. 4.14):
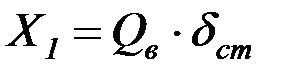 . (4.54)
. (4.54)
Горизонтальная составляющая 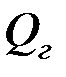 будет возникать от распределения поперечной силы
будет возникать от распределения поперечной силы 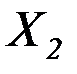 на два сварных шва:
на два сварных шва:
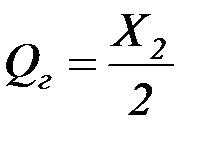 . (4.55)
. (4.55)
Подставив полученные выражения в формулу (4.53), определим расчетную нагрузку углового шва:
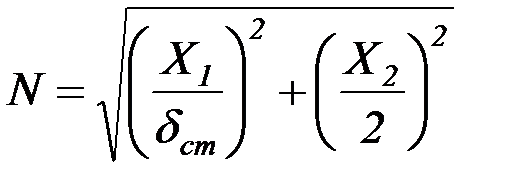 . (4.56)
. (4.56)
Необходимо напомнить, что момент 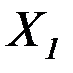 и сила
и сила 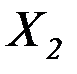 в соответствии с принятыми в теории пластин и оболочек определениями являются распределенными по ширине, т.е. отнесенными к единице длины. С учетом этого, длина сварного шва
в соответствии с принятыми в теории пластин и оболочек определениями являются распределенными по ширине, т.е. отнесенными к единице длины. С учетом этого, длина сварного шва 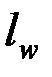 в формуле (4.52) должна равняться единице.
в формуле (4.52) должна равняться единице.
Таким образом, условие прочности сварного шва принимает следующий вид:

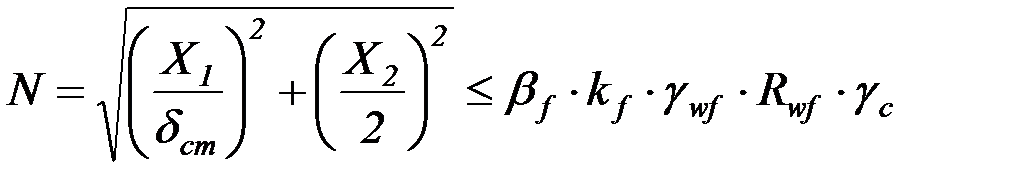 . (4.57)
. (4.57)
Аналогично выполняется расчет по границе сплавления сварного шва.
Дата добавления: 2017-05-18; просмотров: 3672;
