Расчет несущих элементов сферической крыши резервуара

Главную балку радиально-кольцевого каркаса сферической крыши вертикального резервуара на расчетной схеме (рис. 4.19) можно рассматривать как круговую арку, сопряженную на концах с опорным кольцом. Опорное кольцо устанавливается по верхнему краю цилиндрической стенки резервуара (рис. 4.17). Наиболее точные результаты будет иметь такой вариант расчетной схемы, который учитывает изгибную жесткость опорного кольца и стенки в плоскости оси арки, а также горизонтальную жесткость опорного кольца.

За счет изгибной жесткости в узле сопряжения на арку будет передаваться изгибающий момент 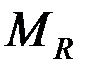, величина которого пропорциональна углу поворота опорного кольца. За счет горизонтальной радиальной жесткости опорного кольца будет возникать реактивная сила 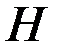, которая называется распором арки.

Рассмотрим пример расчета главной балки, в котором будем учитывать только горизонтальную жесткость верхнего опорного кольца резервуара (рис. 4.19).

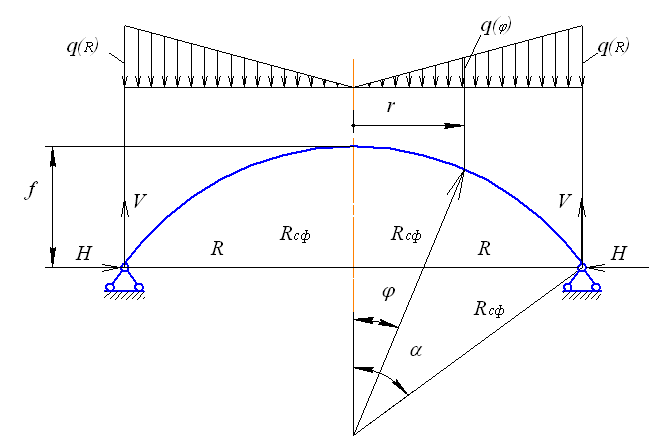
4.19. Расчетная схема главных балок каркаса сферической крыши

Арка, имеющая на концах шарнирно-неподвижные опоры, будет один раз статически неопределимой. Неизвестной реакцией является распор 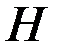, зависящий от горизонтальной жесткости опорного кольца. Чтобы определить величину распора, используется условие совместности деформаций арки и опорного кольца

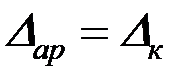, (4.58)

где 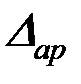– горизонтальное перемещение арки в узле сопряжения;

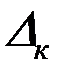– горизонтальное радиальное перемещение опорного кольца.

Для определения перемещения 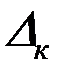воспользуемся известным решением для кольца, нагруженного равномерно распределенной погонной нагрузкой (рис. 4.20):

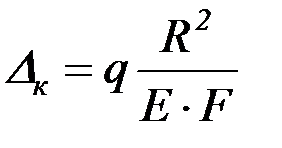, (4.59)

где 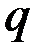– интенсивность распределенной нагрузки в плоскости кольца;

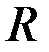– радиус кольца;

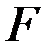– площадь сечения кольца.

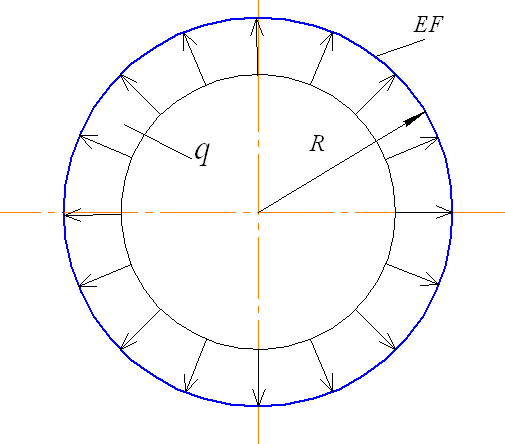
Рис. 4.20. Расчетная схема опорного кольца

Интенсивность нагрузки на кольцо 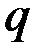необходимо выразить через распор на главные балки :

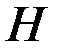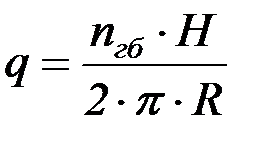, (4.60)

где 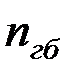– число главных балок.

Таким образом, получим горизонтальное перемещение опорного кольца

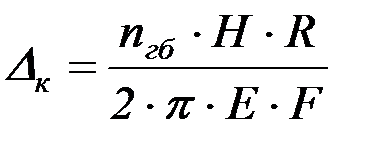. (4.61)

Для определения горизонтального перемещения в опорах арки рассмотрим расчетную схему (рис. 4.19). Для того чтобы из заданной системы получить основную систему, заменим на правом конце арки шарнирно-неподвижную опору на шарнирно-подвижную (рис. 4.21). Эквивалентную систему получим, заменив отброшенную связь неизвестной реакцией, т.е. распором 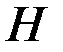. Горизонтальное перемещение опоры 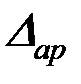определяется как сумма перемещений от заданной внешней нагрузки 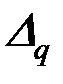(рис. 4.21,а) и неизвестного распора :

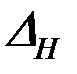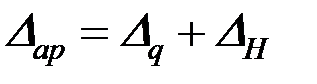(4.62)

или

,

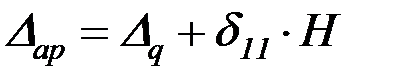где 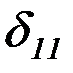– перемещение от единичной силы, приложенной вместо неизвестной силы распора 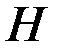(рис 4.21, б).

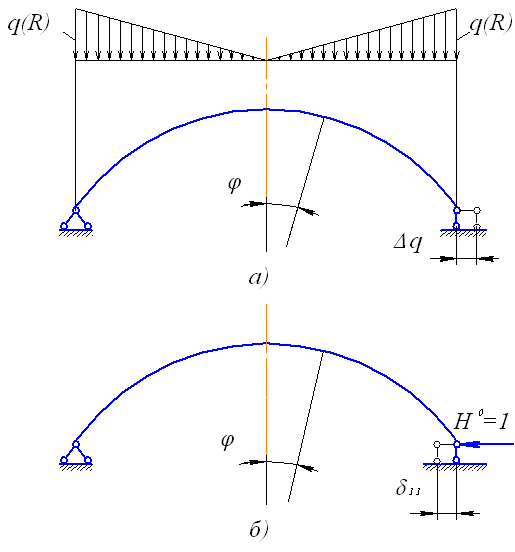
Рис. 4.21. Расчетная схема для определения перемещений
узла опирания главной балки

Перемещение 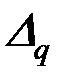можно определить, используя интеграл Мора:

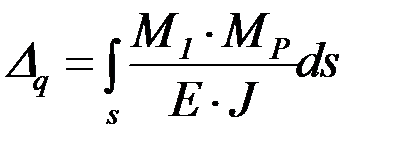, (4.63)

где 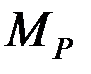– момент от внешних нагрузок;

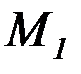– момент от единичной нагрузки.

Интеграл Мора для определения перемещения 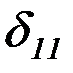получится при подстановке :

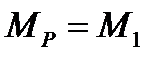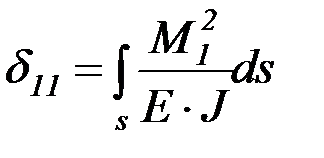. (4.64)

С учетом симметрии расчетной схемы уравнение момента от единичной силы 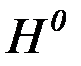(рис. 4.21, б) запишем только для правой части арки

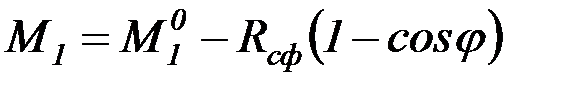. (4.65)

Тогда перемещение 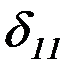с учетом выражения

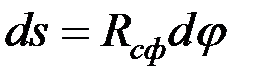
будет определяться как

.

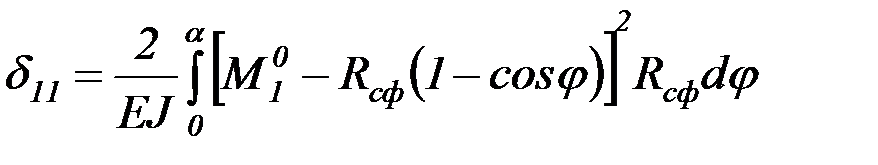Чтобы определить перемещение 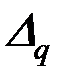, необходимо записать уравнение для изгибающего момента от внешних нагрузок

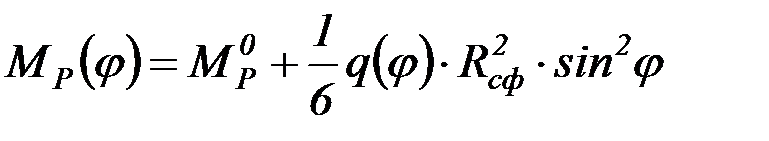, (4.66)

.

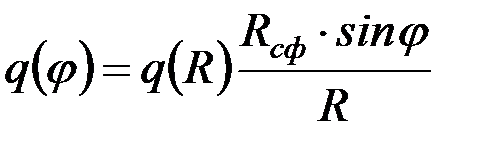Полученные выражения для моментов необходимо подставить в уравнение (4.63) и также учесть симметрию внешней нагрузки:

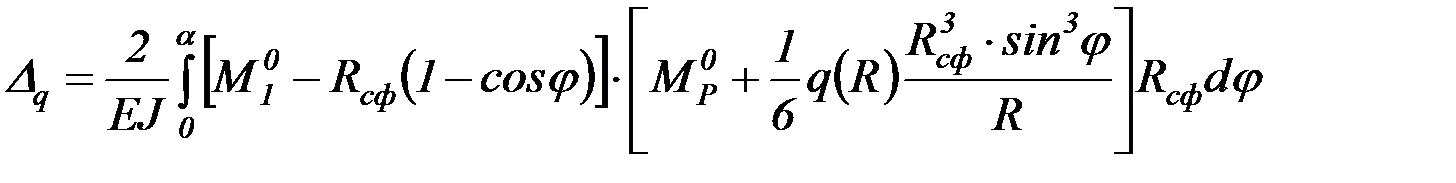, (4.67)

.

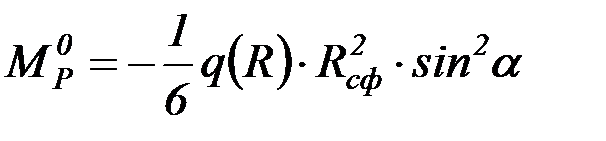После подстановки полученных выражений в уравнение (4.62) определяется распор арки :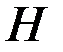

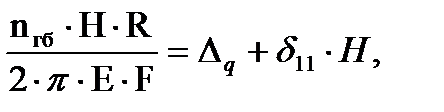
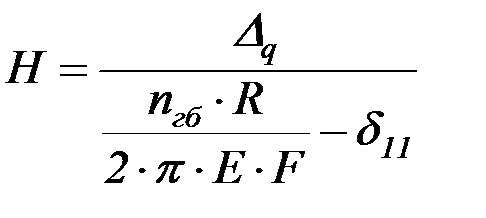. (4.68)

В приведенном ниже примере выполнения курсового проекта по дисциплине «Строительные конструкции» предложен вариант упрощенного моделирования главных балок в виде трехшарнирной арки. В этом случае получается статически определимая система и реакции опорной конструкции стенки находятся из уравнений статики. В этом примере также подробно рассмотрены проектный расчет главной балки каркасной сферической крыши, кольцевой балки настила и метод для определения толщины листа настила крыши.