Номер двутаврового сечения выбираем по ГОСТ 26020-83 «Двутавры стальные горячекатаные с параллельными гранями полок».
Двутавр № 30Б2 имеет момент сопротивления 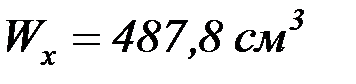 .
.
Для выполнения чертежей из ГОСТ 26020-83также выбираются все необходимые геометрические размеры.
Расчет кольцевой балки настила
В результате расчета необходимо определить размер швеллера – поперечного сечения балки настила. Наиболее нагруженной является самая длинная балка настила, при условии равномерной нагрузки на крышу.
Находим балку, наиболее удаленную от центра (рис. 4.26). Ее длину определяем по формуле
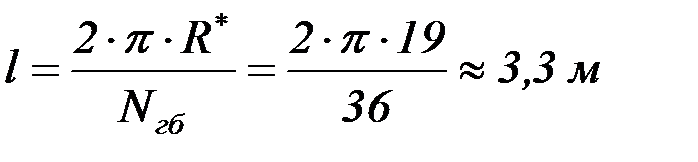 ,
,
где 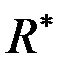 – радиус наибольшего кольца балок настила;
– радиус наибольшего кольца балок настила;
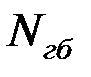 – число главных балок.
– число главных балок.
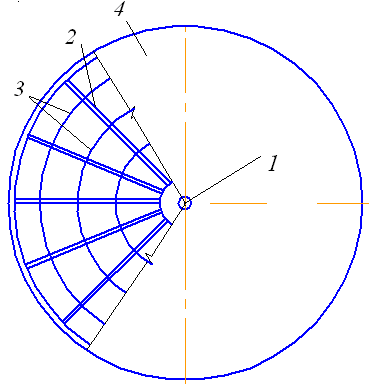
Рис. 4.26. Радиально-кольцевая конструкция сферической крыши:
1 – центральный щит; 2 – главная балка; 3 – балки настила; 4 – настил
Конструкция балки настила показана на рис. 4.27, а на рис. 4.28 – ее расчетная схема. Для определения максимального изгибающего момента необходимо определить интенсивность распределенной нагрузки:
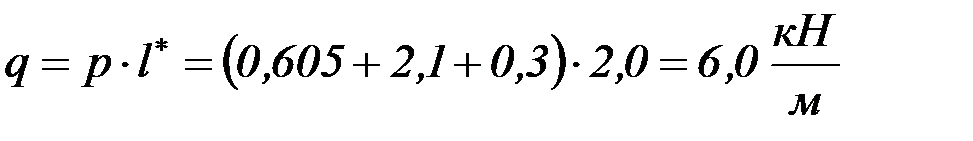 ,
,
где 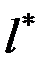 – радиальное расстояние между балками настила.
– радиальное расстояние между балками настила.
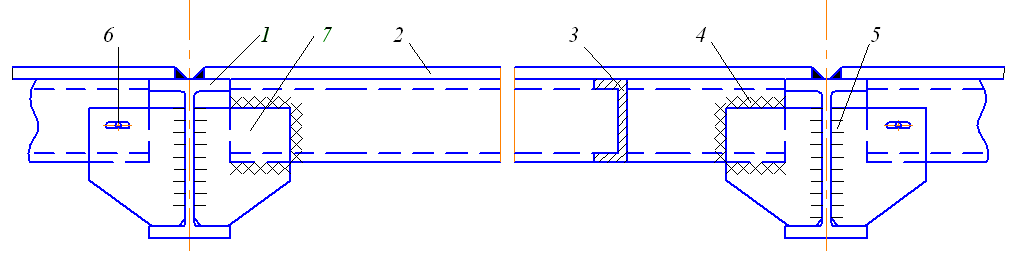
Рис. 4.27. Конструкция соединения балки настила с главными балками:
1 – двутавровая главная балка; 2 – настил; 3 – швеллер – балка настила;
4 – монтажный угловой шов; 5 – заводской угловой шов;
6 – отверстие под монтажный болт; 7 – фасонка
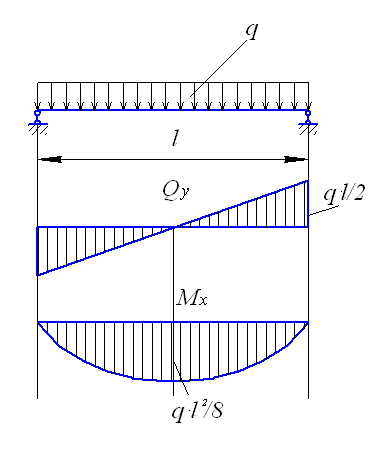
Рис. 4.28. Расчетная схема балки настила
Для выбранной расчетной схемы определяем наибольший изгибающий момент:
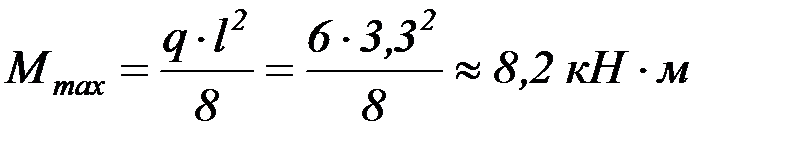 .
.
Размер поперечного сечения швеллера определяем из условия
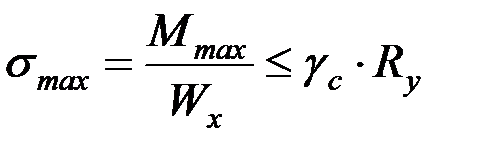 .
.
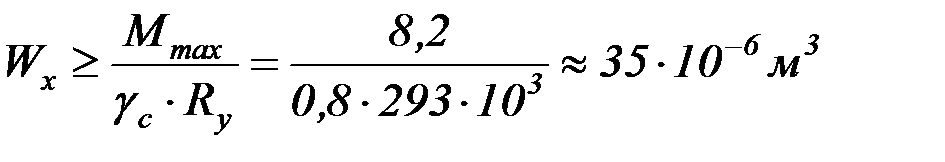 .
.
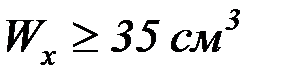 .
.
Швеллер выбираем по ГОСТ 8240: 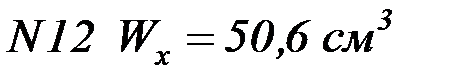 .
.
Расчет настила сферической крыши
Расчет настила производим по известному решению для прямоугольной пластины, шарнирно опертой по краям. Расчетная схема показана на рис. 4.29.
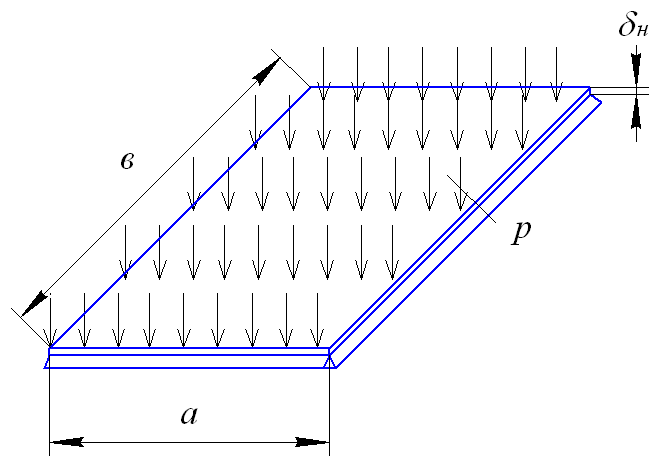
Рис. 4.29. Расчетная схема настила
При определении давления от собственного веса настила предварительно задаемся толщиной листа настила 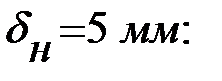
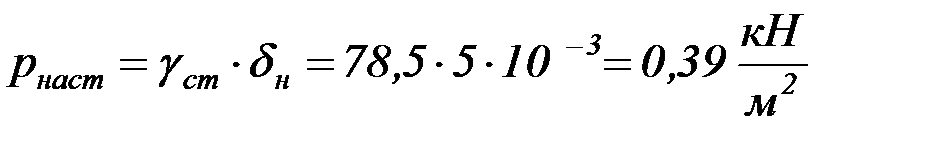 .
.
Определяем давление на пластину:
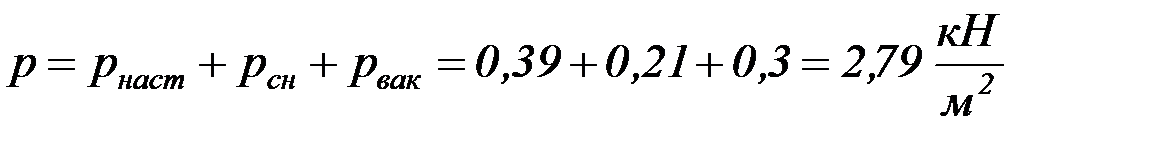 .
.
Размеры 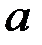 и
и 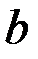 выбираются для наибольшей пластины:
выбираются для наибольшей пластины:
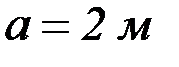 ;
; 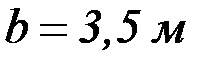 .
.
Наибольший изгибающий момент
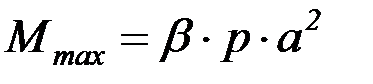 , (4.78)
, (4.78)
прогиб в центре пластины
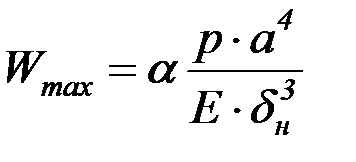 , (4.79)
, (4.79)
где 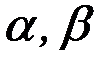 – коэффициенты, выбираемые по табл. 4.16 в зависимости от соотношения размеров пластины.
– коэффициенты, выбираемые по табл. 4.16 в зависимости от соотношения размеров пластины.
Таблица 4.16
Коэффициенты для расчета прямоугольной пластины
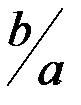
| 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 |
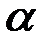
| 0,0433 | 0,0616 | 0,0770 | 0,0906 | 0,1017 | 0,1106 |
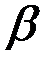
| 0,0479 | 0,0626 | 0,0753 | 0,0862 | 0,0948 | 0,1017 |
Для выбранного отношения размеров пластины 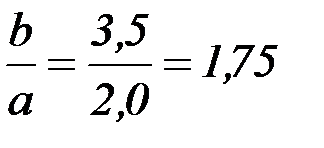 по таблице выбираем
по таблице выбираем 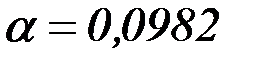 и
и 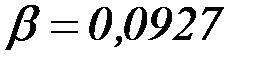 .
.
Изгибающий момент
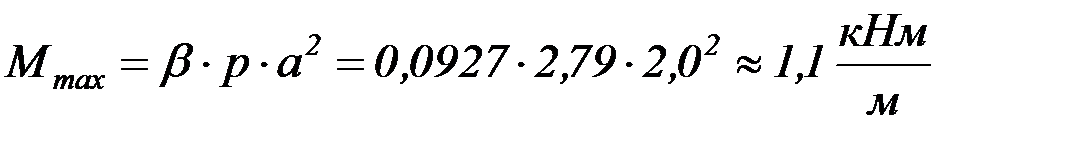 .
.
Из условия
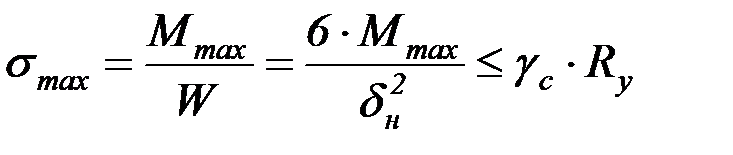
получаем
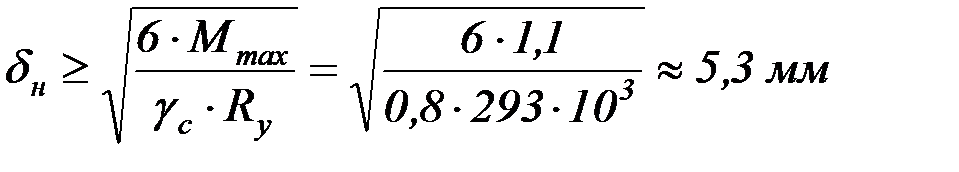 .
.
Принимаем толщину настила 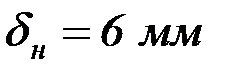 .
.
Максимальный прогиб настила
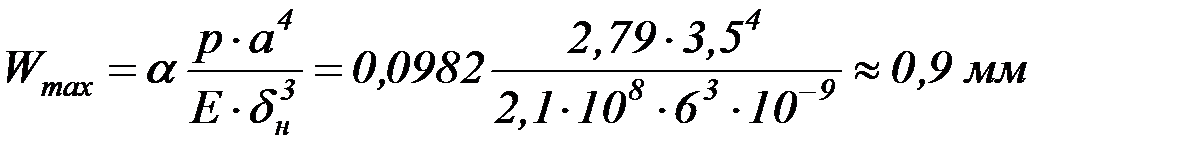 .
.
Дата добавления: 2017-05-18; просмотров: 1783;
