Пример расчета цикла
Задан цикл, состоящий из следующих процессов: 1-2 Р = const; 2-3 S=const; 3-4 υ= const; 4-1 n = 1,3; P1 = 0,1 МПа; Т1 = 338 К; Т2 = 273 К; Т3 = 433 К.
Дадим примерный вид цикла в Pυ- и TS- диаграммах (рис. 4). В Pυ – координатах построение начнем с процесса 1-2. Это изобарный процесс, идущий с уменьшением температуры, а следовательно, и с уменьшением объема. Т2 располагается левее точки 1.
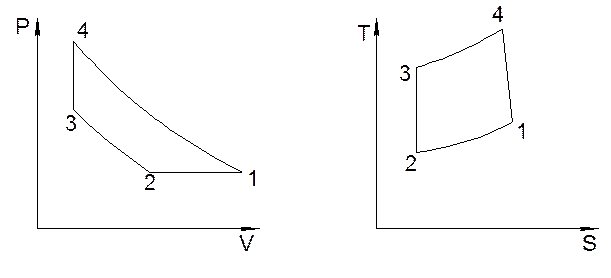
Рис. 4 . Примерное изображение цикла в Pυ – и TS – диаграммах.
2-3 – адиабатный процесс, идущий с увеличением температуры, а следовательно, с уменьшением объема (PdS = CvdT). Точка 3 располагается выше и левее т.2. 3-4 изохорный процесс, сопровождающийся ростом температуры. Точка 4 располагается выше т.3. Замыкает процесс политропа 4-1.
В TS диаграмме т.2 расположена ниже и левее точки 1, адиабата 2-3 изображается вертикальным отрезком, причем точка 3 будет расположена выше точки 1 (Т3 > Т1). Изохора 3-4 направлена от точки 3 вверх и вправо, но т. 4 должна располагаться левее точки 1, т.к. показатель 4-1 меньше показателя адиабаты. Определяем параметры состояния всех точек цикла. Из уравнения состояния найдем удельный объем воздуха в точке 1.
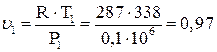 м3/кг.
м3/кг.
Удельный объем V2 равен:
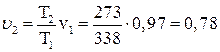 м3/кг.
м3/кг.
Используя соотношение между параметрами состояния для адиабатного процесса, определим удельный объем v3:
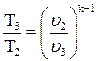 ;
; 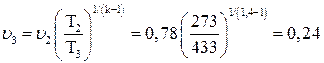 .
.
Давление Р3 равно:
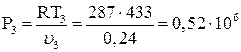 Па.
Па.
Температуру Т4 найдем из соотношения между параметрами в политропном процессе:
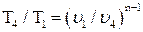 ;
; 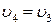 (3-4 изохора)
(3-4 изохора)
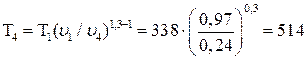 К.
К.
Давление Р4 равно:
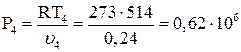 Па.
Па.
Параметры состояния сводим в таблицу 4.
Таблица 4
| Точка | Р, МПа | м3/кг | Т, К |
| 0,1 | 0,97 | ||
| 0,1 | 0,78 | ||
| 0,52 | 0,24 | ||
| 0,62 | 0,24 |
Процесс 1-2 n= 0; C = Cp = 1,025 ;
q = Cp ∙ (T2 – T1) = 1,025 ∙ (273 - 338) = -67 кДж/кг;
ΔU = Cυ ∙ (T2 – T1) = (Cp - R)∙(T2 – T1) = (1,025 – 0,287)∙(273 - 338) = -48 кДж/кг;
C υ = Cp ∙ R = 1,025 – 0,287 = 0,738 кДж/(кг∙К);
l = P∙(υ2 – υ1) = 0,1∙105 (0,78 – 0,97) = -19000 Дж/кг = -19 кДж/кг;
ΔS = Cpln(T2 / T1) = 1,025∙ln(273 / 335) = 0,22 кДж/(кг∙К);
Δh = q = -67 кДж/кг.
Процесс 2-3 n = k, C = 0.
q = 0;
ΔU = C υ (T3 – T2) = 0,738∙(433 - 273) = 119 кДж/(кг∙К);
L = -ΔU = -119 кДж/(кг∙К);
ΔS = 0;
Δh = Cp ∙ (T3 – T2) = 1,025 ∙ (433 - 273) = 166 кДж/кг;
Процесс 3-4; n = ∞; C = C υ = 0,738 кДж/(кг∙К)
q = ΔU = C υ (T4 – T3) = 0,738∙(514 - 433) = 61 кДж/кг;
l = C;
ΔS = C υ ln(T4 / T3) = 0,738 ∙ ln (514 / 433) = 0,13 кДж / (кг∙К ).
Процесс 4-1; n = 1,3; C = C υ [(n - k) / (n - 1)] = 0,738 [(1,3 – 1,4) / (1 – 1,4)] =
= - 0,22 кДж/(кг∙К);
q = C(T1 – T4) = -0,22∙(338 - 514) = 39 кДж/кг;
ΔU = C υ (T1 – T4) = 0,738 ∙ (338 - 514) = -132 кДж/кг;
l = (P4∙υ4 – P1∙ υ 1) / (n - 1) = (0,62∙0,24) –( 0,1∙0,97)∙103 / (1,3 - 1) = 170 кДж/кг;
ΔS = C∙ln (T1 / T4) = -0,22 ln(338 / 514) = 0,09 кДж/(кг∙К);
Δh = Cp (T1 – T4) = 1,025 (338 - 514) = 183 кДж/кг.
Полученные значения сводим в таблицу 5
Таблица 5
| Процессы | n | C, кДж/(кг∙К) | ΔU, кДж/кг | Δh, кДж/кг | ΔS, кДж/(кг∙К) | q, кДж/кг | l, кДж/кг |
| 1-2 | 1,025 | -48 | -67 | -0,22 | -67 | -19 | |
| 2-3 | К | -118 | |||||
| 3-4 | 0,738 | 0,13 | |||||
| 4-1 | 1,3 | -0,22 | -132 | -183 | 0,09 | ||
| Сумма |
Подведенное количество теплоты 100 кДж/кг.
Отведенное количество теплоты 67 кДж/кг.
Работа цикла 33 кДж/кг.
Термический КПД ή = l / qп = 33 / 100 = 0,33.
Изобразим цикл в PV – и TS – координатах с учетом масштаба.
В PV – диаграмме для адиабаты 2-3 и политропы 4-1 найдем координаты дополнительных точек.
m a; υa = 0,6; Pa = P2(υ2 / υa)k = 0,1(0,78 /0,6)1,4 = 0,144 МПа,
m b; υb = 0,4; Pb = 0,1(0,78 /0,4)1,4 = 0,255 МПа,
m c; υc = 0,3; Pc = 0,1(0,78 / 0,3)1,4 = 0,38 МПа,
m d; υd = 0,3 Pd = 0,1(0,97 / 0,3)1,3 = 0,46 МПа,
m e; υe = 0,4; Pe = 0,1(0,97 / 0,4)1,3 = 0,32 МПа,
m f; υf = 0,6; Pf = 0,1(0,97 / 0,6)1,3 = 0,19 МПа,
m g; υg = 0,8; Pg = 0,1(0,97 / 0,8)1,3 = 0,13 МПа.
Построим цикл в TS – диаграмме . Примем за точку отсчета энтропии нормальные условия:
T = 0 0C и Р = 1,013∙105 Па, т.к. в точке 2 Т = 273 К, Р = 1∙105 Па,
то S2 ≈ 0; S3 = S2 = 0; S4 = S3 + ΔS1-4 = 0 + 0,13 = 0,13 кДж/(кг∙К);
S4 = S3 + ΔS4-1 = 0,13 + 0,9 = 0,22 кДж/(кг∙К).
Найдем энтропию в промежуточных точках.
m a; Тa = 325 К; Sa = Cp ∙ln(T1 / Tа) = 1,025ln(325 / 273) = 0,18 кДж/(кг∙К),
m b; Тb = 300K; Sb = 1,025ln(300 / 273) = 0,1 кДж/(кг∙К),
m c; Тc = 450K; Sc = Cυ ln(Tс / T3) = 0,738ln(450 / 433) = 0,03 кДж/(кг∙К),
m d; Тd = 475K; Sd = 0,738ln(475 / 433) = 0,07 кДж/(кг∙К),
m e; Тe = 450K; Se = S +Cпол ln(Tе / T4) = 0,13+ (-0,22 ln(450 / 514)) =0,16 кДж/(кг∙К),
m f; Тf = 400K; Sf = 0,13+(-0,22ln(400 / 514)) = 0,185 кДж/(кг∙К).
Контрольные задачи
Задача 1.1. Определить, какое количество кислорода было израсходовано из баллона емкостью 40 л, если манометрическое давление в нем снизилось со 196 ат до 49 ат, а температура возросла с 27 до 37 0С. Барометрическое давление 740 мм. рт. ст.
Задача 1.2. Компрессор подает сжатый воздух в резервуар, причем за время работы компрессора давление в резервуаре повышается с атмосферного до 7 бар, а температура от 20 до 25 0С. Объем резервуара 56 м3. Барометрическое давление 745 мм.рт.ст. Определить массу воздуха, поданного компрессором в резервуар.
Задача 1.3. Поршневой компрессор всасывает в минуту 3 м3 воздуха при температуре 17 0С и барометрическом давлении В = 750 мм.рт.ст. и нагнетает его в резервуар, объем которого 8,5м3. За сколько минут компрессор поднимает давление в резервуаре до 700 кПа, если температура в нем будет оставаться постоянной? Начальное давление воздуха в резервуаре составляло 750 мм.рт.ст. при 17 0С.
Задача 1.4. В баллоне емкостью 40л находится аргон под давлением Р = 10 МПа при t = 27 0С. Определить, какое количество аргона было израсходовано из баллона, если давление в нем снизилось до 7 МПа при той же температуре? До какой температуры надо нагреть газ, чтобы при оставшемся количестве аргона восстановить начальное давление 10 МПа?
Задача 1.5. В сосуде объемом 0,5м3 находится воздух при барометрическом давлении 100 кПа и температуре 300 0С. Воздух откачивается до тех пор, пока в сосуде не образуется вакуум 600 мм.рт.ст. Температура воздуха после откачивания остается прежней. Сколько воздуха (в кг) откачано? Чему будет равно давление в сосуде, если оставшийся в нем воздух охладить до 20 0С.
Задача 1.6. При автогенное резке металлов расходуется кислород и водород. Кислород берется из баллона объемом 50 л. Давление кислорода падает с 12 МПа до 8 МПа, а температура с 30 до 17 0С. Водород расходуется из баллона объемом 40 л. Начальные его параметры Р1 = 10 МПа, t1 = 27 0С, конечные Р2 = 10 МПа, t2 = 17 0С. Определить расход кислорода на 1кг водорода.
Задача 7. Газгольдер имеет емкость V = 30 м3. Сколько килограммов водорода нужно подать в газгольдер, чтобы при t = 20 0С в нем было давление Р = 1,6 МПа (по манометру). Начальное показание манометра Р = 0,25 МПа при температуре 10 0С. Барометрическое давление 750 мм.рт.ст.
Задача 1.8. Аудитория имеет размеры 6x8x5 м. Какое количество воздуха удалится из нее при повышении температуры с t1 = 15 0C до t2 = 2 0C, если атмосферное давление В0 = 775 мм.рт.ст.
Задача 1.9. Газгольдер, объемом V = 50 м3, заполнен хлором до давления 0,8 МПа по манометру при температуре 30 0С. На технологические нужды израсходовали 200 м3 газа (объем приведен к нормальным условиям). Какое давление покажет манометр на газгольдере, если температура понизилась до 17 0 С. Барометрическое давление 0,1 МПа.
Задача 1.10. В резервуар объемом 3м3 компрессором нагнетается углекислый газ. Начальное показание манометра Р1 = 0,3ати, конечное 3 ати. Температура повышается от t1 = 45 0C до t2 = 70 0С. Определить вес подкаченного углекислого газа. Барометрическое давление 735,5 мм.рт.ст.
Задача 1.11. Какое количество воздуха в кг было израсходовано на пуск двигателя, если известно, что объем пускового баллона 200л, температура воздуха в нем перед пуском и после пуска 20 0С,давление снизилось с 23 до 19 ат.
Задача 1.12. Резервуар объемом 12 м3 заполняется углекислым газом до давления 8 ати при t = 20 0С с помощью компрессора. Компрессор засасывает в минуту 6 м3 углекислого газа при барометрическом давлении 740 мм.рт.ст. и температуре 20 0С. Найти время , в течение которого компрессор заполнит резервуар углекислотой до необходимого давления, если перед пуском компрессора в резервуаре находился углекислый газ при давлении и температуре среды.
Задача 1.13. Воздух, заключенный в баллоне емкостью 0,9 м3, выпускается в атмосферу. Температура его равна 27 0С. Определить вес израсходованного воздуха, если до его выпуска давление в баллоне составляло 9,5 МПа, после выпуска 4,2 МПа, а температура воздуха снизилась до 17 0С.
Задача 1.14. Масса газа в баллоне m = 2,9кг, давление в баллоне по манометру 4 МПа. После того, как часть газа израсходовали, давление понизилось до 1,5 МПа, температура до 10 0С. Определить массу израсходованного газа, если барометрическое давление 755 мм.рт.ст., а начальная температура газа 30 0С. R = 290 Дж/(кг∙К).
Задача 1.15. Поршневой компрессор подает 2,4м3 воздуха в минуту (объем приведен к нормальным условиям). За какое время данный компрессор сможет поднять давление воздуха в ресивере от Р1 = 0,2 МПа до Р2 = 0,8 МПа. Объем ресивера 5м3, температура воздуха 20 0С.
Задача 1.16. Для смеси газов определить: кажущуюся молекулярную массу, газовую постоянную, плотность и парциальные давления компонентов, если давление смеси Рсм , температура tсм. Состав смеси взять по первой цифре варианта, давление и температуру по второй (таблиц 6, 7)
Задача 1.17. Определить среднюю массовую и объемную теплоемкости при Р = const и V = const для смеси газов в пределах температур t1 и t2 , приняв зависимость теплоемкости от температуры линейной. Вычислить показатель адиабаты для смеси (К = Ср / Сv). Состав газа принять по первой цифре варианта (таблица), температуры t1 и t2 по второй (таблиц 6, 8 )
Таблица 6
Дата добавления: 2017-04-20; просмотров: 2759;
