Мольные теплоемкости газов, полученные на основании молекулярно-кинетической теории
Параметры состояния рабочего тела
Рабочее вещество, применяемое в различных тепловых машинах, называют рабочим телом. Свойства рабочего тела могут быть охарактеризованы набором интенсивных величин, называемых параметрами состояния. Наиболее удобными (основными) параметрами состояния являются температура, абсолютное давление и удельный объем.
Температуру, Т, измеряют по термодинамической температурной шкале. Единицей измерения температуры является Кельвин, К. Между термодинамической шкалой и шкалой Цельсия существует связь:
T = t + 273, К (1.1)
t – температура, измеренная в о С.
Единицей измерения давления в СИ является паскаль, Па или Н/м2. Соотношение между паскалем и другими единицами измерения давления:
1 Па (Н/м2) = 10-6 МПа = 10-5 бар = 750,06∙10-5 мм.рт.ст.
1 бар = 105 Па = 0,1 МПа = 1,01972 ат = 750,06 мм.рт.ст.
1 ат = 9,8067∙104 Па = 0,098067 МПа = 1 кгс/см2 = 1∙104 кгс/м2 = 735 мм.рт.ст.
1 мм.рт.ст. = 133,32 Па.
Для вычисления абсолютного давления Рабс необходимо иметь показания барометра В и манометра или вакуумметра (мановакуумметра) Ри:
Рабс = В + Ри. (1.2)
Показания манометра в формулу (1.2) следует подставлять с положительным знаком, вакуумметра – с отрицательным.
Удельный объем, υ, представляет собой объем единицы массы вещества. Это величина, обратная плотности вещества, м3/кг:
Υ = 1 / ρ = V / m, м3/кг. (1.3)
Уравнение состояния
Параметры состояния рабочего тела связаны между собой уравнением состояния:
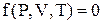
Явный вид уравнения состояния зависит от природы рабочего тела. Для идеального газа это уравнение будет иметь вид:
Для 1 кг Pυ = RT, (1.4)
Для m кг PV = mRT, (1.5)
Для n молей PV = nRμ T. (1.6)
Газовая постоянная R зависит от природы газа. Она связана с универсальной газовой постоянной Rμ формулой:
R = Rμ / M = 8314 / M. (1.7)
Температура, давление и удельный объем называются термическими свойствами вещества, а уравнения (1.4), (1.5), (1.6) – термическими уравнениями состояния.
К параметрам состояния относят также внутреннюю энергию U, Дж/кг, энтальпию h, Дж/кг, энтропию s Дж/(кг∙К). Все эти характеристики, а так же ряд других называют калорическими свойствами вещества, а уравнении вида U = f(T, P), h = φ(υ, P) калорическими уравнениями состояния.
Теплоемкость
Отношение количества теплоты dQ, полученной телом при бесконечно малом изменении его состояния, к изменению температуры тела dt называется теплоемкостью тела в данном процессе:
C = dQ / dt.
Обычно величину теплоемкости относят к единице количества вещества и в зависимости от выбранной единицы различают:
- удельную массовую теплоемкость С, отнесенную к 1 кг газа, Дж/(кг∙К);
- удельную объемную теплоемкость С′, отнесенную к количеству газа, содержащегося в 1м3 объема при нормальных физических условиях, Дж/(м3∙К);
- удельную мольную теплоемкость μС, отнесенную к одному киломолю и измеряемую в Дж/(кмоль∙К).
Зависимость между удельными теплоемкостями устанавливается очевидными соотношениями:
C=μC /M; C΄ = μC / 22,4, C΄ = ρн ∙ С. (1.8)
Здесь 22,4 м3 и ρн – объем одного киломоля и плотность газа при нормальных условиях.
Удельная теплоемкость является функцией процесса и в зависимости от его вида может изменяться в пределах -∞ < Сx < ∞. Наибольшее значение имеют удельные теплоемкости в изобарном (Р const) и изохорном (υ=const) процессах. Их обозначают соответственно:
Ср и Сυ, C′p и C′υ, μCp и μCυ.
Соотношение между теплоемкостями при постоянном давлении и постоянном объеме выражается формулой Майера:
Cp - Cυ = R или Cp - Cυ = Rμ (1.9)
Теплоемкость веществ зависит от температуры. В расчетах, связанных с определением количества теплоты, идущего на нагревание или охлаждение тела от температуры t1 до t2 пользуются средней теплоемкостью веществ в этом интервале:
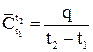 (1.10)
(1.10)
В справочной литературе приводятся значения средних теплоемкостей газов в интервале температур от 0 до t, оС. Для расчета средней теплоемкости в этом случае следует пользоваться формулой:
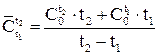 (1.11)
(1.11)
Значения истинных и средних теплоемкостей приводится в справочной литературе. В таблице I даны формулы для вычисления средних теплоемкостей некоторых газов в интервале от 0 до 1500оС. Зависимость средней теплоемкости от температуры принята линейной, типа 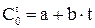 .
.
В приближенных расчетах зависимости газов от температуры можно пренебречь, приняв их за калорически идеальные. В этом случае мольные теплоемкости легко найти на основании молекулярно-кинетической теории (таблица 2).
Таблица 1
Средняя теплоемкость в пределах от 0 до 1500 оС
| Газ | Удельная массовая теплоемкость Сх, кДж/(кг∙К) | Удельная объемная теплоемкость Сх′, кДж/(м3∙К) |
| Воздух | Cυ = 0,7088 + 0,000093∙t | Cυ΄ = 0,9157 + 0,0001201∙t |
| Cp = 0,9956 + 0,000093∙t | Cp′ = 1,287 + 0,0001201∙t | |
| Н2 | Cυ = 10,12 + 0,0005945∙t | Cυ΄ = 0,9094 + 0,0000523∙t |
| Cp = 14,33 + 0,0005945∙t | Cp′ = 1,28 + 0,0000523∙t | |
| N2 | Cυ = 0,7304 + 0,00009855∙t | Cυ΄ = 0,9131 + 0,0001107∙t |
| Cp = 1,032 + 0,00009855∙t | Cp′ = 1,306 + 0,0001107∙t | |
| O2 | Cυ = 0,6594 + 0,0001065∙t | Cυ΄ = 0,943 + 0,0001577∙t |
| Cp = 0,919 + 0,0001065∙t | Cp′ = 1,313 + 0,0001577∙t | |
| CO | Cυ = 0,7331 + 0,00009681∙t | Cυ΄ = 0,9173 + 0,000121∙t |
| Cp = 1,035 + 0,00009681∙t | Cp′ = 1,291 + 0,000121∙t | |
| H2O | Cυ = 1,372 + 0,0003111∙t | Cυ΄ = 1,102 + 0,0002498∙t |
| Cp = 1,863 + 0,0003111∙t | Cp′ = 1,473 + 0,0002498∙t | |
| CO2 | Cυ = 0,6837 + 0,0002406∙t | Cυ΄ = 1,3423 + 0,0004723∙t |
| Cp = 0,8725 + 0,0002406∙t | Cp′ = 1,7132 + 0,0004723∙t |
Таблица 2
Мольные теплоемкости газов, полученные на основании молекулярно-кинетической теории
| Атомность газа | Сυ кДж/(кмоль∙К) | Ср кДж/(кмоль∙К) |
| Одноатомный | 12,5 | 20,95 |
| Двухатомный | 20,95 | 29,33 |
| Многоатомный | 29,93 | 37,71 |
Дата добавления: 2017-04-20; просмотров: 945;
