Метод узловых потенциалов

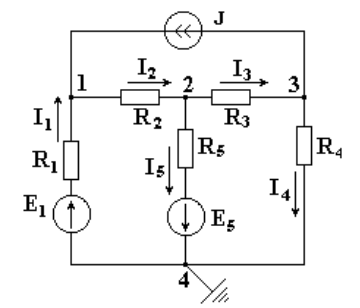Метод узловых потенциалов позволяет составить систему уравнений, по которой можно определить потенциалы всех узлов схемы. По известным разностям узловых потенциалов можно определить токи во всех ветвях. В схеме на рисунке 4.3 имеется четыре узла. Потенциал любой точки схемы можно принять равным нулю. Тогда у нас останутся неизвестными три потенциала. Узел, величину потенциала которого выбирают произвольно, называют базисным. Укажем в схеме произвольно направления токов. Примем для схемы ?4 = 0.

Рис. 4.3

Запишем уравнение по первому закону Кирхгофа для узла 1.

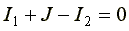(4.6)

В соответствии с законами Ома для активной и пассивной ветви

,

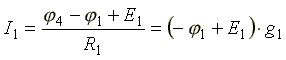где 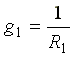- проводимость первой ветви.

,

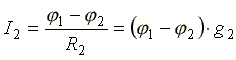где 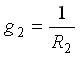- проводимость второй ветви.

Подставим выражения токов в уравнение (4.6).

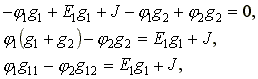(4.7)

где g11 = g1 + g2 - собственная проводимость узла 1.

Собственной проводимостью узла называется сумма проводимостей ветвей, сходящихся в данном узле.
g12 = g2 - общая проводимость между узлами 1 и 2.
Общей проводимостью называют проводимость ветви, соединяющей узлы 1 и 2.

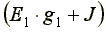- сумма токов источников, находящихся в ветвях, сходящихся в узле 1.
Если ток источника направлен к узлу, величина его записывается в правую часть уравнения со знаком "плюс", если от узла - со знаком "минус".
По аналогии запишем для узла 2:

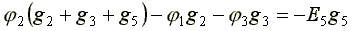(4.8)
для узла 3:

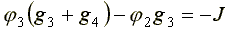(4.9)
Решив совместно уравнения (4.7), (4.8), (4.9), определим неизвестные потенциалы ?1, ?2, ?3, а затем по закону Ома для активной или пассивной ветви найдем токи.
Если число узлов схемы - n, количество уравнений по методу узловых потенциалов - (n - 1).

Замечание.

Если в какой-либо ветви содержится идеальный источник ЭДС, необходимо один из двух узлов, между которыми включена эта ветвь, выбрать в качестве базисного, тогда потенциал другого узла окажется известным и равным величине ЭДС. Количество составляемых узловых уравнений становится на одно меньше.

Метод двух узлов

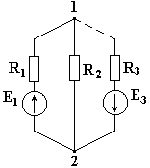Схема на рис. 4.4 имеет два узла. Потенциал точки 2 примем
равным нулю ?2 = 0. Составим узловое уравнение для узла 1.

,

,

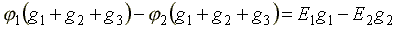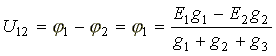Рис. 4.4

где 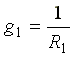, , 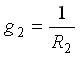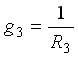- проводимости ветвей.

В общем виде:

.

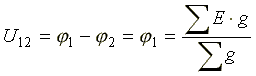В знаменателе формулы - сумма проводимостей параллельно включенных ветвей. В числителе - алгебраическая сумма произведений ЭДС источников на проводимости ветвей, в которые эти ЭДС включены. ЭДС в формуле записывается со знаком "плюс", если она направлена к узлу 1, и со знаком "минус", если направлена от узла 1.
После вычисления величины потенциала ?1 находим токи в ветвях, используя закон Ома для активной и пассивной ветви.