Основные определения
Переменным называется электрический ток, величина и направление которого изменяются во времени.
Область применения переменного тока намного шире, чем постоянного. Это объясняется тем, что напряжение переменного тока можно легко понижать или повышать с помощью трансформатора, практически в любых пределах. Переменный ток легче транспортировать на большие расстояния. Но физические процессы, происходящие в цепях переменного тока, сложнее, чем в цепях постоянного тока из-за наличия переменных магнитных и электрических полей.
Значение переменного тока в рассматриваемый момент времени называют мгновенным значением и обозначают строчной буквой i.
Мгновенный ток называется периодическим, если значения его повторяются через одинаковые промежутки времени
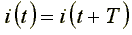
Наименьший промежуток времени, через который значения переменного тока повторяются, называется периодом.
Период T измеряется в секундах. Периодические токи, изменяющиеся по синусоидальному закону, называются синусоидальными.
Мгновенное значение синусоидального тока определяется по формуле
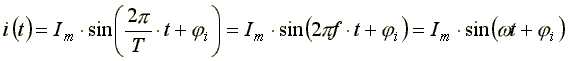
где Im - максимальное, или амплитудное, значение тока.
Аргумент синусоидальной функции 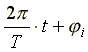 называют фазой; величину φ, равную фазе в момент времени t = 0, называют начальной фазой. Фаза измеряется в радианах или градусах. Величину, обратную периоду, называют частотой. Частота f измеряется в герцах.
называют фазой; величину φ, равную фазе в момент времени t = 0, называют начальной фазой. Фаза измеряется в радианах или градусах. Величину, обратную периоду, называют частотой. Частота f измеряется в герцах.
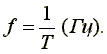
В Западном полушарии и в Японии используется переменный ток частотой 60 Гц, в Восточном полушарии - частотой 50 Гц.
Величину 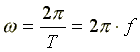 называют круговой, или угловой, частотой. Угловая частота измеряется в рад/c.
называют круговой, или угловой, частотой. Угловая частота измеряется в рад/c.
Если у синусоидальных токов начальные фазы при одинаковых частотах одинаковы, говорят, что эти токи совпадают по фазе. Если неодинаковы по фазе, говорят, что токи сдвинуты по фазе. Сдвиг фаз двух синусоидальных токов измеряется разностью начальных фаз
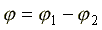
С помощью осциллографа можно измерить амплитудное значение синусоидального тока или напряжения.
Амперметры и вольтметры электромагнитной системы измеряют действующие значения переменного тока и напряжения.
Действующим значением переменного тока называется среднеквадратичное значение тока за период. Действующее значение тока (для синусоиды 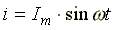 )
)
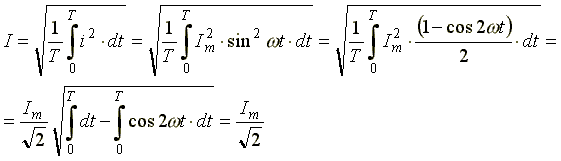 .
.
Аналогично определяются действующие значения ЭДС и напряжений
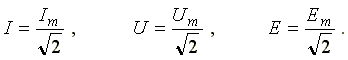 .
.
Действующие значения переменного тока, напряжения, ЭДС меньше максимальных в √2 раз.
Законы Ома и Кирхгофа справедливы для мгновенных значений токов и напряжений.
Закон Ома для мгновенных значений:
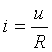 . (6.1)
. (6.1)
Законы Кирхгофа для мгновенных значений:
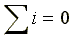 . (6.2)
. (6.2)
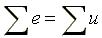 . (6.3)
. (6.3)
6.2. Изображения синусоидальных функций времени
в векторной форме
При расчете электрических цепей часто приходится складывать или вычитать величины токов или напряжений, являющиеся синусоидальными функциями времени. Графические построения или тригонометрические преобразования в этом случае могут оказаться слишком громоздкими.
Задача упрощается, если представить наши синусоидальные функции в векторной форме. Имеем синусоидальную функцию 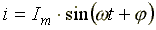 . Известно, что проекция отрезка, вращающегося вокруг оси с постоянной угловой скоростью, на любую линию, проведенную в плоскости вращения, изменяется по синусоидальному закону.
. Известно, что проекция отрезка, вращающегося вокруг оси с постоянной угловой скоростью, на любую линию, проведенную в плоскости вращения, изменяется по синусоидальному закону.
Пусть отрезок прямой длиной Im начинает вращаться вокруг оси 0 из положения, когда он образует с горизонтальной осью угол φ, и вращается против часовой стрелки с постоянной угловой скоростью ω. Проекция отрезка на вертикальную ось в начальный момент времени 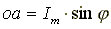 . Когда отрезок повернется на угол α1, проекция его
. Когда отрезок повернется на угол α1, проекция его 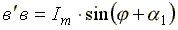 . Откладывая углы α1, α2, ... на горизонтальной оси, а проекции отрезка прямой - на вертикальной оси, получим ряд точек синусоиды (рис. 6.1).
. Откладывая углы α1, α2, ... на горизонтальной оси, а проекции отрезка прямой - на вертикальной оси, получим ряд точек синусоиды (рис. 6.1).
Пусть даны два синусоидальных тока: 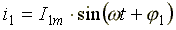 и
и
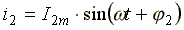 .
.
Нужно сложить эти токи и получить результирующий ток:
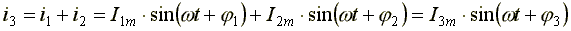
Рис. 6.1
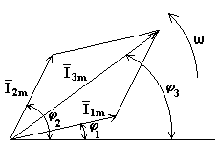
Представим синусоидальные токи i1 и i2 в виде двух радиус - векторов, длина которых равна в соответствующем масштабе I1m и I2m. Эти векторы расположены в начальный момент времени под углами φ1 и φ2 относительно горизонтальной оси. Сложим геометрически отрезки I1m и I2m. Получим отрезок, длина которого равна амплитудному значению результирующего тока I3m. Отрезок расположен под углом φ3 относительно горизонтальной оси. Все три отрезка вращаются вокруг оси 0 с постоянной угловой скоростью ω. Проекции отрезков на вертикальную ось изменяются по синусоидальному закону. Будучи остановленными для рассмотрения, данные отрезки образуют векторную диаграмму (рис. 6.2).
Векторная диаграмма - это совокупность векторов, изображающих синусоидальные напряжения, токи и ЭДС одинаковой частоты.
 Необходимо отметить, что напряжение, ток и ЭДС - это скалярные, а не векторные величины.
Необходимо отметить, что напряжение, ток и ЭДС - это скалярные, а не векторные величины.
Мы представляем их на векторной диаграмме в виде не пространственных, а временных радиус - векторов, вращающихся с одинаковой угловой скоростью.
Изображать на векторной диаграмме два вектора, вращающихся с различной угловой скоростью, бессмысленно.
Рис. 6.2
Положительным считается направление вращения векторов против часовой стрелки.
Векторные диаграммы используются для качественного анализа электрических цепей, а также при решении некоторых электротехнических задач.
6.3. Изображение синусоидальных функций времени
в комплексной форме
При расчетах цепей синусоидального тока используют символический метод расчета или метод комплексных амплитуд. В этом методе сложение двух синусоидальных токов заменяют сложением двух комплексных чисел, соответствующих этим токам.
Из курса математики известно, что комплексное число может быть записано в показательной или алгебраической форме:
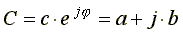
где с - модуль комплексного числа;
φ- аргумент;
a - вещественная часть комплексного числа;
b - мнимая часть;
j - мнимая единица, j = √-1.
С помощью формулы Эйлера можно перейти от показательной формы записи к алгебраической.
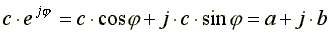
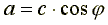
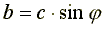
От алгебраической формы записи переходят к показательной форме с помощью формул:
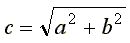
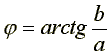
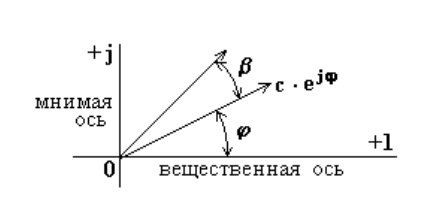
Комплексное число может быть представлено в виде радиус - вектора в комплексной плоскости. Вектор длиной, равной модулю c, расположен в начальный момент времени под углом φ относительно вещественной оси (рис.6.3).
 Умножим комплексное число на множитель
Умножим комплексное число на множитель 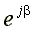 .
.
Радиус - вектор на комплексной плоскости повернется на угол β.
Множитель 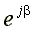 называется поворотным.
называется поворотным.
Рис.6.3
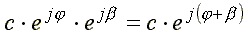
Если 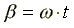 , то вектор, умноженный на
, то вектор, умноженный на 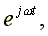 , превратится во вращающийся со скоростью ω радиус - вектор.
, превратится во вращающийся со скоростью ω радиус - вектор.
Выражение 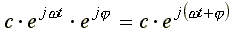 называется комплексной функцией времени.
называется комплексной функцией времени.
Применительно к напряжению, получим 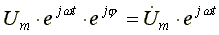 - комплексную функцию времени для напряжения.
- комплексную функцию времени для напряжения.
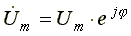 - комплексная амплитуда напряжения (исходное положение вектора в комплексной плоскости). Определим, чему равна мнимая часть комплексной функции времени для напряжения.
- комплексная амплитуда напряжения (исходное положение вектора в комплексной плоскости). Определим, чему равна мнимая часть комплексной функции времени для напряжения.
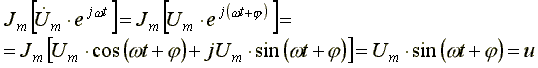
Мгновенное синусоидальное напряжение (ток, ЭДС) является мнимой частью соответствующей комплексной функции времени.
Замечание. В электротехнике над символами, изображающими комплексные напряжения, токи, ЭДС, принято ставить точку.
Синусоидальные функции времени могут быть представлены векторами в комплексной плоскости, вращающимися против часовой стрелки с постоянной угловой скоростью ω. Проекция вектора на мнимую ось изменяется по синусоидальному закону.
Пример.
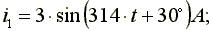
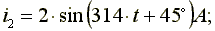
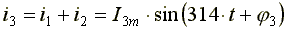
Сложение синусоидальных токов заменим сложением комплексных амплитуд, соответствующих этим токам.
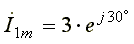
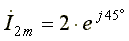
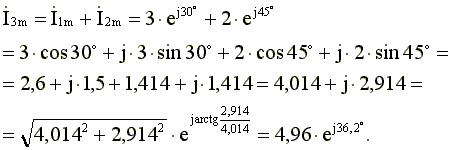
Амплитуда результирующего тока 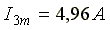 , начальная фаза -
, начальная фаза - 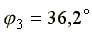 .
.
Мгновенное значение результирующего тока
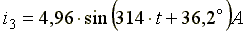 .
.
Законы Ома и Кирхгофа в комплексной форме:
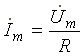 - закон Ома; (6.4)
- закон Ома; (6.4)
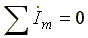 - первый закон Кирхгофа; (6.5)
- первый закон Кирхгофа; (6.5)
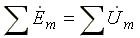 - второй закон Кирхгофа. (6.6)
- второй закон Кирхгофа. (6.6)
Лекция 7
Трехфазные цепи
Дата добавления: 2017-04-20; просмотров: 547;
