Общая характеристика переходных процессов
В электрических цепях возможны включения и отключения отдельных ветвей, короткие замыкания участков цепи, различного рода переключения. Любые изменения в электрических цепях можно представить в виде переключений или коммутаций. Характер коммутации указывается в схеме с помощью рубильника со стрелкой. По направлению стрелки можно судить, замыкается или размыкается рубильник.
При коммутации в цепи возникают переходные процессы, т.е. процессы перехода токов и напряжений от одного установившегося значения к другому.
Изменения токов и напряжений вызывают одновременное изменение энергии электрического и магнитного полей, связанных с элементами цепи - емкостями и индуктивностями. Однако энергия электрического поля и энергия магнитного поля могут изменяться только непрерывно, так как скачкообразное изменение потребовало бы от источника бесконечно большой мощности. На этом рассуждении основаны законы коммутации.
Первый закон. В любой ветви с индуктивностью ток не может изменяться скачком и в момент коммутации сохраняет то значение, которое он имел непосредственно перед моментом коммутации
iL (0+) = iL (0-),
где iL (0+) - ток в ветви с индуктивностью в момент коммутации, сразу после коммутации. Знак "+" в формуле обычно не записывается. Время переходного процесса отсчитывается от момента коммутации;
iL (0-) - ток в индуктивности непосредственно перед коммутацией.
Второй закон. Напряжение на емкости сразу после коммутации сохраняет то значение, которое оно имело непосредственно перед моментом коммутации.
uC (0+) = uC (0-),
где uC (0+) - напряжение на емкости в момент коммутации;
uC (0-) - напряжение на емкости непосредственно перед моментом коммутации.
Допущения, применяемые при анализе переходных процессов.
1. Полагают, что переходный процесс длится бесконечно большое время.
2. Считают, что замыкание и размыкание рубильника происходит мгновенно, без образования электрической дуги.
3. Принимают, что к моменту коммутации предыдущие переходные процессы в цепи закончились.
В соответствии с классическим методом расчета, переходный ток в ветви схемы представляют в виде суммы принужденного и свободного токов.
.
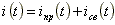где iпр(t) - принужденный ток, определяется в установившемся режиме после коммутации. Этот ток создается внешним источником питания. Если в цепь включен источник постоянной ЭДС, принужденный ток будет постоянным, если в цепи действует источник синусоидальной ЭДС, принужденный ток изменяется по периодическому, синусоидальному закону;
iсв(t) - свободный ток, определяется в схеме после коммутации, из которой исключен внешний источник питания. Свободный ток создается внутренними источниками питания: ЭДС самоиндукции индуктивности или напряжением заряженной емкости.
Свободный ток определяют по формуле:
.
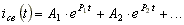Количество слагаемых в формуле равно числу реактивных элементов (индуктивностей и емкостей) в схеме.
P1, P2 - корни характеристического уравнения.
А1, А2 - постоянные интегрирования, определяются с помощью начальных условий.
Начальные условия - это переходные токи и напряжения в момент коммутации, в момент времени t, равный нулю.
Начальные условия могут быть независимыми или зависимыми.
Независимыми называют начальные условия, подчиняющиеся законам коммутации, законам постепенного, непрерывного изменения. Это напряжение на емкости uc(0) и ток в ветви с индуктивностью iL(0) в момент коммутации.
Остальные начальные условия: напряжение и ток в ветви с сопротивлением uR(0) и iR(0), напряжение на индуктивности uL(0) , ток в ветви с емкостью iC(0) - это зависимые начальные условия. Они не подчиняются законам коммутации и могут изменяться скачком.
8.2. Переходные процессы в цепях
с одним реактивным элементом
Короткое замыкание в R-L цепи
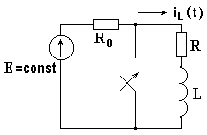
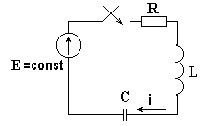
На рис. 8.1 изображена электрическая цепь, в которой включен источник постоянной ЭДС. В результате коммутации рубильник замыкается и образуется замкнутый на себя R-L контур.
До коммутации по индуктивности протекал ток
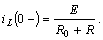
Этот ток создавал постоянное магнитное поле в индуктивной катушке.
Рис. 8.1
Определим закон изменения тока в индуктивности после коммутации.
В соответствии с классическим методом
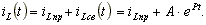
Принужденный ток после коммутации замыкается через рубильник, имеющий нулевое сопротивление, и через индуктивность не протекает. Индуктивный ток имеет только свободную составляющую
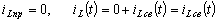
Магнитное поле, исчезая, индуктирует в индуктивной катушке ЭДС самоиндукции. Свободный ток в R-C контуре существует за счет этой электродвижущей силы.
Запишем уравнение для свободного тока в R-L контуре, используя второй закон Кирхгофа.
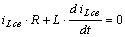(8.1)
Ищем решение этого уравнения в виде экспоненты
.
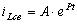Производная
.
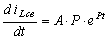Подставим значения свободного тока и производной тока в уравнение (8.1)
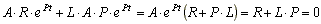(8.2)
Уравнение (8.2), полученное из уравнения (8.1), называется характеристическим.
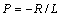- корень характеристического уравнения.
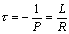- постоянная времени переходного процесса, измеряется в секундах.
Постоянная времени τ - это интервал времени, за который переходный ток уменьшается в e раз.
.
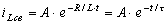Постоянную интегрирования А определяем с помощью начального условия.
В соответствии с первым законом коммутации,
.
Получим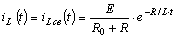 
Напряжение на индуктивности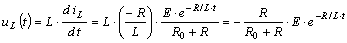 
.
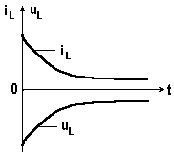На рис. 8.2 изображены кривые переходного тока в ветви с индуктивностью и переходного напряжения на индуктивности. Переходный ток и напряжение по экспоненте стремятся к нулю. В инженерных расчетах полагают, что через интервал времени, равный (4 ÷ 5)τ, переходный процесс заканчивается.
Рис. 8.2
Подключение R-L цепи к источнику постоянной ЭДС
В схеме на рис. 8.3 до коммутации рубильник разомкнут. В результате коммутации рубильник замыкается и подключает R-L цепь к источнику постоянной ЭДС. Определим закон изменения тока i(t).
.
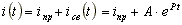Принужденный ток в установившемся режиме после коммутации
.
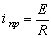В свободном режиме из схемы исключен внешний источник питания. Схема на рис. 8.3 без источника ЭДС ничем не отличается от схемы на рис. 8.1.
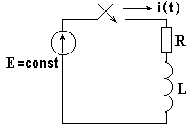Свободный ток определяется по формуле
.
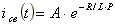Запишем значение переходного тока для момента
коммутации, (t = 0).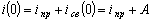 
,
откуда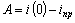 
.
Рис. 8.3
До коммутации рубильник был разомкнут, и ток в схеме отсутствовал.
Сразу после коммутации ток в индуктивности остается равным нулю.
.
.
.
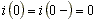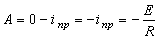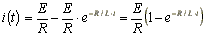Напряжение на индуктивности
.
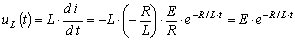На рис. 8.4 изображены кривые переходного, принужденного, свободного токов и переходного напряжения на индуктивности.
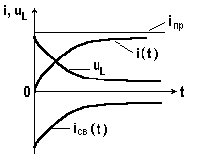Свободный ток и напряжение на индуктивности плавно уменьшаются до нуля. В момент коммутации свободный и принужденный токи одинаковы по абсолютной величине.
Переходный ток начинается при включении с нуля, затем возрастает, приближаясь к установившемуся постоянному значению.
Рис. 8.4
Короткое замыкание в R-C цепи
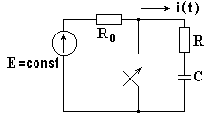
В схеме на рис. 8.5 в результате коммутации рубильник замыкается, и образуется замкнутый на себя R-C контур.
До коммутации емкость полностью зарядилась до напряжения, равного ЭДС источника питания, то есть uc(0-) = E. После коммутации емкость полностью разряжается, следовательно, принужденный ток в R-C цепи и принужденное напряжение на конденсаторе равны нулю.
В цепи существует только свободный ток за счет напряжения заряженного конденсатора.
Запишем для R-C контура уравнение по второму закону Кирхгофа
.
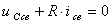Рис. 8.5
Ток через конденсатор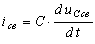 
.
Получим дифференциальное уравнение
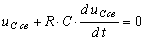. (8.3)
Решение этого уравнения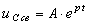 
.
Подставим значение свободного напряжения и производной от напряжения
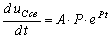в уравнение (8.3).
.
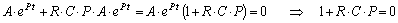Уравнение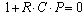 
называется характеристическим.
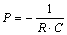- корень характеристического уравнения;
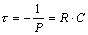- постоянная времени переходного процесса;
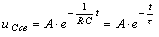
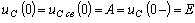
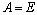
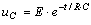
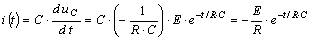
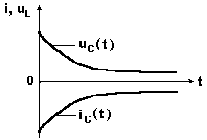Переходный ток и переходное напряжение на конденсаторе по показательному закону уменьшаются до нуля (рис. 8.6).
Рис. 8.6
Подключение R-C цепи к источнику постоянной ЭДС
Полагаем, что до коммутации конденсатор не заряжен, напряжение на нем uc(0-) = 0.
В результате коммутации рубильник замыкается, и конденсатор полностью заряжается (рис. 8.7).
Принужденное напряжение на емкости равно ЭДС источника питания ucпр= E.
Переходное напряжение
.
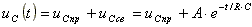В момент коммутации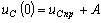 
.
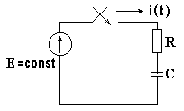Постоянная интегрирования 
.
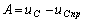В соответствии со вторым законом коммутации
. 
.
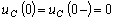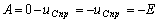Рис. 8.7
Переходное напряжение
.
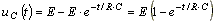Переходный ток
.
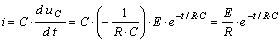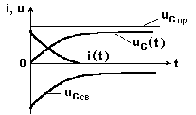Кривые напряжений и тока изображены на рис. 8.8.
Рис. 8.8
8.3. Переходные процессы в цепях
с двумя реактивными элементами
При последовательном соединении сопротивления R, катушки индуктивности L и конденсатора С образуется электрический R-L-C контур (рис. 8.9).
Дифференциальное уравнение для тока в контуре
.
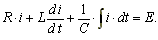После дифференцирования по t и деления на L получим
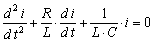. (8.4)
Решение уравнения (8.4) равно сумме принужденной и свободной составляющих
.
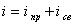В нашем случае принужденная составляющая переходного тока равна нулю, так как в схеме имеется емкость, являющаяся разрывом цепи для постоянного тока.
Рис. 8.9
Свободная составляющая является общим решением уравнения
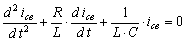. (8.5)
Пусть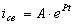 
, 
, 
.
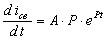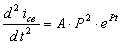После подстановки этих выражений в уравнение (8.5) получим характеристическое уравнение
.
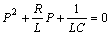Характеристическое уравнение имеет два корня
,
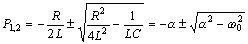где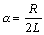 
- коэффициент затухания;
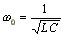- угловая резонансная частота контура без потерь.
Получим
.
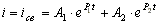Вид корней зависит от отношения
,
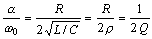где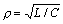 
- характеристическое или волновое сопротивление контура;
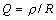- добротность контура.
Колебательный режим
Наиболее важен часто встречающийся случай, когда корни P1,2 - комплексные сопряженные с отрицательной вещественной частью, свободная составляющая имеет вид затухающих колебаний. В этом случае
, 
, 
, 
,
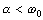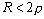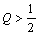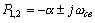где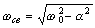 
- угловая частота собственных колебаний в контуре;
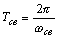- период собственных колебаний.
Ток в цепи
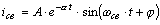, (8.6)
где А и φ - постоянные интегрирования.
До коммутации ток в индуктивности равен нулю, сразу после коммутации остается равным нулю
.
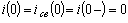Чтобы определить две постоянные интегрирования, необходимо иметь два начальных условия и составить два уравнения. Напряжение на индуктивности
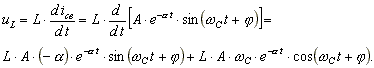. (8.7)
где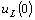 
- напряжение на индуктивности в момент коммутации, является зависимым начальным условием. Составим уравнение по второму закону Кирхгофа для момента коммутации, чтобы определить зависимое начальное условие .
.
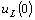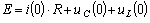До коммутации конденсатор был не заряжен, поэтому
.
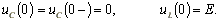Подставляя в (8.6) и (8.7) t = 0 и используя независимое и зависимое начальные условия, получим систему уравнений
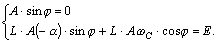(8.8)
Решив систему (8.8), определим
.
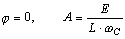
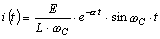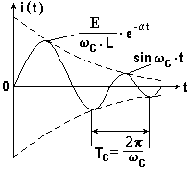На рис. 8.10 приведена кривая изменения тока в контуре при подключении к нему источника постоянной ЭДС. Из рисунка видно, что колебания в контуре затухают по показательному закону из-за потерь электрической энергии в сопротивлении R. Затухание происходит тем медленнее, чем меньше коэффициент затухания α .
Рис. 8.10
Постоянная времени переходного процесса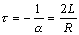 
.
При малом коэффициенте затухания величина ωС незначительно отличается от резонансной частоты ω0.
Относительное затухание колебаний характеризуется декрементом затухания, представляющим отношение мгновенных значений тока через один период.
.
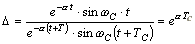Натуральный логарифм этого оператора носит название логарифмического декремента затухания
.
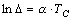Для контура с небольшим затуханием, когда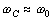 
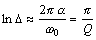
Апериодический режим в R-L-C контуре наблюдается при большом затухании, когда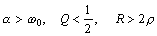 
. В этом случае корни P1,2 вещественные, отрицательные, различные.
Свободный ток определяется по формуле
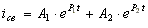. (8.9)
Напряжение на индуктивности
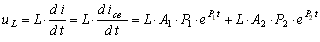. (8.10)
Подставив в уравнение (8.9) и (8.10) t = 0 и используя независимое и зависимое условия, получим систему уравнений
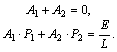
Решив эту систему, определим постоянные интегрирования
.
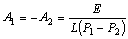Выражение для тока в контуре
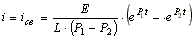
состоит из положительной, медленно затухающей экспоненты с коэффициентом затухания P1 и отрицательной, быстро затухающей экспоненты P2 (рис. 8.11).
Ток получается неколебательным, он не принимает отрицательных значений, то есть не меняет своего направления.
На границе между колебательным и апериодическим режимом при
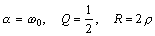
наблюдается предельный случай апериодического процесса.
Рис. 8.11
Дата добавления: 2017-04-20; просмотров: 1067;