Ное системой. Поэтому термический коэффициент полезного действия для кругового процесса

и

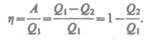(56.2)

Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении, причем если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде и в этой системе не происходит никакихизменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым.

Любой равновесный процесс является обратимым. Обратимость равновесного процесса, происходящего в системе, следует из того, что ее любое промежуточное состояние есть состояние термодинамического равновесия; для него «безразлично», идет процесс в прямом или обратном направлении. Реальные процессы сопровождают­ся диссипацией энергии (из-за трения, теплопроводности и т. д.), которая нами не обсуждается. Обратимые процессы — это идеализация реальных процессов. Их рассмот­рение важно по двум причинам: 1) многие процессы в природе и технике практически обратимы; 2) обратимые процессы являются наиболее экономичными; имеют мак­симальный термический коэффициент полезного действия, что позволяет указать пути повышения к. п. д. реальных тепловых двигателей.

§ 57. Энтропия, её статистическое толкование исвязь с термодинамической вероятностью

Понятие энтропии введено в 1865 г. Р. Клаузиусом. Для выяснения физического содержания этого понятия рассматривают отношение теплоты Q, полученной телом в изотермическом процессе, к температуре Т теплоотдающего тела, называемое приве­денным количеством теплоты.

Приведенное количество теплоты, сообщаемое телу на бесконечно малом участке процесса, равно 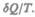Строгий теоретический анализ показывает, что приведенное

количество теплоты, сообщаемое телу в любом обратимом круговом процессе, равно нулю:

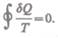(57.1)

Из равенства нулю интеграла (57.1), взятого по замкнутому контуру, следует, что подынтегральное выражение 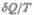есть полный дифференциал некоторой функции,