Которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние. Таким образом,
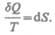(57.2)
Функция состояния, дифференциалом которой является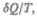 
называется энтропией
и обозначается S.
Из формулы (57.1) следует, что для обратимых процессов изменение энтропии
(57.3)
В термодинамике доказывается, что энтропия системы, совершающей необратимый цикл, возрастает:
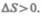(57.4) Выражения (57.3) и (57.4) относятся только к замкнутым системам, если же система
Обменивается теплотой с внешней средой, то ее энтропия может вести себя любым образом. Соотношения (57.3) и (57.4) можно представить в виде неравенства Клаузиуса
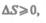(57.5)
т. е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).
Если система совершает равновесный переход из состояния 1 в состояние 2, то, согласно (57.2), изменение энтропии
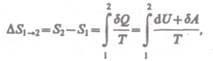(57.6)
где подынтегральное выражение и пределы интегрирования определяются через величины, характеризующие исследуемый процесс. Формула (57.6) определяет энтропию лишь с точностью до аддитивной постоянной. Физический смысл имеет не сама энтропия, а разность энтропии.
Дата добавления: 2017-04-20; просмотров: 464;