Таким образом, ускорение а есть векторная величина, равная первой производной скорости по времени.

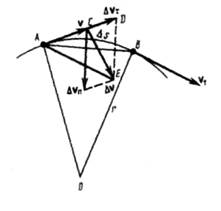
Разложим вектор 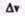на две составляющие. Для этого из точки А (рис. 4) по

направлению скорости v отложим вектор 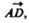по модулю равный v₁,. Очевидно, что вектор 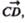равный определяет 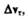изменение скорости за время по моду­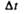

лю : 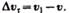Вторая же составляющая 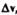, вектора 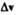характеризует изменение ско-

рости за время 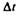по направлению.

Тангенциальная составляющая ускорения

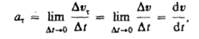
Т. е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.

Найдем вторую составляющую ускорения. Допустим, что точка В достаточно близка к точке А, поэтому 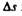можно считать дугой окружности некоторого радиуса r, мало отличающейся от хорды АВ. Тогда из подобия треугольников АОВ и EAD следует 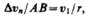но так как 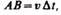то

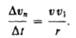
В пределе при 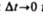получим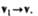

Рис.4

Поскольку 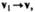угол EAD стремится к нулю, а так как треугольник EAD равнобед-

ренный, то угол ADE между 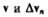стремится к прямому. Следовательно, при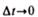

векторы 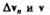оказываются взаимно перпендикулярными. Так как вектор скорости

направлен по касательной к траектории, то вектор 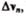перпендикулярный вектору