Свойства уравнения теории замедленного разряда.

1. 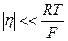. В этом случае:

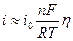(11.7)

или

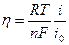(11.8)

Уравнение (11.7) следует из уравнения (11.6) при малых перенапряжениях. В этом случае соответствующая экспоненциальная зависимость примерно может быть заменена линейной, типа (11.7) из которой следует (11.8).

Из уравнения (11.7) и (11.8) следует, что при малых перенапряжениях поляризационная характеристика при замедленности стадии переноса заряда линейна, а величина

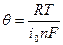(11.9)

носит название сопротивления стадии разряда - ионизации. Как видно, оно тем меньше, чем выше плотность тока обмена. При плотности тока обмена 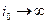мы имеем, так называемый, идеально неполяризуемый электрод, но только за счёт стадии разряда - ионизации. При 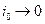электрод будет идеально поляризуемым. Потенциал такого электрода может быть смещён от равновесного значения чрезвычайно малым током.

Электроды сравнения обычно изготавливаются таким образом, чтобы при изменении плотности тока потенциал не изменялся, не отличался от своего равновесного значения, иными словами, они изготавливаются на основе систем с большими плотностями тока обмена.

На рисунке 11.1 показаны схематически системы с большими плотностями тока обмена (1) и малыми (2).

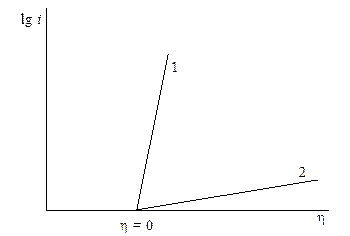
Рис. 11.1 Зависимость между плотностью тока и перенапряжением для идеально неполяризуемого (1) и идеально поляризуемого (2) электродов

2. 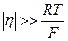В этом случае можно пренебречь скоростью обратной электрохимической реакцией, и записать:

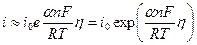(11.10)

Из (11.10) получаем:

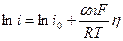, (11.11)

откуда следует, что:

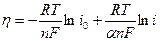(11.12)

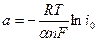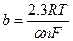Если ввести обозначения, что , а , получим, что:

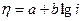(11.13)

Уравнения типа (11.13) называются уравнениями Тафеля. И.Тафель впервые в 1905г экспериментально получил зависимость (11.13) для реакции выделения водорода.

Как видно, подобная зависимость может быть следствием замедленности стадии переноса заряда. Константа b показывает насколько нужно сместить потенциал электрода, чтобы увеличить скорость реакции на порядок. Одновременно, зная коэффициент a, можно определить плотность тока обмена. Из уравнения (11.13) следует, что при замедленности стадии переноса заряда зависимость плотности тока от перенапряжения будет линейной в полулогарифмических координатах 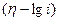. Обычно поляризационные кривые строятся именно таким образом.

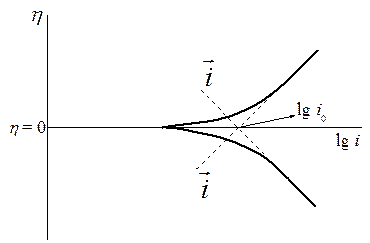
Рис. 11.2 Поляризационные кривые для стадии разряда ионизации в полулогарифмических координатах

Из рис. 11.2 видно, что плотность тока обмена можно получить экстраполяцией анодной и катодной тафелевских кривых при равновесном потенциале 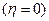. Из этого же графика видно, что скорость реакции при заданном перенапряжении будет тем больше, чем меньше наклон поляризационной кривой относительно оси перенапряжения. В пределе может быть достигнута предельная скорость процесса, не зависящая от перенапряжения. Это связано с изменением коэффициента переноса .

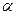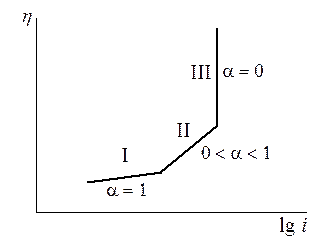
Рис. 11.3 Поляризационная кривая в широком интервале перенапряжения. I - область безбарьерного разряда, II -область обычного разряда, III -область безактивационного разряда.

Таким образом, существует три типа электродных процессов, медленной стадией которых является стадия разряда: безборьерные 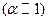, обычные 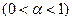и безактивационные .

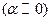Как видно из рис. 11.3, область безактивационного разряда – ионизации наблюдается при очень высоких плотностях тока. Экспериментально такие процессы не были зарегистрированы. Однако регистрация процессов с низкими значениями a была зафиксирована в экспериментах, что косвенно подтверждает возможность существования и безактивационных процессов.

В последнем случае изменением перенапряжения нельзя увеличить скорость реакции. Представление поляризационных зависимостей в форме, показанной на рис. 11.2 и рис. 11.3, на которых функцией является lg i, а аргументом перенапряжение не является общепринятым. Часто можно использовать обратную зависимость, при которой функцией является перенапряжение, а аргументом lg i. Как правило, выбор подобных зависимостей определяется тем, что задаётся в эксперименте: плотность тока или перенапряжение, т.е какой метод используется: потенциостатический (потенциодинамический) или гальваностатический (гальванодинамический).