Форма поляризационной кривой при наличии стадии массопереноса.

Учитывая, что перенапряжение (h) есть не что иное, как:

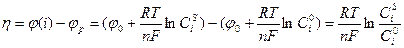, (10.10)

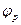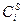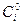где - равновесный потенциал, а отношение к можно представить, исходя из:

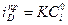(10.11)

в то время как:

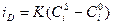(10.12)

тогда, используя уравнения (10.11) и (10.12) можно записать, что:

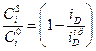, (10.13)

откуда, следует, что

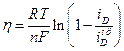(10.14)

Мы получили взаимосвязь между перенапряжением и плотностью диффузионного тока, т.е. форму поляризационной кривой в условиях замедленности стадии массопереноса (рис. 10.3).

Эта зависимость имеет вид:

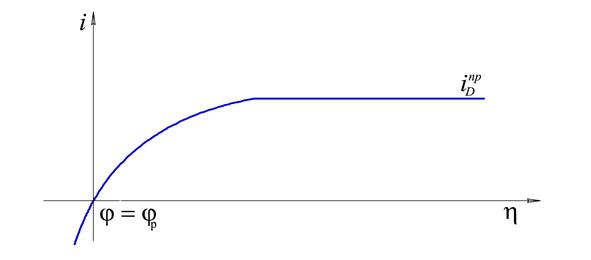
Рис. 10.3 Поляризационная кривая при замедленности стадии массопереноса ( 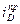-предель­ный диффузионный ток (предельная плотность диффузионного тока))

Величина 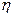при достижении предельного тока (перенапряжения) стремится к бесконечности. Это видно из (10.14): при 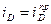выражение в скобках становится равным 0,а h ® ¥. Согласно В.Нернсту величина 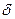не может быть рассчитана, а используется как некая фиктивная величина. Известно только то, что она зависит от скорости перемешивания, уменьшаясь с увеличением последней. Следовательно, и предельный ток диффузии должен зависеть от скорости перемешивания.

В настоящее время существует ряд гидродинамических систем, для, которых величина предельного тока (предельной плотности тока) может быть рассчитана. Такой системой является вращающийся дисковый электрод, который представляет собой торец цилиндра, помещённого в электролит, боковая поверхность которого покрыта изолятором. Этот электрод вращается в жидкости с определённой угловой скоростью 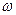(рис. 10.4).

Теория вращения дискового электрода была разработана В.Г. Левичем. Величина диффузионного тока по В.Г. Левичу определяется следующим уравнением:

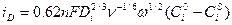, (10.15)

где 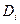- коэффициент диффузии; 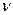- кинематическая вязкость раствора; 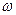- угловая частота вращения диска.

Очевидно, что:

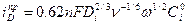(10.16)

Из уравнения (10.16) видно, что для вращающегося дискового электрода:

1. величина предельного диффузионного тока может быть рассчитана;
2. она пропорциональна квадратному корню из частоты вращения 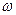(рис. 10.5);
3. она пропорциональна концентрации электрохимически активного иона;
4. на основании (10.16) может быть рассчитана величина К в уравнении (10.11) и (10.12)
5. при известной вязкости и концентрации может быть рассчитан коэффициент диффузии; 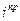не зависит от размеров диска; такие поверхности носят название равнодоступных в диффузионном отношении поверхностей.

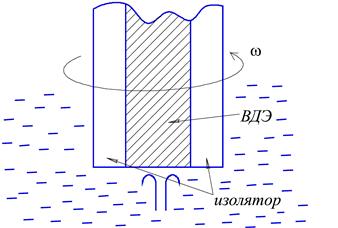
Рис. 10.4 Схема вращающегося дискового электрода

С помощью вращающегося дискового электрода можно определить составляющие тока, которые не зависят от диффузии, т.е. изучать кинетику электрохимических реакций.

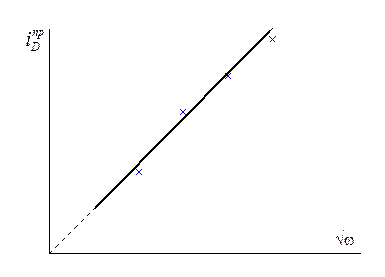
Рис. 10.5 Зависимость предельного диффузного тока от частоты вращения.

Если бы можно было достичь бесконечно большой скорости вращения, то тогда появилась бы возможность полностью ликвидировать концентрационные ограничения. Чисто математически эту проблему можно решить, построив зависимость обратных величин плотности тока от Öw и экстраполируя ток (плотность тока) на бесконечно большую скорость вращения (см. рис. 10.6).

Учитывая, что:

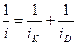(10.17)

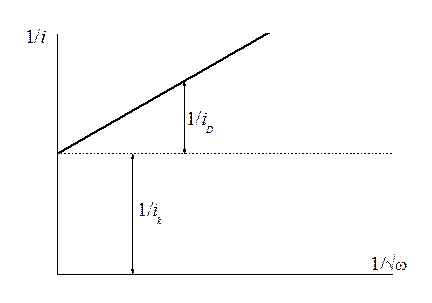
Рис. 10.6 Метод обработки экспериментальных данных, позволяющий выделить кинетический ток экстраполяцией диффузионного тока на бесконечно большую скорость вращения.

Вращающийся дисковый электрод не является единственной системой с равнодоступной поверхностью. Другими такими системами являются: электрод в ячейке с механическим перемешиванием, расположенный непосредственно под мешалкой, электрод в окрестности точки набегания, расположенный на поверхности обтекаемого шара, диска, вращающийся цилиндрический электрод и др.

В общем случае толщина диффузионного слоя зависит от размеров электрода, поскольку толщина диффузионного пограничного слоя 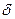зависит от толщины гидродинамического пограничного слоя, который иногда называют слоем Прандтля. Гидродинамический пограничный слой – это такой слой, в котором происходит изменение скорости течения жидкости от нулевой (непосредственно на поверхности тела) до постоянной в объёме электролита (см. рис 10.7).

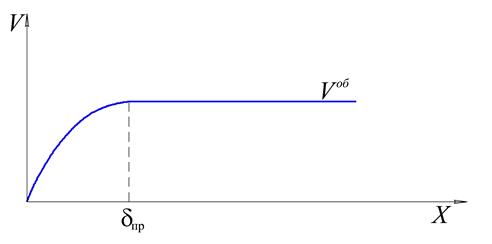
Рис. 10.7 Изменение скорости течения жидкости по мере приближения к твёрдому телу, где ( 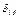-гидродинамический пограничный слой, x – расстояние от поверхности электрода)

В обычных жидкостях

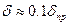(10.18)

Уравнение (10.18) соблюдается в тех случаях, когда безразмерный критерий (число Шмидта) Sc = 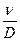~ 10³.

Именно такие величины Sc наблюдаются в обычных жидкостях, и в этих условиях выполняется соотношение (10.18).

Если число Шмидта ~ 1, то

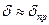, (10.19)

т.е. диффузионный пограничный слой численно равен гидродинамическому пограничному слою. Таким образом, в обычных жидкостях наблюдается следующая структура пограничных слоев:

1. гидродинамический пограничный слой;
2. диффузионный пограничный слой;
3. диффузная часть двойного слоя;
4. плотная часть двойного слоя.

Известно, что течение жидкости может быть, как ламинарным, так и турбулентным. В последнем случае в жидкости всегда наблюдаются флуктуации скорости течения, а, следовательно, флуктуации диффузионного пограничного слоя .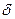

Совершенно очевидно, что в таком случае предельный ток будет колебаться вокруг некоторого среднего значения, что связано с колебаниями толщины .

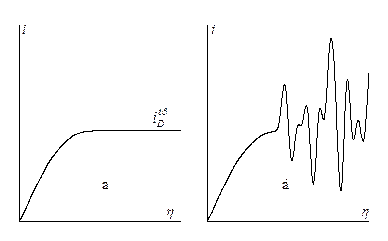
Рис. 10.8 Поляризационные кривые при ламинарном (а) и турбулентном (б) течении раствора в условиях замедленности стадии массопереноса

Как видно из рис. 10.8 на предельном токе наблюдаются пульсации плотности тока, что связано с пульсацией d.